6.
Элементарные преобразования матрицы
Определение. Элементарными преобразованиями матрицы назовем следующие преобразования:
1) умножение строки на число, отличное от нуля;
2) прибавление к элемнтам одной строки элементов другой строки;
3) перестановка строк;
4) вычеркивание (удаление) одной из одинаковых строк (столбцов);
5) транспонирование;
Те же операции, применяемые для столбцов, также называются элементарными преобразованиями.
С помощью элементарных преобразований можно к какой-либо строке или столбцу прибавить линейную комбинацию остальных строк ( столбцов ).
Алгоритм метода Жордана-Гаусса
Алгоритм решения систем уравнений методом Жордана-Гаусса состоит из ряда однотипных шагов, на каждом из которых производятся действия в следующем порядке:
Проверяется, не является ли система несовместной. Если система содержит противоречивое уравнение, то она несовместна.
Проверяется возможность сокращения числа уравнений. Если в системе содержится тривиальное уравнение, его вычеркивают.
Если система уравнений является разрешенной, то записывают общее решение системы и если необходимо — частные решения.
Если система не является разрешенной, то в уравнении, не содержащем разрешенной неизвестной, выбирают разрешающий элемент и производят преобразование Жордана с этим элементом.
Далее заново переходят к пункту 1
Пример 3 Решить систему уравнений методом Жордана-Гаусса.
Найти: два общих и два соответствующих базисных решения
Решение:
Вычисления приведены в нижеследующей таблице:
Справа от таблицы изображены действия над уравнениями. Стрелками показано к какому уравнению прибавляется уравнение с разрешающим элементом, умноженное на подходящий множитель.
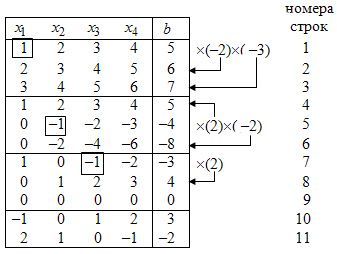
В первых трех строках таблицы помещены коэффициенты при неизвестных и правые части исходной системы. Результаты первого преобразования Жордана с разрешающим элементом равным единице приведены в строках 4, 5, 6. Результаты второго преобразования Жордана с разрешающим элементом равным (-1) приведены в строках 7, 8, 9. Так как третье уравнение является тривиальным, то его можно не учитывать.
Равносильная система с разрешенными
неизвестными
и
имеет
вид:
Теперь можем записать Общее решение:
Приравниваем свободные переменные
и
нулю
и получаем:
.
Базисное решение:
Для того чтобы найти второе общее и
соответствующее ему базисное решение,
в полученной разрешенной системе в
каком-либо уравнении необходимо выбрать
какой-либо другой разрешающий элемент.
(дело в том, что линейное уравнение может
содержать несколько общих и базисных
решений). Если разрешенная система
уравнений, равносильная исходной системе
содержит
неизвестных
и
уравнений,
то число общих и соответствующих базисных
решений исходной системы равно числу
сочетаний
и
.
Количество сочетаний можно вычислить
по формуле:
В нашем случае выбран разрешающий элемент (-1) в первом уравнении при (строка 7). Далее производим преобразование Жордана. Получаем новую разрешенную систему (строки 10,11) c новыми разрешенными неизвестными и :
Записываем второе общее решение:
И соответствующее ему базисное
решение:
Ответы:
Общее решение:
Базисное решение:
Общее решение:
Базисное решение:
7.
Вектор
Вектор (от лат. vector, буквально — несущий, перевозящий), в геометрическом смысле — направленный отрезок, то есть отрезок, у которого указаны начало (называемое также точкой приложения В.) и конец.