
- •1.Комплексные числа (геометрическое представление, алгебраическая, тригонометрическая и показательная форма записи). Действия с комплексными числами.
- •2.Вещественные числа. Точная верхняя и точная нижняя грань. Числовые последовательности. Сходящиеся последовательности.
- •3. Свойства бесконечно малых последовательностей.
- •4.Свойства произвольных сходящихся последовательностей. Сходящиеся в несобственном смысле последовательности. Монотонные последовательности. Число е. Теорема о стягивающихся сегментах.
- •5.Предельные точки последовательности. Верхний и нижний пределы последовательности. Теорема Больцано-Вейерштрасса.
- •6. Фундаментальные последовательности. Критерий Коши сходимости числовой последовательности.
- •Критерий Коши.
- •7. Понятие функции. Предельное значение функции (по Коши и по Гейне)
- •8. Критерий Коши существования предельного значения функции в точке.
- •9. Первый и второй замечательный пределы. Таблица эквивалентности. Свойства пределов функции в точке, связанные с арифметическими операциями, с непавенствами.
- •10. Бесконечно малые и бесконечно большие функции. Эквивалентность, порядок малости, порядок роста.
- •11. Классификация точек разрыва. Примеры.
- •12.Понятие производной, дифференцируемости, первого дифференциала функции независимого аргумента.
- •13. Свойства функций, непрерывных на отрезке (локальная ограниченность, прохождение через 0, промежуточные значения).
- •20. Правило дифференцирования сложной функции и функции заданной параметрически.
- •21.Первый дифференциал. Свойства.
- •22.Производные и дифференциалы высших порядков. Формула Лейбница.
- •23.Правило Лопиталя.
- •24.Ряд Тейлора. Остаточный член в ряде Тейлора в разных формах.
- •25.Ряд Маклорена для элементарных функций.
- •26.Участки монотонности функции, точки экстремума. Необходимое условие экстремума.
- •27.Первое и второе достаточное условие экстремума.
- •28.Выпуклость вверх и вниз. Точки перегиба. Необходимое условие существования точек перегиба.
- •29.Два достаточных условия существования точки перегиба.
- •31.Вертикальные и наклонные асимптоты. Полное исследование графика функции.
- •32.Понятие первообразной функции и неопределенного интеграла. Основные свойства неопределённого интеграла.
1.Комплексные числа (геометрическое представление, алгебраическая, тригонометрическая и показательная форма записи). Действия с комплексными числами.
Комплексным
числом z называется
упорядоченная пара действительных
чисел x и y.
Первое
из них x называется
действительной частью комплексного
числа z и
обозначается Rez, x =
Rez;
второе
число y называется
мнимой частью комплексного числа z и
обозначается Imz, y =
Imz.
Два
комплексных числа равны тогда и только
тогда, когда равны их действительные и
мнимые части:
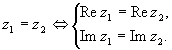
Алгебраическая форма записи комплексного числа
![]()
Число
![]()
![]() ,
где
,
где ![]() называется
комплексно сопряженным числу
называется
комплексно сопряженным числу
![]()
![]()
Комплексное число z = x + iy естественно изображать в виде точки на плоскости с декартовыми координатами (x, y).
Если x и y - декартовы координаты точки плоскости, то, перейдя на плоскости к полярным координатам (r, j) и воспользовавшись связью x = rcosj, y = rsinj получим тригонометрическую форму записи комплексного числа: z = r (cosj + isinj) . При этом число r называют модулем комплексного числа, |z| = r, а число j - аргументомкомплексного числа, Arg z = arg z+2kp= j.
При
решении задач для вычисления аргумента
удобно пользовааться схемой, приведенной
ниже:
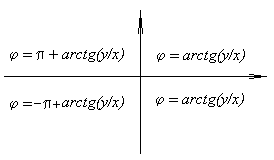
Справедливы
соотношения:
![]()
Используя
формулу Эйлера
![]() получим показательную
форму записи
комплексного числа:
получим показательную
форму записи
комплексного числа:
![]()
2.Вещественные числа. Точная верхняя и точная нижняя грань. Числовые последовательности. Сходящиеся последовательности.
Пусть X-числовое множество, содержащее хотя бы одно число (непустое множество).
x X - x содержится в Х. ; x X - x не принадлежит Х.
Определение: Множество Х называется ограниченным сверху (снизу), если существует число М(m) такое, что для любого x X выполняется неравенство x M (x m), при этом число М называется верхней(нижней) гранью множества Х. Множество Х называется ограниченным сверху, если M, x Х x M. Определение неограниченного сверху множества. Множество X называется неограниченным сверху, если M x Х x M. Определение множество X называется огранич., если оно ограничено сверху и снизу, то есть М, m такие, что x Х m x M. Эквивалентное определение огр мн-ва: Множество X называется ограниченным, если A > 0, x X: x A. Определение: Наименьшая из верхних граней ограниченного сверху множества Х называется его точной верхней гранью, и обозначается SupХ
(супремум).
![]() =SupХ.
Аналогично можно определить точную
=SupХ.
Аналогично можно определить точную
нижнюю грань. Эквивалентное определение точной верхней грани:
Число![]() называется
точной верхней гранью множества Х,
если: 1)
x
X:
х
(это условие показывает, что
-
одна из верхних граней). 2)
называется
точной верхней гранью множества Х,
если: 1)
x
X:
х
(это условие показывает, что
-
одна из верхних граней). 2)![]() <
x
X:
х
>
(это условие показывает, что
-
<
x
X:
х
>
(это условие показывает, что
-
наименьшая из верхних граней).
Sup X= :
x X: x .
 <
x
X:
x
>
.
<
x
X:
x
>
.
inf X (инфимум)-это точная нижняя грань. Поставим вопрос: всякое ли ограниченное множество имеет точные грани?
Пример: Х = {x: x>0} не имеет наименьшего числа.
Теорема о сущ-нии точной верх (ниж) грани. Всякое непустое огранич сверху (снизу) мн-во xR имеет точ верх(ниж) грань.
Сходящаяся последовательность — это последовательность элементов множества X, имеющая предел в этом множестве.
Расходящаяся последовательность — это последовательность, не являющаяся сходящейся.
