
- •K 2. Теорема Кронекера — Капелли
- •5. Кривая второго порядка
- •6. Поверхность второго порядка
- •Типы поверхностей второго порядка Цилиндрические поверхности
- •Поверхности вращения
- •Гиперболический параболоид («седло»).
- •Центральные поверхности
- •Предел функции по Гейне
- •Предел функции по Коши
- •Бесконечно малая величина
- •Бесконечно большая величина
- •Свойства бесконечно малых
- •Теорема
- •14. Предельный переход в неравенствах
- •16. Первый замечательный предел:
- •17. Второй замечательный предел
- •18. Непрерывность функции в интервале и на отрезке
- •19. Точки разрыва функции и их классификация
- •22. Понятие производной ф-ции. Непрерывность ф-ции, имеющей производную.
- •23. Понятие дифференцируемости функции.
- •24. Производная обратной функции.
- •25. Производная сложной функции.
- •26. Производная параметрически заданной функции.
- •27. Производная произведения двух функций.
- •28. Производная частного двух функций.
- •29. Теорема Роля.
- •30. Теорема Ла-Гранжа.
- •31. Теорема Коши.
- •32. Правило Лопиталя.
- •33. Экстремумы функций одной переменной (точки мах и мин).
- •34. Необходимое и достаточное условие монотонности функции.
- •35. Необходимое, достаточное условие экстремума
- •2. Достаточное условие экстремума.
- •36. Выпуклость, вогнутость функции. Точки экстремума.
- •37. Асимптоты.
- •38. Общая схема исследования функции одной переменной.
- •39. Частные производные и диффер. Функции нескольких переменных.
- •40. Производная от сложной функции нескольких переменных.
- •41. Производная неявно заданной функции.
- •42.Производная по направлению. Градиент.
- •43.Касательная плоскость. Нормаль к поверхности.
- •44. Необходимые, достаточные условия существования экстремума функции нескольких переменных.
Предел функции по Гейне
Значение
![]() называется пределом
(предельным
значением)
функции
в
точке
,
если для любой последовательности точек
называется пределом
(предельным
значением)
функции
в
точке
,
если для любой последовательности точек
![]() ,
сходящейся к
,
но не содержащей
в
качестве одного из своих элементов (то
есть в проколотой окрестности
),
последовательность значений функции
,
сходящейся к
,
но не содержащей
в
качестве одного из своих элементов (то
есть в проколотой окрестности
),
последовательность значений функции
![]() сходится
к
.
сходится
к
.
![]()
Предел функции по Коши
Значение
называется
пределом
(предельным
значением)
функции
в
точке
,
если для любого наперёд взятого
положительного числа ε
найдётся отвечающее ему положительное
число
![]() такое,
что для всех аргументов
такое,
что для всех аргументов
![]() ,
удовлетворяющих условию
,
удовлетворяющих условию
![]() ,
выполняется неравенство
,
выполняется неравенство
![]() .
.
![]()
Теорема (единственность предела) Если функция f в точке а имеет предел, то этот предел единственный.
Доказательство: метод от противного limx→af(x)=b,limx→af(x)=c,b/=c . Возьмем ε=∣b−c∣ , по определению и свойству окрестности найдется выколотая окрестность т. а Uo(a,δ), в которой одновременно будут выполняться неравенства ∣f(x)−b∣<2∣b−c∣∣f(x)−c∣<2∣b−c∣ , тогда в точках этой же окрестности ∣b−c∣=∣(b−f(x))+(f(x)+c)∣≤∣f(x)−b∣+∣f(x)−c∣<2∣b−c∣+2∣b−c∣=∣b−c∣ противоречие (от
9. Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю. Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака.
Бесконечно малая величина
Последовательность
an
называется бесконечно
малой, если
![]() .
Например, последовательность чисел
.
Например, последовательность чисел
![]() —
бесконечно малая.
—
бесконечно малая.
Функция называется
бесконечно
малой в окрестности точки
x0,
если
![]() .
.
Функция называется
бесконечно
малой на бесконечности,
если
![]() либо
либо
![]() .
.
Также бесконечно
малой является функция, представляющая
собой разность функции и её предела, то
есть если
![]() ,
то f(x)
− a
= α(x),
,
то f(x)
− a
= α(x),
![]() .
.
Бесконечно большая величина
Во всех приведённых
ниже формулах бесконечность справа от
равенства подразумевается определённого
знака (либо «плюс», либо «минус»). То
есть, например, функция xsin x,
неограниченная с обеих сторон, не
является бесконечно большой при
![]() .
.
Последовательность
an
называется бесконечно
большой,
если
![]() .
.
Функция называется
бесконечно
большой в окрестности точки
x0,
если
![]() .
.
Функция называется
бесконечно
большой на бесконечности,
если
![]() либо
либо
![]() .
.
Свойства бесконечно малых
Сумма конечного числа бесконечно малых — бесконечно малая.
Произведение бесконечно малых — бесконечно малая.
Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.
Если an — бесконечно малая последовательность, сохраняющая знак, то
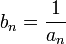 — бесконечно
большая последовательность.
— бесконечно
большая последовательность.
Допустим, у нас
есть бесконечно малые при одном и том
же
![]() величины
α(x)
и β(x)
(либо, что не важно для определения,
бесконечно малые последовательности).
величины
α(x)
и β(x)
(либо, что не важно для определения,
бесконечно малые последовательности).
Если
 ,
то β —
бесконечно малая высшего
порядка малости,
чем α.
Обозначают β
= o(α).
,
то β —
бесконечно малая высшего
порядка малости,
чем α.
Обозначают β
= o(α).Если
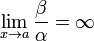 ,
то β —
бесконечно малая низшего
порядка малости,
чем α.
Соответственно α
= o(β).
,
то β —
бесконечно малая низшего
порядка малости,
чем α.
Соответственно α
= o(β).Если
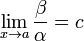 (предел
конечен и не равен 0), то α
и β
являются бесконечно малыми величинами
одного
порядка малости.
(предел
конечен и не равен 0), то α
и β
являются бесконечно малыми величинами
одного
порядка малости.
Это обозначается как β = O(α) или α = O(β) (в силу симметричности данного отношения).
Если
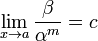 (предел
конечен и не равен 0), то бесконечно
малая величина β
имеет m-й
порядок малости
относительно бесконечно малой α.
(предел
конечен и не равен 0), то бесконечно
малая величина β
имеет m-й
порядок малости
относительно бесконечно малой α.
Для вычисления подобных пределов удобно использовать правило Лопиталя.
Если
![]() ,
то бесконечно малые величины α
и β
называются эквивалентными
(
,
то бесконечно малые величины α
и β
называются эквивалентными
(![]() ).
).
Очевидно, что эквивалентные величины являются частным случаем бесконечно малых величин одного порядка малости.
При
![]() справедливы
следующие соотношения эквивалентности
(как следствия из так называемых
замечательных пределов):
справедливы
следующие соотношения эквивалентности
(как следствия из так называемых
замечательных пределов):
![]()
![]()
![]()
![]()
![]() ,
где a
> 0;
,
где a
> 0;
![]()
![]() ,
где a
> 0;
,
где a
> 0;
![]()
![]()
![]() ,
поэтому используют выражение:
,
поэтому используют выражение:
![]() ,
где
.
,
где
.
