§5. Классическая теория электропроводности в магнитном поле
Электронные свойства материалов, рассмотренные выше, существенно меняются, если кристалл поместить в постоянное магнитное поле. Эти изменения вызываются силой Лоренца, действующей на электроны проводимости
,
(7.5.1)
где E
– напряжённость электрического поля,
B – магнитная
индукция. В отсутствие электрического
поля электрон под действием магнитного
поля совершает ларморову прецессию с
циклотронной частотой
вокруг направления B.
Так как движение происходит в плоскости,
перпендикулярной полю, то энергия
электрона не меняется, оно является
периодическим и квантовано в единицах
.
В пределе больших квантовых чисел это
квантование становится несущественным,
и хорошее описание ряда электромагнитных
явлений даёт уравнение Больцмана.
Воспользовавшись приближением времени
релаксации и записав столкновительный
член, в форме
(изменение импульса за время релаксации)
получим уравнение Больцмана для движения
электрона в классическом приближении
(7.5.2)
Приняв для магнитного поля вектор B = (0,0,B). В декартовых координатах получим три уравнения
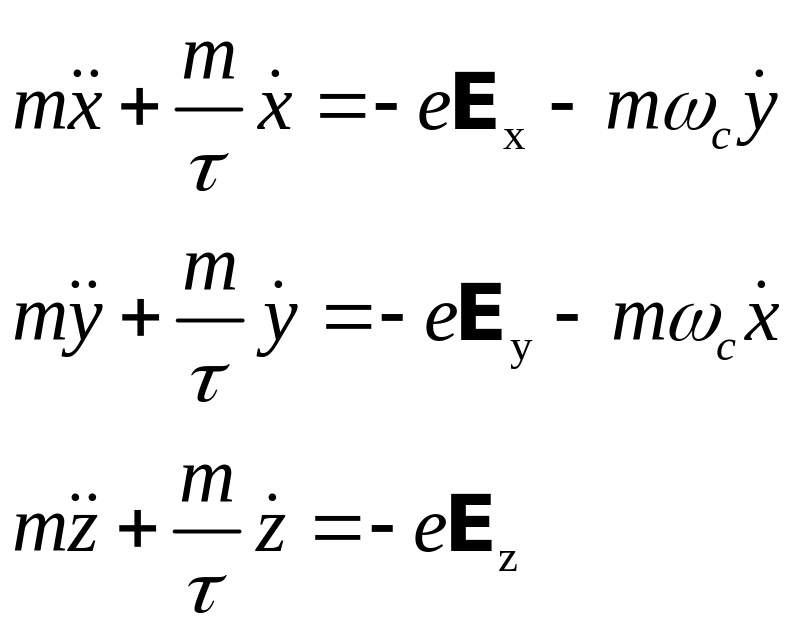(7.5.3)
Положим
,
то вычисление z –
компоненты плотности электрического
тока можно сделать точно так же, как и
в предыдущем параграфе. Из последнего
уравнения (6.5.3) получаем
,
(7.5.4)
откуда следует, что
.
Таким образом, компонента
тензора проводимости
есть
,
(7.5.5)
где
– статическая проводимость в нулевом
магнитном поле.
Проводимость в плоскости
(xy) может быть вычислена
аналогичным образом. Введём комплексную
переменную
,
тогда первые два уравнения (6.5.3) могут
быть сведены к одному уравнению
,
где
.
Следовательно
,
Так что для плотности тока в плоскости (xy) получаем
,
где
,
а компоненты тензора проводимости в
плоскости (xy), даются
выражением
.
(7.5.6)
Этот результат
показывает, что проводимость и ряд
других констант, например, коэффициенты
отражения и поверхностного поглощения
и т.д., связанных с проводимостью
обнаруживают резонансную линию шириной
на частоте
.
Это явление называют циклотронным
резонансом.
Теперь используя связь
И уравнение (7.3.5) легко получить компактной форме закон Ома
.
(7.5.7)
Глава VIII Растворы и химические соединения Введение
Подавляющее большинство химических элементов используется в промышленности не в чистом виде, а в сочетании с другими элементами, добавляемыми для улучшения тех или иных свойств материала. Например, сталь представляет собой в основном сплав железа с углеродом, хотя в её состав обычно входят и многие другие элементы - марганец, никель, хром, и т.д. Для повышения прочности к алюминию добавляют такие металлы как медь, кремний и магний. Из сплавов кремния с малыми добавками мышьяка или индия, можно изготовить твёрдые выпрямители тока.
Свойство
материала, полученного при двух или
более элементов, зависят от нескольких
переменных величин – температуры,
давления, а также от относительной
концентрации исходных элементов. Для
характеристики конечного продукта,
образующегося при таком комбинировании
элементов, используется понятие фазы.
Фаза определяется как часть системы,
имеющая ограничивающую её поверхность,
а также обладающая специфическим
расположением атомов и одинаковыми
интенсивными свойствами (например,
температурой, давлением и т. д.). Ясно,
что несколько таких частей с одинаковыми
интенсивными свойствами представляют
одну и ту же фазу. Лёд, например,
представляет одну фазу
,
а жидкая вода – другую. Смесь этих двух
фаз при одинаковой температуре является
двух фазной системой. Вода, в которой
растворён воздух – это одна фаза, потому,
что для разделения воды и воздуха
необходимо изменение интенсивных
параметров (температуры или давления).
Фазовая диаграмма – это графический
способ описания фаз, находящихся в
равновесии, при различных сочетаниях
переменных величин (состава, давления
и температуры).
Комбинация различных химических элементов при определённой температуре, называют раствором. Твёрдые растворы образуются в том случае, когда атомы различных элементов, смешиваясь в разных соотношениях, способны образовать общую кристаллическую решётку. В настоящее время твёрдо установлено, что все металлы и соединения обнаруживают некоторую растворимость в твёрдом состоянии, причём большой интерес представляет вопрос о величине растворимости в каждом конкретном случае. Например, в – железе может раствориться лишь 0.2 весовых процентов фосфора, тогда как в меди можно растворить около 39 вес. % цинка без изменения структуры. При сплавлении меди с никелем кубическая гранецентрированная решётка сохраняется во всём интервале концентраций, в связи, с чем данная система может служить примером неограниченной взаимной растворимости компонентов в твёрдом состоянии. Если область твёрдого раствора на диграмме состочния не выходит за пределы той части диаграммы, которая примыкает к чистым компонентам,то такие твёрдые растворы называются ограниченными. Разумеется, эти растворы имеют ту же структуру, что и компоненты, на основе которых они образуются. Все остальные фазы, образующиеся в системе, обычно называются промежутоными фазами; их можно назвать интерметаллическими соединениями или валентными соединениями, если растворимость в твёрдом состоянии ограничивается чрезвычайно малой областью вблизи стехиометрического состава. Структура промежуточных фаз зачастую отличается от структуры обоих компонетов, из которых они образуются.
Наука о способах комбинирования различных элементов для получения сплавов с нужными свойствами представляет важнейшую составную часть в общем комплексе инженерных дисциплин. Большинство промышленных сплавов создавалось эмпирически - методом проб и ошибок, и для этого требовалось очень много времени. Разработка сплава является, как правило, очень трудоёмким процессом. Поэтому постоянно ведутся поиски методов, которые позволили бы сократить период создания нужного сплава. В результате напряжённых исследований накоплена обширная информация о различных сочетаниях элементов. Чтобы представит в сжатой форме определённые аспекты этой информации, инженеры и научные работники пользуются главным образом методом фазовых диаграмм.