
- •Физика конденсированного состояния вещества
- •Вводная глава
- •§1. Понятие пространства и времени.
- •§2.Масса, энергия, относительность
- •§3.Симметрия и асимметрия в неживой природе.
- •Глава I. Абстрактные группы
- •§1.Группа
- •§2.Сдвиг по группе
- •§3.Подгруппа
- •§4.Сопряжённые элементы и класс
- •§5.Инвариантная подгруппа
- •§6.Фактор – группа
- •§7. Изоморфизм и гомоморфизм групп
- •§8. Представления групп
- •§9. Характеры представлений
- •§10.Регулярное представление
- •§11. Примеры групп имеющих, приложение в физике
- •§12.Теория групп и квантовая механика
- •Глава II.Описание структуры кристаллов
- •§1.Общие свойства макроскопических тел
- •§2. Точечные группы.
- •§3. Симметрия кристаллов
- •§4.Сингонии.
- •§5.Неприводимые представления группы трансляций
- •§5.Конкретные примеры прямой и обратной решёток
- •1) Прямые решётки.
- •§6.Обозначения узлов, направлений и плоскостей в кристалле
- •§7.Определение структуры кристаллов.
- •§8. Атомный и геометрический структурный факторы
- •Глава III Движение электрона в периодическом поле
- •§1. Адиабатическое приближение
- •§2. Уравнения Хартри
- •§3 Уравнения Хартри-Фока
- •§4.Обменное взаимодействие
- •§5. Кристаллический потенциал и свойства симметрии гамильтониана
- •§6. Теорема Блоха
- •§7. Одноэлектронное уравнение Шрёдингера
- •§8. Приближение свободных электронов
- •§9. Плотность состояний
- •§10. Эффективная масса электронов
- •§11.Приближение почти свободных электронов
- •§12.Метод сильной связи
- •§13. Поверхность Ферми
- •§14. Химический потенциал и физическая статистика
- •Глава IV. Силы связи в кристаллах
- •§1. Силы Ван - дер – Ваальса
- •§2. Ионные кристаллы
- •§3.Ковалентная связь
- •§4. Металлическая связь
- •§5.Водородная связь.
- •Глава V. Динамика решётки.
- •§1. Силы упругости в кристаллах.
- •§2.Колебания и волны в одномерной атомной цепочке.
- •§3. Колебания и волны в двухатомной одномерной цепочке
- •§ 4.Нормальные колебания в трёхмерных кристаллах
- •§5. Понятие о фононах
- •§6.Спектр нормальных колебаний решётки.
- •§7.Теплоёмкость твёрдого тела
- •§8.Теплоёмкость электронного газа
- •Глава VI. Физика полупроводников
- •§1.Собственные полупроводники
- •§2. Примесные полупроводники
- •§3.Статистика электронов и дырок в полупроводниках
- •§4.Положение уровня Ферми и концентрация носителей в собственных полупроводниках
- •§5. Положение уровня Ферми и концентрация носителей в примесных полупроводниках.
- •Глава VII Кинетические свойства твёрдых тел
- •§1. Электропроводность
- •§2. Вычисление времени релаксации
- •§3. Кинетическое уравнение Больцмана
- •§4.Статическая проводимость
- •§5. Классическая теория электропроводности в магнитном поле
- •Глава VIII Растворы и химические соединения Введение
- •§1. Фазовая диаграмма.
- •§2. Упорядоченные растворы.
- •§3.Фазовые превращения.
- •§4. Типы фазовых диаграмм.
- •§5. Системы с образованием химических соединений
- •§6. Сплавы типа растворов внедрения.
- •§7. Упорядочение в сплавах
- •§8. Электронное строение сплавов и неупорядоченных систем
- •§9. Ближний порядок в сплавах
- •§10. Статистическая теория ближнего порядка
- •§11. Факторы, обусловливающие ближний порядок
- •Глава IX.Строение жидкостей и аморфных тел
- •§1. Особенности твёрдого, жидкого и газообразного состояний вещества
- •§2. Радиальные функции распределения межатомных расстояний и атомной плотности
- •§3. Функции распределения в статистической физике
- •§4.Уравнение для бинарной функции распределения
- •§5. Решение уравнения для бинарной функции распределения
- •§6.Уравнение Перкуса – Йевика
- •Глава X.Элементы физики жидких кристаллов Введение
- •§1.Классификация жидких кристаллов
- •2.Смектики c.
- •Смектики b.
- •Заключение. Фуллерены. Углеродные нити
§3. Кинетическое уравнение Больцмана
Как ясно из проведённого в предыдущих параграфах анализа, для описания проводимости в твёрдых телах необходимо использовать квантовую механику. Но ввиду того, что явления переноса связано с реакцией электронов в определённых энергетических зонах на внешнее электрическое и (или) магнитное поля и градиенты температур, и регулируется столкновениями с примесями и другими нарушениями периодичности решётки, о полном квантовомеханическом описании такого явления не может быть и речи. Для этой цели оказывается справедливым, кинетическое уравнение Больцмана. При построении этого уравнения фундаментальное значение имеет запись «интеграла столкновений» – члена, описывающего сравнительно редкие столкновения электронов.
Чтобы получить выражение для интеграла столкновений необходимо найти полное решение задачи о рассеянии электронов. Это решение требует знания законов их взаимодействия с колебаниями решётки, с примесями и т. д. Однако развитие электронной теории металлов показало, что имеется большое число неравновесных кинетических свойств металлов, слабо зависящих от детальной структуры интеграла столкновений и определяемых, главным образом, законом дисперсии электронов проводимости. Это даёт возможность основное внимание уделить полевой (силовой) части кинетического уравнения, почти не занимаясь исследованием структуры интеграла столкновений.
Первым шагом
в квазиклассической теории переноса
является введение величины
![]() ,
характеризующей распределение носителей
с определённым волновым вектором k
в окрестности точки r
в данный момент времени t,т.
е. в элементе фазового объёма
,
характеризующей распределение носителей
с определённым волновым вектором k
в окрестности точки r
в данный момент времени t,т.
е. в элементе фазового объёма
![]() .
Тогда функциональное выражение n
drdk
даёт число носителей в момент времени
t в элементе объёма
фазового пространства. Далее, так как
n изменяется со
временем. Мы опишем это изменение,
подсчитывая число частиц, которые
приходят и покидают элемент фазового
объёма, причём полное число частиц N
определяется выражением
.
Тогда функциональное выражение n
drdk
даёт число носителей в момент времени
t в элементе объёма
фазового пространства. Далее, так как
n изменяется со
временем. Мы опишем это изменение,
подсчитывая число частиц, которые
приходят и покидают элемент фазового
объёма, причём полное число частиц N
определяется выражением
![]() .
(7.3.1)
.
(7.3.1)
Пусть носитель совершает случайные блуждания и не рассеивается вовсе. Тогда будет справедливо следующее соотношение
![]() ,
,
или же
![]() .
.
Отсюда можно получить, что
![]() ,
(7.3.2)
,
(7.3.2)
где
![]() и
и
![]() – операторы градиента по координатам
и волновому вектору соответственно.
Введём скорость v и
силу F, действующую
на носители, следующим образом
– операторы градиента по координатам
и волновому вектору соответственно.
Введём скорость v и
силу F, действующую
на носители, следующим образом
![]() .
(7.3.3)
.
(7.3.3)
Тогда вместо (6.3.2) получим
![]() .
(7.3.4)
.
(7.3.4)
Это и есть так называемое бесстолкновительное уравнение Больцмана. Оно описывает движение носителей в фазовом пространстве.
Введём столкновения
В реальных кристаллах носители сталкиваются между собой. Ограничимся рассмотрением столкновений, идущих с сохранением энергии. В этом случае можно получить обобщённое уравнение Больцмана, учтя эти процессы введением столкновительного члена.
![]() .
(7.3.5)
.
(7.3.5)
Даже
исследование процессов упругих
столкновений является очень сложной
задачей. Введём микроскопическую
вероятность рассеяния
![]() электрона в единицу времени из занятого
состояния с волновым вектором k,
в незаполненное состояние с волновым
вектором
.
Тогда используя статистику Ферми,
получим
электрона в единицу времени из занятого
состояния с волновым вектором k,
в незаполненное состояние с волновым
вектором
.
Тогда используя статистику Ферми,
получим
![]() ,
(7.3.6)
,
(7.3.6)
где
![]() .
В выражении (6.3.6) I(n)
– интеграл столкновений – сложный
функционал от функций распределения,
структура и конкретный вид которого
определяется взаимодействием электронов
с примесями, друг с другом и другими
квазичастицами. В последнем случае
(6.3.6) должна быть дополнена функциями
распределения других квазичастиц.
Отметим здесь ещё, что интеграл
столкновений обращается в нуль равновесной
функцией распределения Ферми
.
В выражении (6.3.6) I(n)
– интеграл столкновений – сложный
функционал от функций распределения,
структура и конкретный вид которого
определяется взаимодействием электронов
с примесями, друг с другом и другими
квазичастицами. В последнем случае
(6.3.6) должна быть дополнена функциями
распределения других квазичастиц.
Отметим здесь ещё, что интеграл
столкновений обращается в нуль равновесной
функцией распределения Ферми
![]() с произвольными значениями параметров
температуры и химического потенциала.
Когда тепловое равновесие устанавливается,
одни столкновения не изменяют полной
плотности точек в фазовом пространстве,
и тогда интеграл столкновений обращается
в нуль. Откуда следует так называемый
принцип детального равновесия
с произвольными значениями параметров
температуры и химического потенциала.
Когда тепловое равновесие устанавливается,
одни столкновения не изменяют полной
плотности точек в фазовом пространстве,
и тогда интеграл столкновений обращается
в нуль. Откуда следует так называемый
принцип детального равновесия
![]() .
(7.3.7)
.
(7.3.7)
Линеаризация уравнения Больцмана
Для ряда задач, связанных с переносом, допустимо предположение, что установившееся в поле стационарное распределение n при изотермических условиях не очень отличается от равновесного распределения. Тогда задача сводится к нахождению распределения возбуждённых состояний
![]() .(7.3.8)
.(7.3.8)
Это даёт
возможность сильно упростить задачу,
в особенности, когда мы интересуемся
только линейными членами порядка
![]() в линейном по полю F,уравнении
Больцмана. Так, например, легко решается
задача нахождения постоянного тока в
однородном электрическом поле.
Линеаризацией можно свести уравнение
(7.3.5) к виду
в линейном по полю F,уравнении
Больцмана. Так, например, легко решается
задача нахождения постоянного тока в
однородном электрическом поле.
Линеаризацией можно свести уравнение
(7.3.5) к виду
![]() ,
(7.3.9)
,
(7.3.9)
где
![]() .
.
Выражение (6.4.9) называется линеаризованным уравнением Больцмана.
Приближение времени релаксации
Пусть отклонение
от равновесного распределения
![]() вызвано внешним полем, которое выключается
в момент времени t=0.
Тогда
спадает экспоненциально за характерное
время
– время релаксации
вызвано внешним полем, которое выключается
в момент времени t=0.
Тогда
спадает экспоненциально за характерное
время
– время релаксации
![]() .
(7.3.10)
.
(7.3.10)
Это означает, что в изотермических условиях (когда отсутствует диффузный член) и в нулевом поле уравнение (6.3.9) сводится к виду
![]() .(7.3.11)
.(7.3.11)
Соответственно, если поддерживать постоянным поле F, устанавливается стационарное состояние, в котором
![]() ,
(7.3.12)
,
(7.3.12)
где
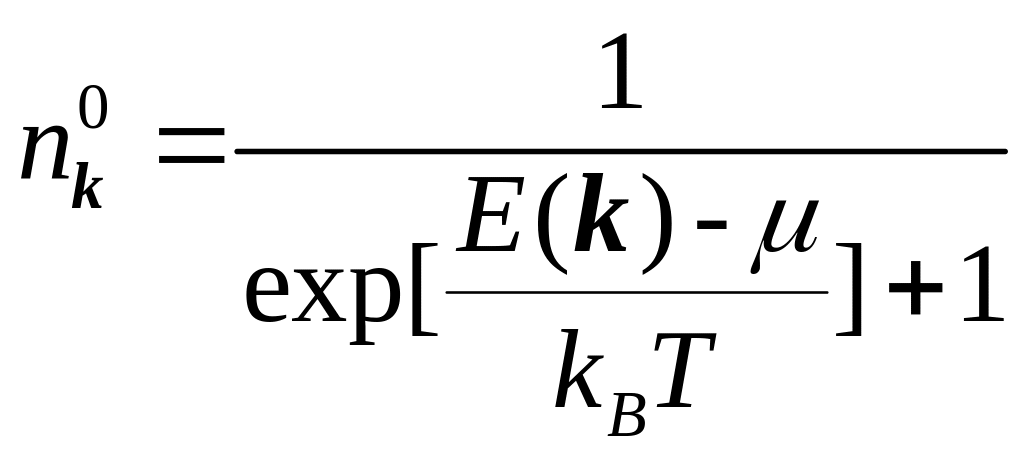 ,
,
– химический потенциал.
