§2. Вычисление времени релаксации
Проводить вычисления проводимости квантовомеханическим путём является очень сложной задачей. Поэтому мы проведём здесь лишь некоторые общие физические соображения, основанные на применении ньютоновской механики к движению заряженных частиц и на концепции распределения Ферми – Дирака.
Начнём с констатации того факта, что в отсутствие электрического поля никакого тока в веществе быть не может. Это утверждение следует из свойств распределения Ферми, поскольку для каждого электрона с импульсом в каком – то направлении в кристалле найдётся другой электрон, имеющий импульс противоположного направления. Однако эта компенсация импульсов тотчас нарушается, если на кристалл наложить внешнее электрическое поле. При наличии поля каждый электрон будет испытывать действие силы в одном и том же направлении, и все электроны, находящиеся внутри сферы Ферми, получат ускорение в направлении противоположном направлению электрического поля (см. рис.).
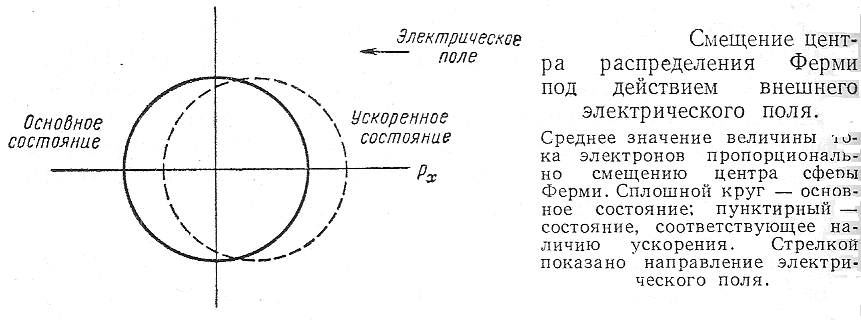
При смещении сферы Ферми электронов в k – пространстве образуется определённое число дырок. Это может произойти, только, если первая зона Бриллюэна не полностью заполнена, и объясняет, почему металлы являются хорошими проводниками, в то время как диэлектрики полупроводники не проводят ток при нулевой температуре.
Тормозящие силы, связанные с рассеянием отдельных электронов решёткой, особенно сильно проявляются для внешней части распределения Ферми. Электроны, находящиеся в передней, «носовой» части сферы Ферми (в положительном направлении оси x), рассеиваются чаще, чем те, которые находятся «сзади». Поэтому электроны покидают переднюю, часть сферы и постепенно переходят в состояния с меньшей энергией, расположенные в противоположной части сферы. Когда процессы рассеяния станут компенсировать эффекты ускорения под действием поля, установится стационарное состояние, и сфера Ферми будет оставаться в одном и том же смещённом положении.
Вычислять
величину смещения центра сферы, следовало
бы, опираясь полностью на квантовую
механику. Однако это представляет
сложную задачу. Поэтому здесь мы приведём
некоторые общие физические соображения,
и получим те результаты, которые сохраняют
силу и при квантовом рассмотрении.
Смещение поверхности Ферми происходит
следующим образом. Так как для свободных
электронов скорость
,
уравнение движения электронов, находящихся
на поверхности Ферми, под действием
постоянного электрического поля имеет
вид
,
Откуда следует, что в отсутствие столкновений сфера Ферми будет смещаться в k – пространстве с постоянной скоростью. Интегрируя уравнения движения, получим
.
Таким образом, при
наличии электрического поля центр
заполненной сферы Ферми за некоторое
характерное время
сместится на величину
.
Столкновения препятствуют этому эффекту, стремясь вернуть сферу в исходное положение, откуда снова получаем классическую формулу для проводимости (6.1.6).
В предыдущем параграфе с классической точки зрения мы уже получили выражение (6.1.6) для электропроводности. Теперь проведённое рассмотрение рассмотрим на языке квантовой механики, пользуясь представлением энергетических зон. Введённая в первом параграфе величина, названная временем релаксации, равна половине интервала времени между двумя последовательными столкновениями. Вспоминая, что в распределении Ферми в столкновениях могут участвовать лишь те электроны, которые обладают энергией близкой к энергии Ферми, то понятие времени между столкновениями следует считать относящимся именно к этим электронам.
Со временем
релаксации связана другая важная
величина, называемая подвижностью
и обозначаемой
(не путать с химическим потенциалом).
Подвижность определяется как средняя
скорость, достигаемая носителем заряда
за время
в поле единичной напряжённости, т.е.
.
Подвижность зависит не только от величины заряда носителя тока, но также и от времени релаксации и эффективной массы. Её можно измерять на опыте, и поэтому она является более полезным понятием, чем время релаксации. Воспользовавшись подвижностью, проводимость можно записать в виде
.
Время релаксации связано также с длиной свободного пробега электронов, способных испытывать соударения. Если скорость, достигаемая электронами в поле, пренебрежимо мала по сравнению со скоростью Ферми, то
,
где
– скорость электронов в верхней части
распределения Ферми. Если в эту формулу
подставить скорость и время релаксации,
соответствующие нормальным металлам,
то получим величину
.
Теперь сделаем несколько замечаний относительно приближений, которые были сделаны в ходе рассмотрения вопроса о проводимости. Все выводы делались в неявном предположении, что и время релаксации и эффективная масса не зависят от направления в кристалле. Эксперименты, однако, показывают, что это не так. Следовательно, проводимость также является функцией направления. Но в случае кубических кристаллов в силу их высокой симметрии векторные соотношения, относящиеся к таким величинам в кристаллах, оказываются не зависящими от направлений, т. е. имеет место изотропия. Тогда время релаксации должно зависеть от направления таким образом, чтобы его отношение к эффективной массе оставалось изотропным. Для кристаллов с более низкой симметрией эта компенсация осуществляется не всегда, и в таких кристаллах (например, гексагональных) проводимость будет являться тензорной величиной.