
- •Физика конденсированного состояния вещества
- •Вводная глава
- •§1. Понятие пространства и времени.
- •§2.Масса, энергия, относительность
- •§3.Симметрия и асимметрия в неживой природе.
- •Глава I. Абстрактные группы
- •§1.Группа
- •§2.Сдвиг по группе
- •§3.Подгруппа
- •§4.Сопряжённые элементы и класс
- •§5.Инвариантная подгруппа
- •§6.Фактор – группа
- •§7. Изоморфизм и гомоморфизм групп
- •§8. Представления групп
- •§9. Характеры представлений
- •§10.Регулярное представление
- •§11. Примеры групп имеющих, приложение в физике
- •§12.Теория групп и квантовая механика
- •Глава II.Описание структуры кристаллов
- •§1.Общие свойства макроскопических тел
- •§2. Точечные группы.
- •§3. Симметрия кристаллов
- •§4.Сингонии.
- •§5.Неприводимые представления группы трансляций
- •§5.Конкретные примеры прямой и обратной решёток
- •1) Прямые решётки.
- •§6.Обозначения узлов, направлений и плоскостей в кристалле
- •§7.Определение структуры кристаллов.
- •§8. Атомный и геометрический структурный факторы
- •Глава III Движение электрона в периодическом поле
- •§1. Адиабатическое приближение
- •§2. Уравнения Хартри
- •§3 Уравнения Хартри-Фока
- •§4.Обменное взаимодействие
- •§5. Кристаллический потенциал и свойства симметрии гамильтониана
- •§6. Теорема Блоха
- •§7. Одноэлектронное уравнение Шрёдингера
- •§8. Приближение свободных электронов
- •§9. Плотность состояний
- •§10. Эффективная масса электронов
- •§11.Приближение почти свободных электронов
- •§12.Метод сильной связи
- •§13. Поверхность Ферми
- •§14. Химический потенциал и физическая статистика
- •Глава IV. Силы связи в кристаллах
- •§1. Силы Ван - дер – Ваальса
- •§2. Ионные кристаллы
- •§3.Ковалентная связь
- •§4. Металлическая связь
- •§5.Водородная связь.
- •Глава V. Динамика решётки.
- •§1. Силы упругости в кристаллах.
- •§2.Колебания и волны в одномерной атомной цепочке.
- •§3. Колебания и волны в двухатомной одномерной цепочке
- •§ 4.Нормальные колебания в трёхмерных кристаллах
- •§5. Понятие о фононах
- •§6.Спектр нормальных колебаний решётки.
- •§7.Теплоёмкость твёрдого тела
- •§8.Теплоёмкость электронного газа
- •Глава VI. Физика полупроводников
- •§1.Собственные полупроводники
- •§2. Примесные полупроводники
- •§3.Статистика электронов и дырок в полупроводниках
- •§4.Положение уровня Ферми и концентрация носителей в собственных полупроводниках
- •§5. Положение уровня Ферми и концентрация носителей в примесных полупроводниках.
- •Глава VII Кинетические свойства твёрдых тел
- •§1. Электропроводность
- •§2. Вычисление времени релаксации
- •§3. Кинетическое уравнение Больцмана
- •§4.Статическая проводимость
- •§5. Классическая теория электропроводности в магнитном поле
- •Глава VIII Растворы и химические соединения Введение
- •§1. Фазовая диаграмма.
- •§2. Упорядоченные растворы.
- •§3.Фазовые превращения.
- •§4. Типы фазовых диаграмм.
- •§5. Системы с образованием химических соединений
- •§6. Сплавы типа растворов внедрения.
- •§7. Упорядочение в сплавах
- •§8. Электронное строение сплавов и неупорядоченных систем
- •§9. Ближний порядок в сплавах
- •§10. Статистическая теория ближнего порядка
- •§11. Факторы, обусловливающие ближний порядок
- •Глава IX.Строение жидкостей и аморфных тел
- •§1. Особенности твёрдого, жидкого и газообразного состояний вещества
- •§2. Радиальные функции распределения межатомных расстояний и атомной плотности
- •§3. Функции распределения в статистической физике
- •§4.Уравнение для бинарной функции распределения
- •§5. Решение уравнения для бинарной функции распределения
- •§6.Уравнение Перкуса – Йевика
- •Глава X.Элементы физики жидких кристаллов Введение
- •§1.Классификация жидких кристаллов
- •2.Смектики c.
- •Смектики b.
- •Заключение. Фуллерены. Углеродные нити
§1. Силы упругости в кристаллах.
В предыдущей главе было показано, что между частицами, составляющими твёрдые тела, существуют как силы притяжения, так и отталкивания. Почти во всех случаях представляется более удобным оперировать не с силами, а спотенциальной энергией взаимодействия атомов U(R), которую мы предполагаем зависящей только отрасстояния R между ядрами атомов. Эта зависимость, в принципе, может иметь вид аналогичной формуле, например, Борна–Майера. Зависимость потенциальной энергии от расстояния R может быть представлена в виде (см. рис.)
К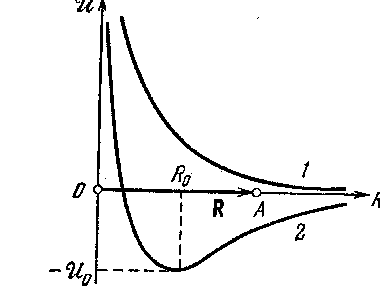 ривые
1 и 2 изображают возможные случаи
взаимодействия атомов, один из которых
помещён в начале координат 0, а другой
атом A может перемещаться
вдоль оси R. Так как
потенциальная энергия определяется с
точностью до произвольной постоянной,
то её можно положить равной нулю. Сила,
действующая на атом A,
равна
ривые
1 и 2 изображают возможные случаи
взаимодействия атомов, один из которых
помещён в начале координат 0, а другой
атом A может перемещаться
вдоль оси R. Так как
потенциальная энергия определяется с
точностью до произвольной постоянной,
то её можно положить равной нулю. Сила,
действующая на атом A,
равна
![]() ,
где
,
где
![]() –
радиус вектор, проведённый от точки 0
к точке А. Легко понять что, в тех точках,
где
–
радиус вектор, проведённый от точки 0
к точке А. Легко понять что, в тех точках,
где![]() ,
имеют место силы притяжения, и наоборот
имеют место силы отталкивания. Из рисунка
видно, что силам отталкивания, отвечает
кривая 1. Кривая 2 сответствует более
сложному случаю, Когда
,
имеют место силы притяжения, и наоборот
имеют место силы отталкивания. Из рисунка
видно, что силам отталкивания, отвечает
кривая 1. Кривая 2 сответствует более
сложному случаю, Когда
![]() атомы притягиваются, а в случае
атомы притягиваются, а в случае
![]() ,
отталкиваются друг от друга. Далее,
,
отталкиваются друг от друга. Далее,
![]() ,
т.е. в этой точке сила равна нулю. Значит,
система из обоих атомов находится в
состоянии устойчивого равновесия. В
этом случае для кривой 2, имеем
,
т.е. в этой точке сила равна нулю. Значит,
система из обоих атомов находится в
состоянии устойчивого равновесия. В
этом случае для кривой 2, имеем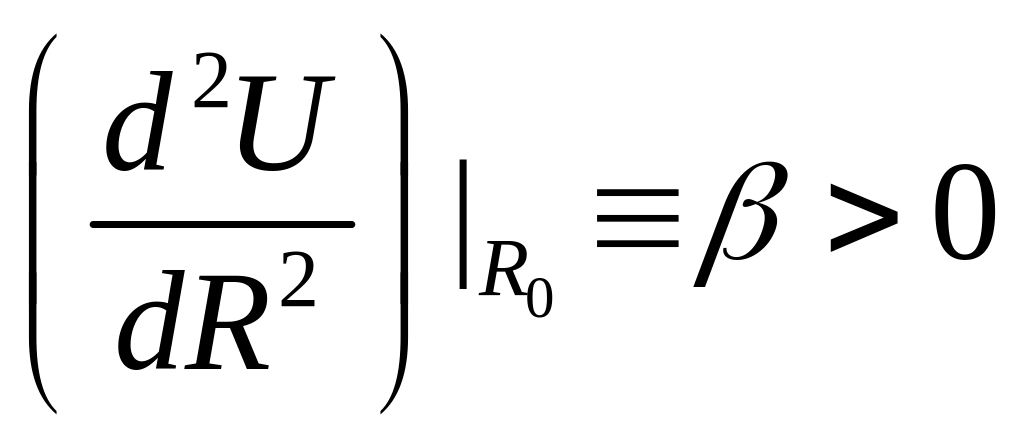 .
При малых отклонениях атомов от положения
равновесия потенциальную энергию
разложим в ряд по этим малым отклонениям
.
При малых отклонениях атомов от положения
равновесия потенциальную энергию
разложим в ряд по этим малым отклонениям
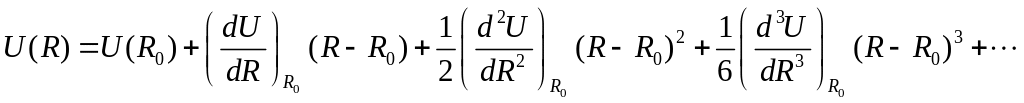 (5.1.1)
(5.1.1)
С точностью до величин
третьего плорядка малости. Вблизи точки
![]() ,
силы отталкивания возрастают быстрее,
чем убывают силы притяжения, поэтому
можно записать такое соотношение
,
силы отталкивания возрастают быстрее,
чем убывают силы притяжения, поэтому
можно записать такое соотношение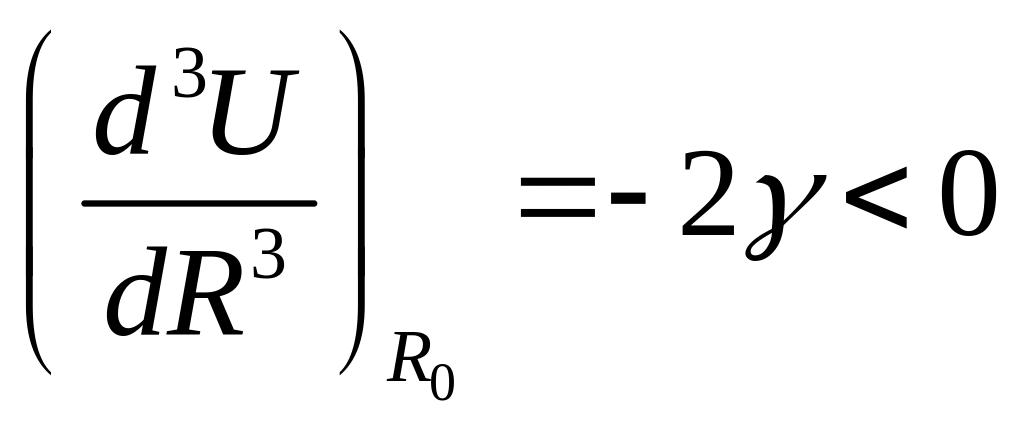 .
Обозначая
.
Обозначая
![]() ,
а отклонение от положения равновесия
обозначим x
,
а отклонение от положения равновесия
обозначим x![]() ,
получим
,
получим
![]() .
(5.1.2)
.
(5.1.2)
Тогда по определению сила, действующая на ато при движении его вблизи положения равновесия вдоль оси R, будет равна
![]() .
(5.1.3)
.
(5.1.3)
Первое слагаемое в правой части этого выражения, как известно, определяет квазиупругую силу. Кристалл, для которого применяется сила в таком приближении, называют гармоническим кристаллом.
§2.Колебания и волны в одномерной атомной цепочке.
Рассмотрим совокупность ионов массой M, вдоль прямой в точках, отстоящих друг от друга на расстоянии a,так что векторы одномерной решётки Бравэ есть просто R=na, где n – целое число. Пусть u(na) – отклонение иона в точке na вдоль прямой, отсчитываемое от его равновесного пложения. Оно описывает смещение иона вблизи точки na см. рис.
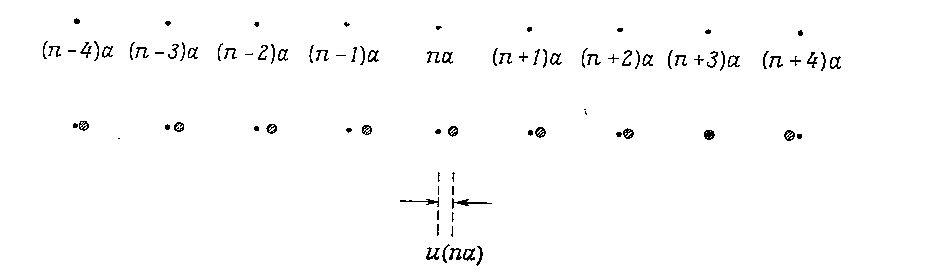
Для простоты предположим,что взаимодействуют лишь соседние ионы; тогда потенциальная энергия будет иметь вид
![]() .
(5.2.1)
.
(5.2.1)
После определения силы как производной от потенциальной энергии можем записать уравнения движения в форме Ньютона
![]() .
(5.2.2)
.
(5.2.2)
Если число
ионов в цепочке, конечно, необходимо
указать, как описывать ионы на двух её
концах. Однако, если число ионов велико
и нас не интересуют эффекты, происходящие
наконцах цепочки мы можем воспользоваться
подходом, который даёт наибольшие
математические преимущества. Как и в
случае электронного газа, удобнее всего
выбрать периодические циклические
условия Борна–Кармана. Для линейной
цепочки это граничное условие допускает
простую формулировку: мы соединяем два
противоположных конца цепочки, тем
самым, отождествляя ион номер 1, с ионом
номер N+1. Таким образом,
для решений получаем следующие условия
![]() .
Будем искать решение уравнений Ньютона
в виде
.
Будем искать решение уравнений Ньютона
в виде
![]() .
Тогда из периодического граничного
условия вытекает требование
.
Тогда из периодического граничного
условия вытекает требование
![]() ,
откуда в свою очередь следует, что
величина q должна
иметь следующий вид
,
откуда в свою очередь следует, что
величина q должна
иметь следующий вид
![]() ,
n – целое число.
(5.2.2а)
,
n – целое число.
(5.2.2а)
Заметим, что
при изменении q на
смещение
![]() ,
не меняется. Следовательно, имеется
лишь N значений q,
согласующихся с требованиями граничных
условий и дающих физически различные
решения. Будем считать, что эти значения
лежат в интервале от значения
,
не меняется. Следовательно, имеется
лишь N значений q,
согласующихся с требованиями граничных
условий и дающих физически различные
решения. Будем считать, что эти значения
лежат в интервале от значения
![]() до
до
![]() .
Так в одномерном случае выглядит
требование, чтобы вектор q
лежал в первой зоне Бриллюэна. После
подстановки предлагаемого решения в
уравнение Ньютона получим
.
Так в одномерном случае выглядит
требование, чтобы вектор q
лежал в первой зоне Бриллюэна. После
подстановки предлагаемого решения в
уравнение Ньютона получим
![]() (5.2.3)
(5.2.3)
Решение этого
уравнения существует, если
![]() ,
где
,
где
![]() .
(5.2.4)
.
(5.2.4)
Решения, описывающие реальные смещения частиц, даются действительной или мнимой частью
![]() или
или
![]() .(5.2.5)
.(5.2.5)
Поскольку
![]() –
чётная функция q,
достаточно взять лишь положительный
корень в (5.2.4): решения (5.2.5), определяемые
значенмями q и
–
чётная функция q,
достаточно взять лишь положительный
корень в (5.2.4): решения (5.2.5), определяемые
значенмями q и
![]() ,
совпадают с решениями, определяемые
значениями – q и
,
совпадают с решениями, определяемые
значениями – q и
![]() .
Таким образом, мы имеем N
различных значений q,
каждое со своей частотой
.
Таким образом, мы имеем N
различных значений q,
каждое со своей частотой
![]() ;
следовательно, формулы (5.2.5) дают 2N
независимых решений. Произвольное
движение цепочки задаётся указанием N
начальных положений и N
начальных скоростей ионов. Поскольку
начальным условиям всегда можно
удовлетворить, выбрав подходящую
комбинацию из 2N
независимых решений, мы нашли полное
решение задачи.
;
следовательно, формулы (5.2.5) дают 2N
независимых решений. Произвольное
движение цепочки задаётся указанием N
начальных положений и N
начальных скоростей ионов. Поскольку
начальным условиям всегда можно
удовлетворить, выбрав подходящую
комбинацию из 2N
независимых решений, мы нашли полное
решение задачи.
Решения
(5.2.5) описывают волны, распространяющиеся
вдоль цепочки с фазовой скоростью
![]() и групповой скоростью
и групповой скоростью
![]() .
Волны u(qa,t)
называются нормальными колебаниями,
а частоты
модами
нормальных колебаний. Частота
как функция волнового вектора q
изображена на рис. Т
.
Волны u(qa,t)
называются нормальными колебаниями,
а частоты
модами
нормальных колебаний. Частота
как функция волнового вектора q
изображена на рис. Т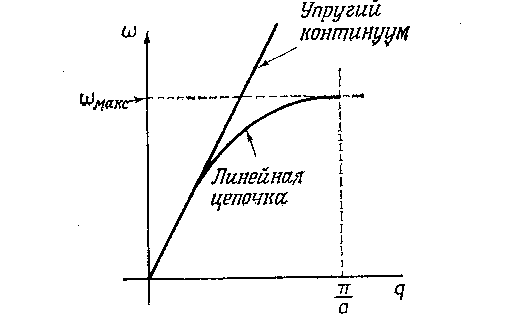 акую
кривую называют дисперсионной. Когда
значение q мало по
сравнению со значением
акую
кривую называют дисперсионной. Когда
значение q мало по
сравнению со значением
![]() (т.е.
когда длина волны велика по сравнению
с расстоянием между частицами), частота
линейно зависит от q
(т.е.
когда длина волны велика по сравнению
с расстоянием между частицами), частота
линейно зависит от q
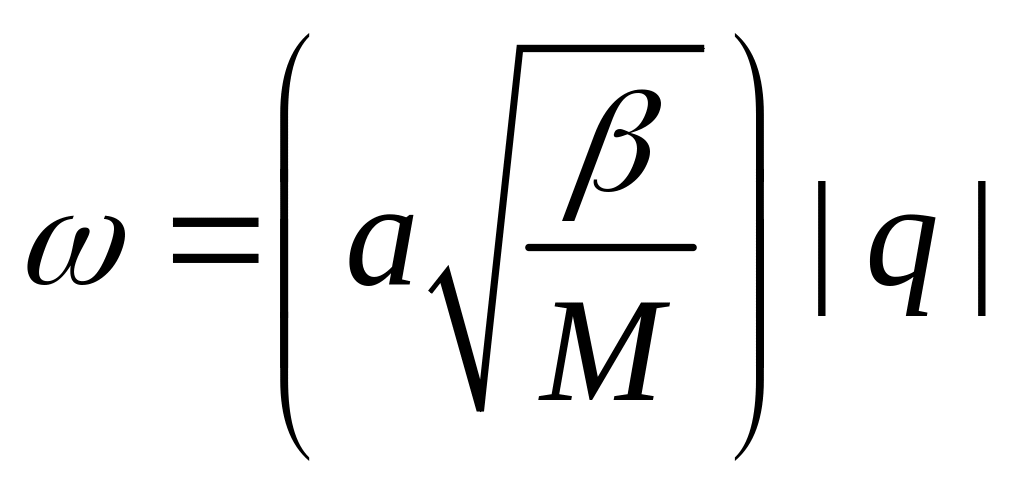 .
(5.2.6)
.
(5.2.6)
Такое поведение
волн, как известно, присуще и световым
и звуковым волнам. На рис. прямой линией
показана дисперсия звуковых волн. Если
частота
линейно зависит от q,
то групповая скорость совпадает сфазовой
и обе они не зависят от частоты. Однако,
в дискретных средах, характерная
особенность волн проявляется в том, что
линейный закон дисперсии перестаёт
соблюдаться при длинах волн, сравнимых
с расстоянием между частицами. В этом
случае
отстаёт от фазовой скорости
![]() с ростом q и в
действительности в точках
с ростом q и в
действительности в точках
![]() дисперсионная кривая становится
горизонтальной, т.е. групповая скорость
спадает до нуля.
дисперсионная кривая становится
горизонтальной, т.е. групповая скорость
спадает до нуля.
