§6.Обозначения узлов, направлений и плоскостей в кристалле

В кристаллографии применяют несколько способов для описания свойств симметрии различных типов кристаллов. Одна из наиболее важных задач состоит в том, чтобы описать направления в кристаллическом пространстве. Так, в некоторых случаях возникает необходимость в определении направления отдельных атомных рядов. Это направление можно определить заданием положения одного из узлов атомного ряда. Положение любого узла решётки относительно выбранного начала координат определяется заданием трёх его координат x,y,z.Эти координаты, в простейшем случае кубической решётки, можно выразить следующим образом:

,

где a- параметр решётки; m,n,p-целые числа.

Если за единицу измерения длин вдоль осей решётки принять параметр решётки, то координатами узла будут просто числа m,n,p.Они называются индексами узла. Для удобства индексы узла заключаются в квадратные скобки [mnp].Отрицательные значения проекций на любую ось имеют отрицательный индекс и отмечаются чертой над соответствующим индексом. Например, для узла с координатами x=2a,y=-1a. z=3a индексы записывают в следующем виде: .

Для описания направления в кристалле выбирается прямая, проходящая через начало координат, Её положение однозначно определяется индексами [mnp] первого узла, через который она проходит, тогда, по определению, индексы направления представляют собой три наименьших целых числа, характеризующих положение ближайшего узла, лежащего в данном направлении. Направления, эквивалентные по характеру симметрии относительно трёх координатных осей, образуют группу. Индексы этих направлений записывают вместе и заключают в угловые скобки: <m n p>. Примеры. Ось +x имеет индексы [100],ось –x – индексы [ ]. Индексы оси + y–[010], - y– [ ]. Диагональ грани xy обозначается индексами [110],а грани xz - [101].Диагональ куба в положительном квадранте имеет индексы [111], а в противоположном направлении [ ]. Восемь диагоналей куба обозначаются как <111>; все они получаются перестановкой индексов .

Индексы плоскости. Атомная плоскость некоторой решётки Бравэ определяется как любая из плоскостей, содержащих, по крайней мере, три не лежащих на одной прямой точки этой решётки. Из-за трансляционной симметрии решётки Бравэ любая такая плоскость в действительности содержит бесконечно много узлов решётки, которые образуют на плоскости двумерную решётку Бравэ. На рисунках для простой кубической решётки представлены возможные выборы плоскостей. Рисунки эти показывают, что выбор плоскостей в кристалле не является однозначным.

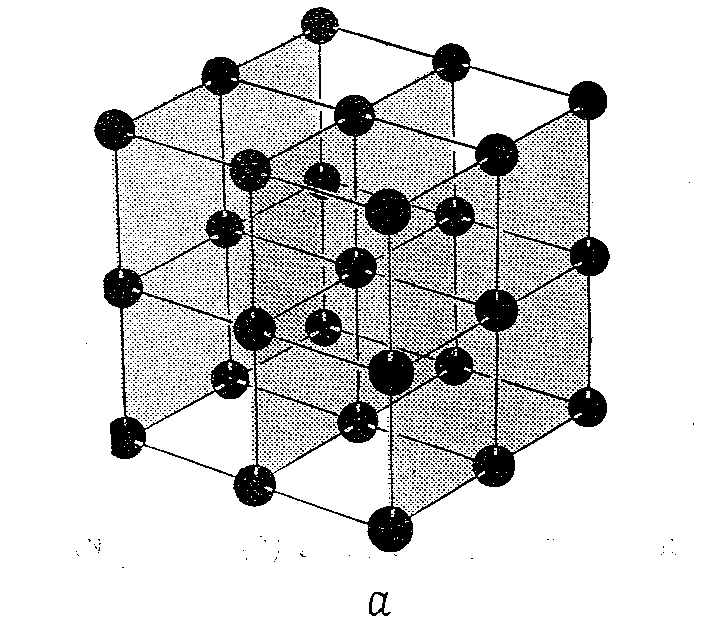
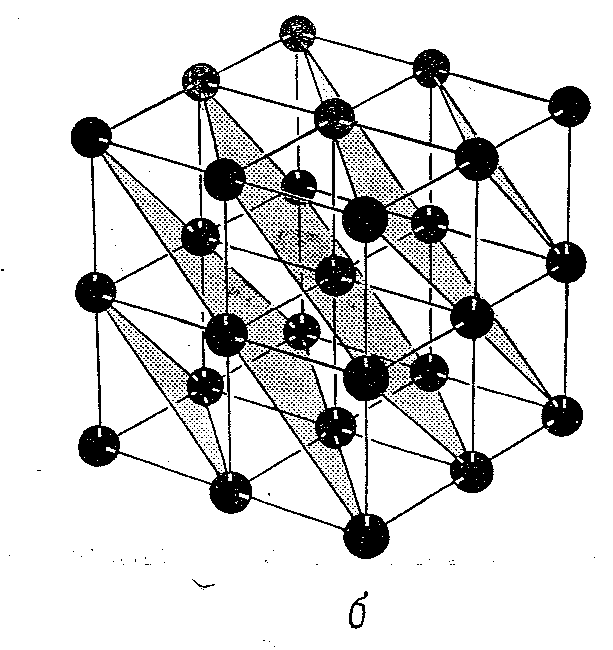
Для выбора конкретной плоскости задают индексы плоскостей. Эти индексы называются индексами Миллера. Положение плоскости определяется заданием трёх отрезков A,B.C, которые она отсекает на осях решётки. Индексы такой плоскости отыскиваются следующим образом.

Выражают отрезки A,B,C в осевых единицах и записывают величины, обратные этим отрезкам: . Полученные дроби приводят к общему знаменателю. Пусть таковым будет число D. Целые числа и являются индексами Миллера. Они записываются в круглых скобках так: (hkl).

Определим, например, индексы плоскости, отсекающей на осях отрезки . Число D, которое приводит обратные значения этих отрезков к целым числам, очевидно, будет равно 2, тогда h=4, k=1, l=6. Плоскость обозначают (416).Плоскость с отрицательным значением индекса x записывается так . У плоскостей кристалла, эквивалентных по характеру симметрии, индексы заключаются в фигурные скобки: {hkl}. Вообще говоря, ориентация плоскости описывается путём задания вектора нормали к этой плоскости. Однако мы знаем, что базисные векторы обратной решётки образуют контравариантный базис. Поскольку векторы этого базиса ортогональны плоскостям (атомным) прямой решётки, то можно говорить, что для всякого семейства атомных плоскостей существуют нормальные к нему векторы обратной решётки, то естественно выбрать в качестве нормали такой вектор обратной решётки. Чтобы сделать этот выбор однозначным, выбирают наименьший из указанных векторов. Таким путём мы определяем индексы Миллера данной плоскости.

Итак, индексы Миллера некоторой атомной плоскости - это координаты наименьшего вектора обратной решётки, перпендикулярного данной плоскости, в системе координат, заданной основными векторами обратной решётки. Следовательно, плоскость, имеющая индексы Миллера h,k,l, перпендикулярна вектору обратной решётки . Отсюда следует так же, что индексы Миллера зависят от выбора основных векторов.

Для кубических решёток с длиной ребра куба равной a расстояние d между соседними плоскостями с индексами (hkl) вычисляется по формуле

Отсюда видно, что расстояния между плоскостями с большими индексами малы по сравнению с расстояниями между плоскостями, имеющими малые индексы. У плоскостей с малыми индексами более высокая плотность расположения атомов, чем у плоскостей с большими индексами.