§4.Сингонии.

Решётки Браве обладают определённой симметрией относительно поворотов и отражений. Для каждой решётки Браве существует точечная группа K преобразований, которые переводят вектор решётки в вектор решётки. Ортогональные преобразования трёхмерного пространства, принадлежащие группе K, будем обозначать через . Существует семь систем (сингоний) кристаллических решёток, различающихся точечной группой К. Оказывается, не всякая точечная группа может быть группой симметрии решётки. Требование, чтобы одновременно с a вектор также был вектором решётки, ограничивает круг допустимых точечных групп. Выясним эти ограничения. Прежде всего, следует отметить, что группа K должна содержать инверсию I: вместе с трансляцией на вектор a в группу всегда входит трансляция на вектор –a. Теперь установим, какие оси симметрии может иметь группа K? Выберем в качестве ортов базиса пространства векторов основные векторы решётки и запишем преобразование в новом базисе, в котором все векторы решётки имеют целочисленные составляющие. Если матрицу ортогональных преобразований обозначить через , то мы будем иметь

,

где - матрица перехода от первоначального ортонормированного базиса к базису . Если - поворот (или зеркальный поворот) на угол , то след матрицы , так же как и след матрицы , равен

.

Однако из условия, что преобразование должно переводить целочисленный вектор решётки в целочисленный вектор, следует, что все элементы матрицы , а, следовательно, и её след должны быть целочисленными. Отсюда получаем, что может принимать лишь следующие значения

.

Следовательно, группа K может содержать оси только второго, третьего, четвёртого и шестого порядков. Есть здесь ещё одно ограничение, которое доказыватьне будем. А сразу сформулируем вывод: все ограничения приводят ктому, что роль точечной группы кристалла могут играть лишь семь точечных групп, а именно:

.

Это и является причиной того, что существует только семь сингоний (систем): триклинная, моноклинная, ромбическая, ромбоэдрическая, тетрагональная, гексагональная, кубическая. Перечислим свойства этих точечных групп:

они содержат инверсию;

не содержат осей 5-го, 7-го и более высоких порядков;

вместе с осью 3-го,4-го или 6-го порядков они содержат также и плоскости, проходящие через эти оси.

Рассмотрим теперь векторные группы, принадлежащие одной и той же сингонии.

Точечная группа решётки Бравэ накладывает определённые ограничения на возможное расположение и относительные длины основных векторов решётки.

Д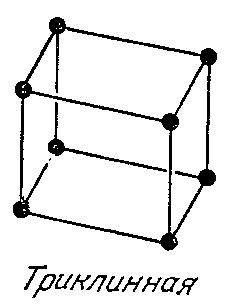 ве векторные группы, принадлежащие одной и той же сингонии, называются однотипными, если одна из них может быть переведена в другую с помощью непрерывной деформации; при этом в процессе деформации симметрия векторной группы должна быть не ниже, чем симметрия групп данной сингонии. Эти требования, предъявляемые к векторным группам, приводят к тому, что существует только 14 типов векторных групп. Рассмотрим подразделение решёток Браве на системы:

1)В триклинной системе единственная пространственная решётка имеет примитивную (Р) элементарную ячейку, в которой все три базисных вектора имеют разную длину, а все углы не равны между собой.

2) В моноклинной системе имеются две пространственные решётки: одна имеет примитивную (Р) элементарную ячейку, другая (С) имеет элементарную ячейку с центрированными основаниями (в центре оснований располагаются узлы) ячейки, нормальных к вектору

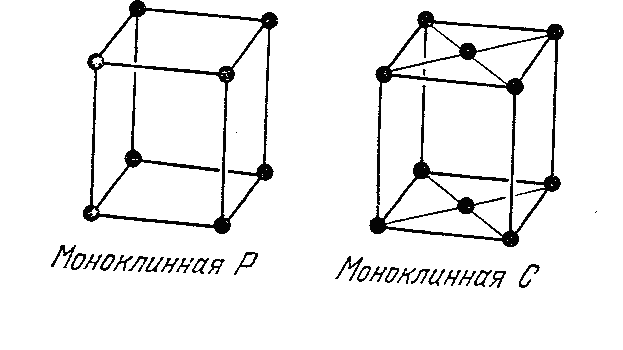
3) В ромбической системе имеется четыре пространственные решётки:

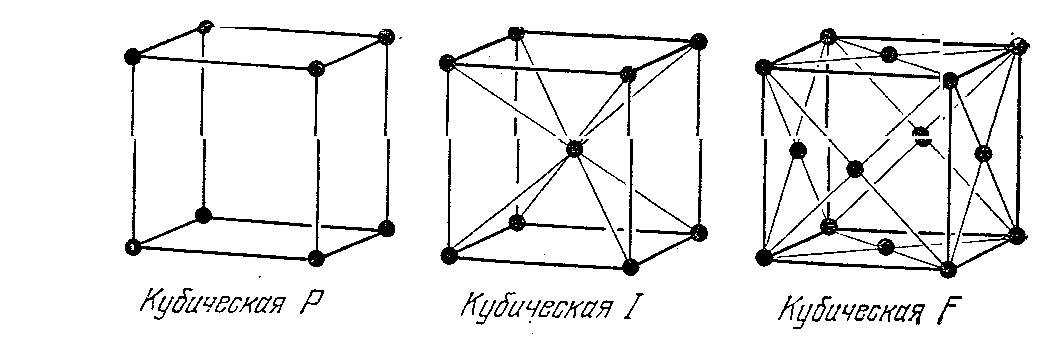
тип P имеет примитивную ячейку, тип С-ячейку с центрированными основаниями, тип I – объёмноцентрированную, т.е. буквально «внутрицентрированную» и, наконец, тип F – гранецентрированную.

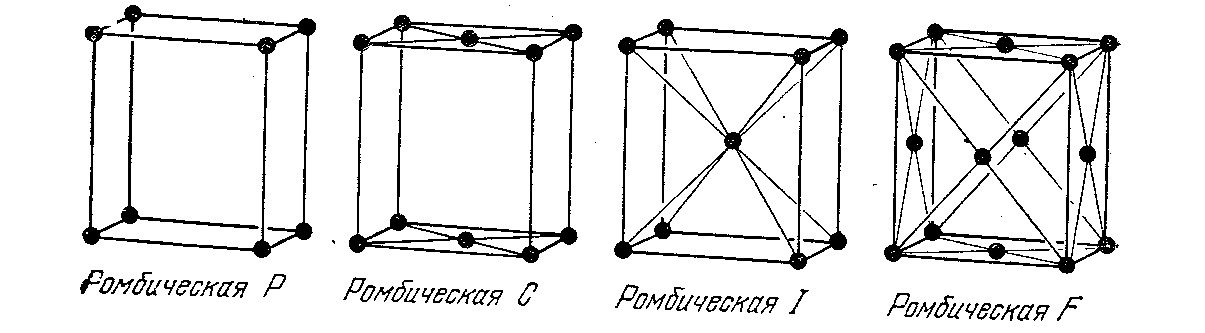
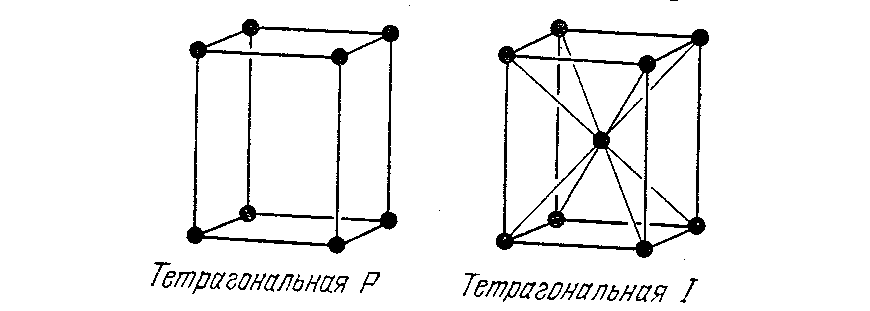
4) В тетрагональной системе простейшей ячейкой будет правильная призма с квадратом в основании. Эта ячейка примитивная, и поэтому решётка называется тетрагональной типа Р. Вторая тетрагональная ячейка типа I –объёмноцентрированная.

5) В кубической системе возможны три типа решётки: простая кубическая P с примитивной ячейкой, объёмноцентрированная I кубическая решётка (ОЦК) и гранецентрированная F кубическая решётка (ГЦК).

6) В тригональной системе в качестве элементарной ячейки обычно

выбирают ромбоэдр. Решётка является примитивной, но обозначают её обычно буквой R, а не P, и соответственно называют её тригональной пространственной решёткой типа R.

д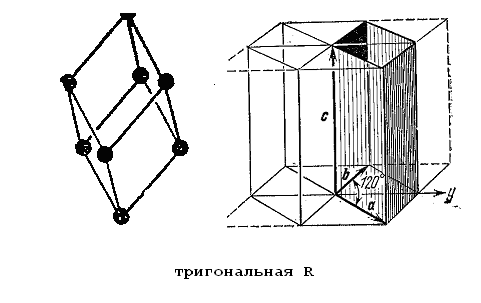 ля того чтобы подчеркнуть принадлежность данной элементарной ячейки к гексагональной системе, часто добавляют к ней ещё две ячейки, повёрнутые друг относительно друга на угол , получая, таким образом, утроенную ячейку в форме гексагональной призмы, имеющей в основании правильный шестиугольник.

Рассмотрим теперь симметрию направлений в кристалле. Совокупность всех поворотов, зеркальных поворотов, которые переводят каждое направление в кристалле в эквивалентное направление, образует точечную группу F , характеризующую симметрию направлений. Элементы этой группы не обязательно принадлежат группе симметрии кристалла, так как от них не требуется, чтобы они переводили все точки кристалла в эквивалентные точки.

Группу F можно охарактеризовать следующим образом. Всякий элемент g группы G кристалла, очевидно можно представлять в виде . Совокупность всех элементов , соответствующих элементам g, образует точечную группу. Эта точечная группа есть не что иное, как группа направлений F. Все кристаллы, имеющие одну и ту же группу направлений, образуют один кристаллический класс. Оказывается, что существует всего 32 группы направлений и, следовательно, 32 кристаллических класса. Каждый элемент группы F является в то же время элементом группы K, т.е. F содержится в K, следовательно, F является подгруппой группы K. Так как у семи групп, характеризующих сингонии, существует ровно 32 подгруппы, то и число различных классов равно 32.

Распределение кристаллических классов между сингониями

Сингонии	Классы
Триклинная…………...
Моноклинная…………
Ромбическая………….. Тетрагональная……….
Ромбоэдрическая……..
Гексагональная………..
Кубическая…………….

До сих пор мы рассматривали симметрию «пустых» решёток. Вернёмся теперь к рассмотрению симметрии кристалла.

Кроме подгруппы трансляций, пространственная группа содержит так же другие преобразования, вид которых обусловлен, во - первых, симметрией решётки Браве, во – вторых, симметрией компонентов кристалла, т. е. симметрией периодически повторяющееся совокупности частиц, образующей кристалл. Это обстоятельство часто приводит к тому, что не все преобразования, совмещающие узлы пустой решётки, совмещают также компоненты кристалла. Поэтому возможно, что точечная группа кристалла будет только подгруппой точечной группы пустой решётки. Вследствие этого, в группу симметрии кристалла необходимо, кроме целочисленных трансляций ввести и нецелочисленные трансляции. 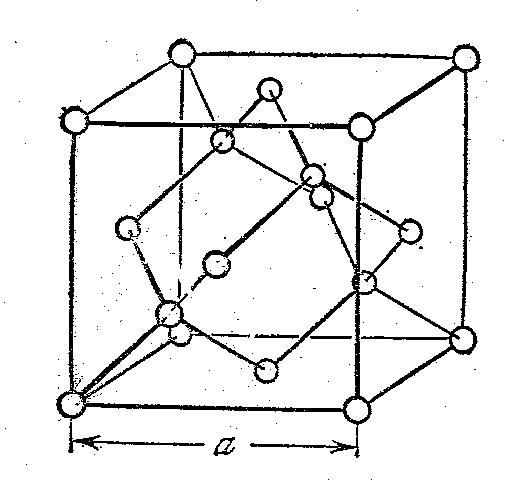Тогда общий элемент пространственной группы следует представлять в виде , где - некоторые преобразования из точечной группы K, а - т рансляции на вектор , отличный от вектора решётки. Для пояснения таких несобственных трансляций рассмотрим кристаллическую решётку алмаза. Её можно составить из двух гранецентрированных кубических решёток, сдвинутых друг относительно друга вдоль пространственной диагонали куба на ¼ её длины, при этом , где a-постоянная решётки (длина ребра куба).

Пространственные группы делятся ещё на симморфные и несимморфные. Симморфными называются такие группы, в которых после каждой операции симметрии из точечной группы F осуществляется трансляция на вектор решётки. Несимморфными группами являются группы с нецелочисленными трансляциями. Всего существует 230 пространственных групп. Эти 230 групп называют федоровскими по имени российского кристаллографа Фёдорова, открывшего их. Из них симморфными являются 73 группы, остальные несимморфные.