Предельное значение относительной погрешности
. (3.13)
Пример:
Цифровой частотомер с временем измерения
выполняет измерение сигналов с частотами
10МГц и 100Гц. Найти предельные значения
относительной погрешности квантования
,
меры
и суммарной погрешности
.
Относительная нестабильность частоты
кварцевого генератора
,
погрешностью преобразования пренебречь.
Решение:
Для сигналов с частотами
и
погрешность меры будет одинаковой и
составит
.
Относительная погрешность квантования
для сигнала с частотой
составит
,
для сигнала с частотой
.
Суммарная погрешность для первого сигнала составит:
,
для второго
.
Таким
образом, на низких частотах наблюдается
резкое увеличение погрешности измерения
частоты. Одним из способов повышения
точности является увеличение времени
измерения
.
Так, например, для F=100
Гц, чтобы
стало равной 10-7
необходимо обеспечить
с,
а это очень большой интервал времени.
Эффективным методом уменьшения погрешности квантования низкочастотных сигналов является переход в режим измерения периода.
Значение времени счета выбирают в К раз большим измеряемого периода T, что позволяет уменьшить погрешности квантования и преобразования.
Структурная схема цифрового измерителя периода имеет вид, приведенный на рис. 3.16. Эпюры напряжений, поясняющие принцип работы измерителя, приведены на рис. 3.17.
Измеренное значение периода определяется по формуле
,
где m=0, 1, 2, .., 8.
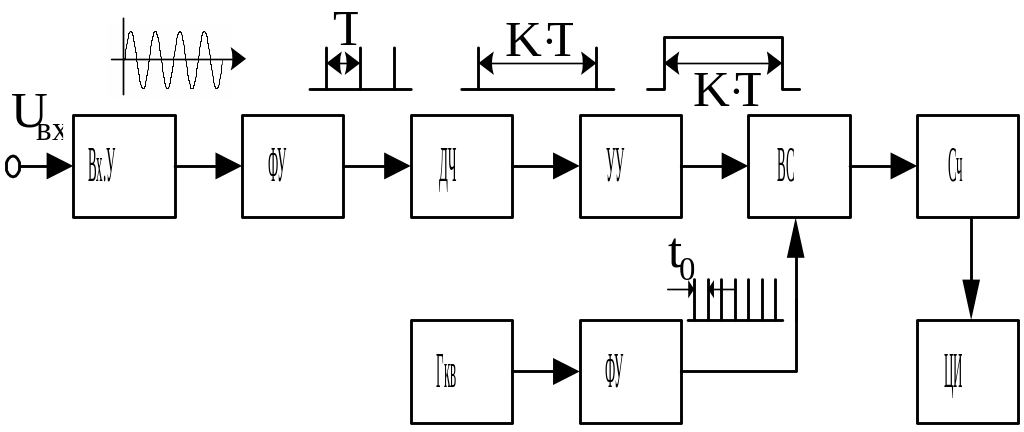
Рис. 3.16. Цифровой измеритель периода
Рис. 3.17. Эпюры напряжений
Таким
образом, цифровой измеритель периода,
так же как измеритель частоты, является
прямопоказывающим прибором, поскольку
значения периода следования импульсов
кварцевого генератора
и коэффициента деления частоты
выбраны кратными 10.
Как и при измерении частоты, при измерении периода имеют место погрешности меры, преобразования и квантования.
Погрешность меры. Абсолютная погрешность меры:
Относительная погрешность меры определяется так же как и в режиме измерения частоты
Погрешность квантования. Абсолютная среднеквадратическая погрешность квантования
Предельная погрешность квантования
.
Относительную среднеквадратическую погрешность квантования определяют как
,
.
Предельная относительная погрешность квантования
.
Погрешность преобразования. В отличие от режима измерения частоты, этой составляющей никак нельзя пренебречь, поскольку происходит измерение начала и конца временного интервала, которые могут флуктуировать по причине фазовых шумов.
Абсолютная погрешность преобразования
,
где 
— отношение сигнал/шум по напряжению;
K
– число усредняемых периодов входного
сигнала (коэффициент деления делителя
частоты).
Относительную погрешность преобразования находят как отношение абсолютной погрешности к величине измеренного периода:
.
Пример:
Найти значение погрешности квантования
для частоты
из предыдущего примера при переходе в
режим измерения периода для прежнего
времени измерения
с.
Решение:
Относительная погрешность меры при
переходе в режим измерения периода не
изменится и составит
.
Относительная погрешность квантования
составит
.
Суммарная погрешность измерения периода без учета погрешности преобразования
.
Таким
образом, погрешность квантования в
данном случае уменьшилась в
раз, при этом время измерения не
изменилось.