2. Цифровые фазометры

На рис. 2.16 приведена классификация цифровых фазометров (ЦФ) по принципу построения.

Рис. 2.16. Классификация цифровых фазометров

За рубежом получили распространение ЦФ с преобразованием фазового сдвига в напряжение ( ), которое затем измеряется цифровым вольтметром (ЦВ) (рис. 2.17).

Рис. 2.17. ЦФ с преобразованием фазовый сдвиг – напряжение

В нашей стране наибольшее распространение получили фазометры с преобразованием фазового сдвига в интервал времени ( ).

2.3.1. Цифровые фазометры с преобразованием фазового сдвига в интервал времени

Рассмотрим схемы преобразователей фазовых сдвигов в интервалы времени ( ).

• Схема однополупериодного преобразователя без исключения мертвой зоны триггера приведена в п. 2.2.3 на рис. 2.4, эпюры напряжений к ней – на рис. 2.5.

• Двухполупериодная схема без исключения мертвой зоны приведена на рис. 2.18. Результат измерения ФС:

,

где .

• Двухполупериодная схема с исключением мертвой зоны приведена в п. 2.2.4 на рис. 2.7, эпюры напряжений к ней – на рис. 2.8.

Независимо от вида измерительного преобразователя цифровое измерение ФС основано на измерении интервалов и T цифровым методом. Значение ФС находят как:

(2.26)

Рис. 2.18. Двухполупериодный преобразователь без исключения мертвой зоны

Погрешность определения ФС обусловлена погрешностью цифрового метода измерения интервалов времени и T. Если считать, что погрешность измерения периода T пренебрежимо мала по сравнению с погрешностью измерения интервала , то

, (2.27)

где F – частота входного измеряемого сигнала; − частота квантующих импульсов.

Пример: Цифровой измеритель фазового сдвига с преобразованием ФС в интервал времени. Частота квантующих импульсов =10 МГц, частота входного сигнала F=1 МГц. Найти погрешность измерения ФС.

Решение: Погрешность измерения ФС определяется по формуле (2.27):

.

Таким образом, погрешность измерения ФС на высоких частотах является недопустимо большой.

2.3.2. Цифровые фазометры со временем измерения, кратным периоду

Уменьшить значение погрешности квантования можно путем измерения и в K периодах входного сигнала и последующего усреднения результатов.

В этом случае значения и T находят как средние арифметические наблюдаемых значений и :

,

, (2.28)

где − число импульсов, попавших в интервалы и ; ; − суммарное число импульсов, зафиксированное в K периодах входного сигнала.

С учетом усреднения K результатов измерений, значение ФС определим по формуле

. (2.29)

Погрешность ФС, найденного путем усреднения K результатов измерения уменьшится в раз по сравнению с погрешностью ФС, найденного без усреднения

. (2.30)

Формула (2.27) является частным случаем выражения (2.30) при K=1. Определение ФС в соответствии с (2.29) требует применения в фазометре микропроцессорного вычислительного блока (МВБ).

Фазометры, реализующие алгоритм вычисления ФС в соответствии с (2.29), называются ЦФ с временем измерения, кратным периоду. На рис. 2.19 приведена структурная схема такого ЦФ, в соответствии с которой создан отечественный фазометр ФК2-35.

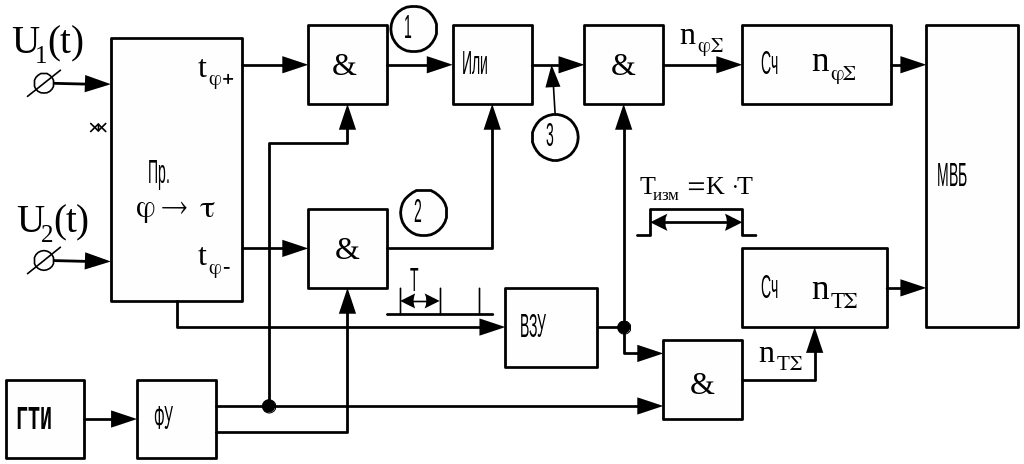Рис. 2.19. ЦФ с временем измерения, кратным периоду

Эпюры напряжений в точках схемы рис. 2.19. приведены на рис. 2.20. Сигналы с выхода ФУ от ГТИ сдвинуты друг относительно друга на время для того, чтобы на выходе элемента "ИЛИ" они воспринимались как раздельные.

Времязадающее устройство (ВЗУ) формирует интервал измерений . В итоге счетчик подсчитает общее число импульсов за время измерения. Число , пропорциональное интервалу , определяется как .

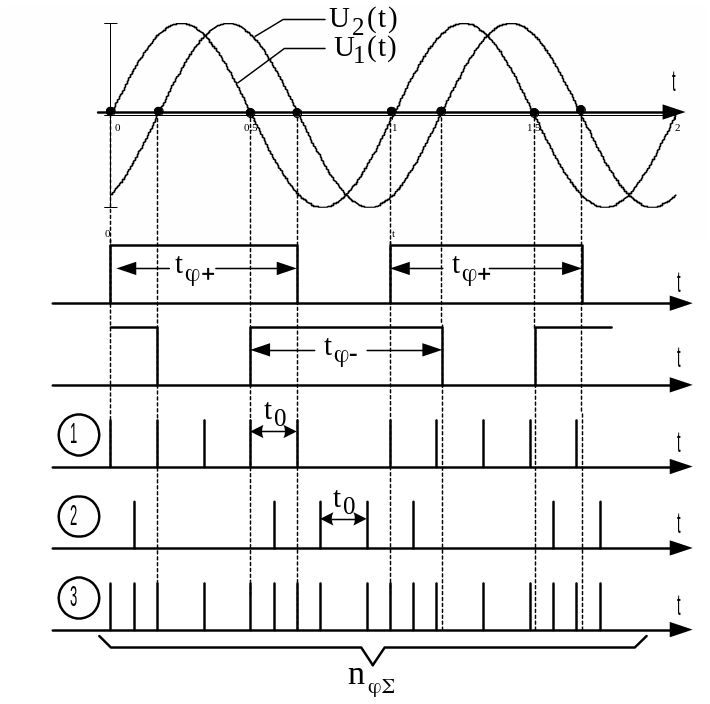
Рис. 2.20. Эпюры напряжений в ЦФ с временем измерения, кратным периоду

МВБ осуществляет оценку ФС по формуле

. (2.31)

Время измерения составляет K периодов входного сигнала, т. е. оказывается кратным периоду.

Пример: Цифровой измеритель фазового сдвига со временем измерения, кратным периоду. Частота квантующих импульсов =10 МГц, частота входного сигнала F=1 МГц, время измерения =1 с. Найти погрешность измерения ФС.

Решение: Число усредняемых периодов входного сигнала составляет

.

Погрешность измерения ФС определяется по формуле (2.27):

.

По сравнению с предыдущим примером погрешность измерения ФС уменьшилась в 1000 раз.

К недостаткам ЦФ со временем измерения, кратным периоду, относится необходимость выполнения арифметических операций. До применения микропроцессорных БИС этот недостаток сдерживал развитие данных ЦФ.

Для того чтобы избежать выполнения операции деления при вычислении по формуле (2.26), разработаны ЦФ с постоянным временем измерения. Данные ЦФ реализуются на жесткой логике и не требуют применения микропроцессорных БИС.