Корреляционный фазометр
При
измерении фазового сдвига между
напряжениями
и
может быть использована их
взаимокорреляционная функция (ВКФ). ВКФ
сигналов
и
запишется в виде
,
(2.11)
Значение
ВКФ зависит от величины фазового сдвига
между напряжениями и максимально при
.
Значение
можно определить как
(2.12)
На
рис. 2.9 приведена зависимость
от величины фазового сдвига
.
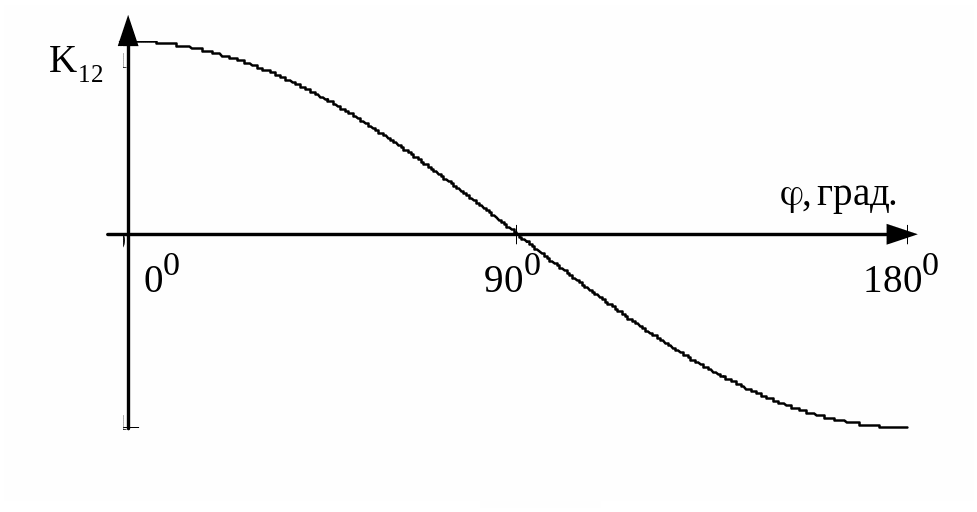
Рис.
2.9. Зависимость
от фазового сдвига
Структурная схема корреляционного фазометра, выполняющего оценку в соответствии с формулой (2.12), приведена на рис. 2.10.
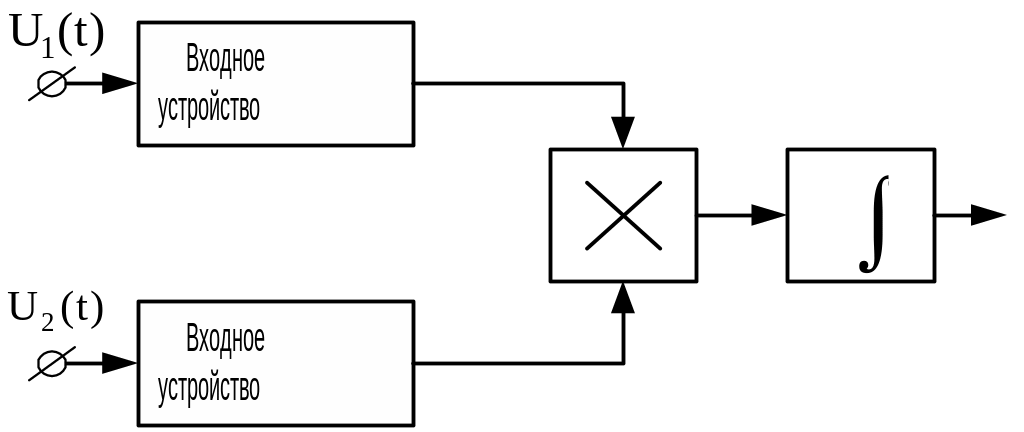
Рис. 2.10. Структурная схема корреляционного фазометра
Корреляционным методам измерения фазовых сдвигов присущи следующие недостатки:
Необходимость выполнения арифметических операций, наличие нелинейных элементов (перемножитель);
Зависимость показаний от амплитуд входных сигналов
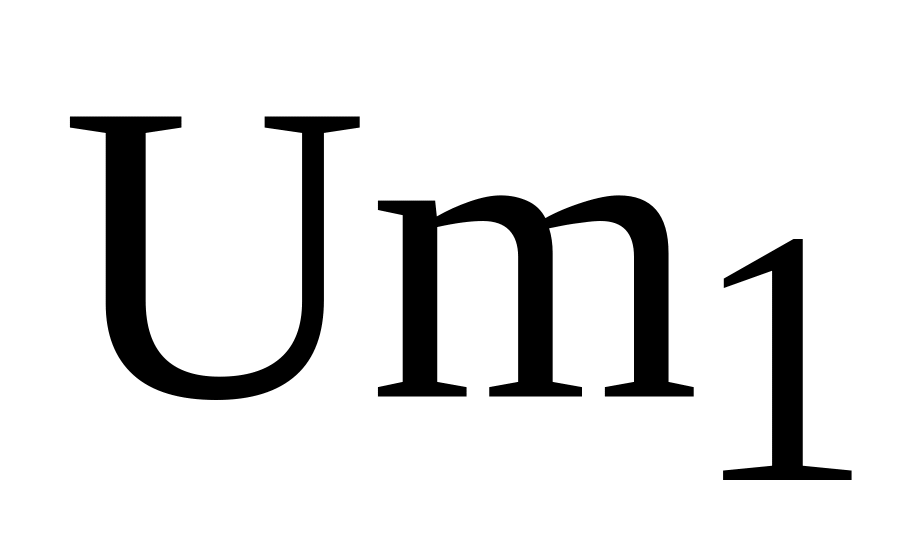и
.
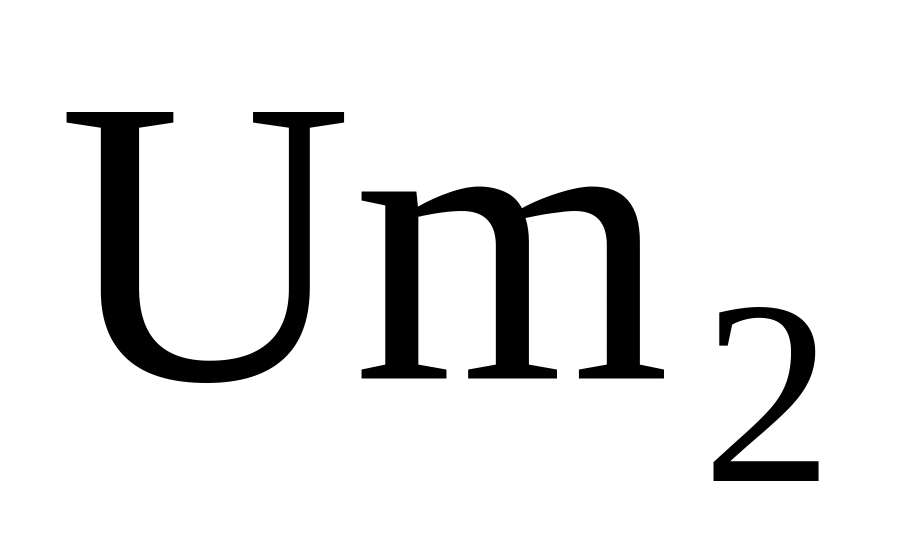Достоинством данного фазометра является высокая помехоустойчивость и возможность работы при малых отношениях сигнал/шум.
Оптимальные фазоизмерители
Очень
часто на практике возникает необходимость
измерения ФС при работе в широком
диапазоне отношений сигнал/шум q,
в том числе и для
и q<<1.
Особенно остро потребность в таких
методах и устройствах ощущается при
создании приемной аппаратуры современных
фазовых радиогеодезических и
радионавигационных систем, где значение
фазового сдвига является одним из
важнейших параметров сигнала, с
использованием которого решаются задачи
определения координат объектов.
Задачу создания помехоустойчивых фазоизмерителей, работающих в широком диапазоне отношений сигнал/шум, можно решить на основе оптимальных методов, обеспечивающих минимальную погрешность при воздействии флуктуационных помех. Одним из этих методов является метод максимума функции правдоподобия.
Рассмотрим метод максимального правдоподобия применительно к нахождению оптимальной оценки ФС сигнала, искаженного гауссовым шумом.
Имеется
сигнал
.
Фаза сигнала
неизвестна и подлежит измерению. Прием
сигнала происходит на фоне аддитивной
помехи
.
Для того чтобы найти оптимальную
процедуру измерения фазы, необходимо
получить функцию правдоподобия и найти
оценку фазы
,
максимизирующую ее.
Многомерная условная функция распределения смеси сигнала и помехи имеет вид
,
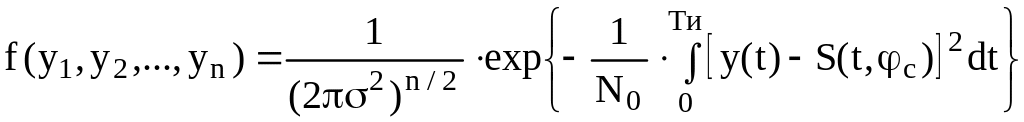(2.13)
где
у(t)
– конкретная реализация смеси полезного
сигнала
и помехи
;
независимые
отсчеты входного процесса за время
измерения
;
n
– общее число отсчетов;
,
спектральная плотность мощности и
дисперсия помехи
соответственно.
Полученное выражение содержит зависимость от и может рассматриваться как функция правдоподобия
.
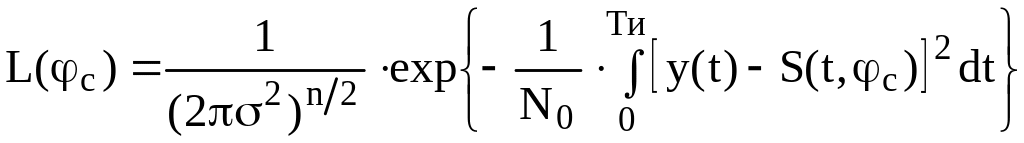(2.14)
Для того, чтобы представить эту функцию в более удобной форме, позволяющей найти оценку, соответствующую максимуму правдоподобия, произведем преобразование (2.14) к следующему виду
.
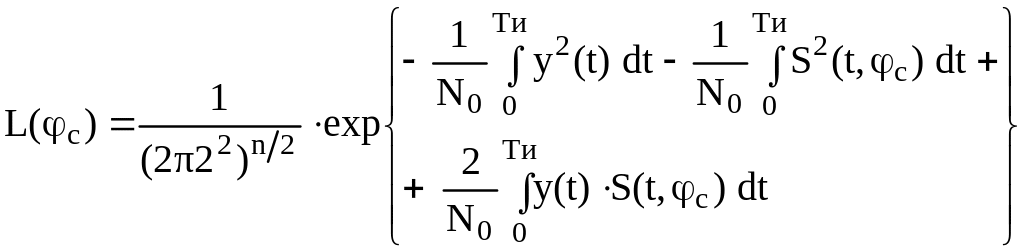(2.15)
Поскольку
,
и
считаются известными, то:
;
,
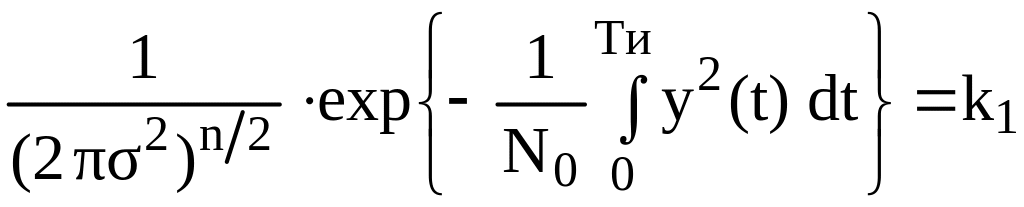(2.16)
где
– постоянный коэффициент;
− энергия сигнала, накопленная за время
измерения
.
Подставив
(2.16) в выражение для
,
получим:
.
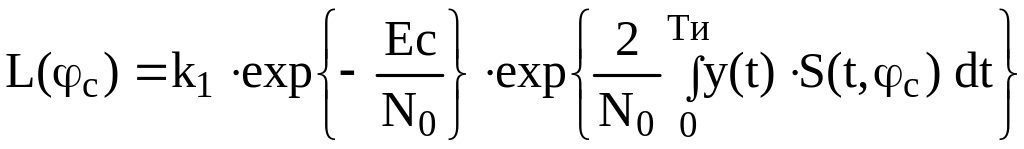(2.17)
Оптимальная
оценка ФС сигнала
должна приводить функцию правдоподобия
(2.17) в максимум. Следовательно, для
нахождения оптимальной оценки ФС,
необходимо найти максимум функции
правдоподобия.
Решение
задачи нахождения оптимальной оценки
ФС приведено, например в [3, c.
376] , где показано, что при гармоническом
сигнале
оптимальную оценку ФС сигнала
принятого на фоне шума
,
можно найти как:
,
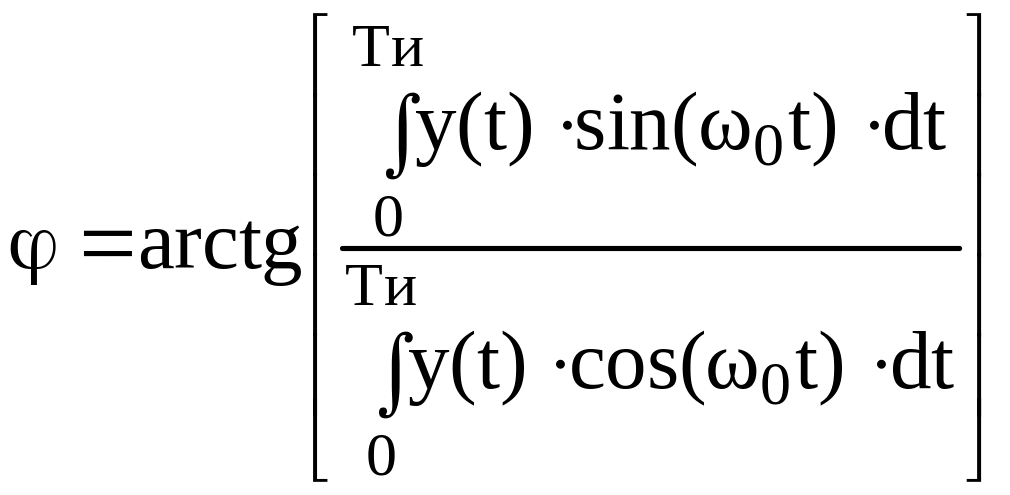(2.18)
В соответствии с выражением (2.18) для оптимальной оценки ФС получена структурная схема ортогонального фазоизмерителя, приведенная на рис. 2.11.
На выходе фазометра формируется оценка ФС гармонического опорного сигнала по формуле:
,
(2.19)
где
,
− синфазная и квадратурная составляющие
входного сигнала.
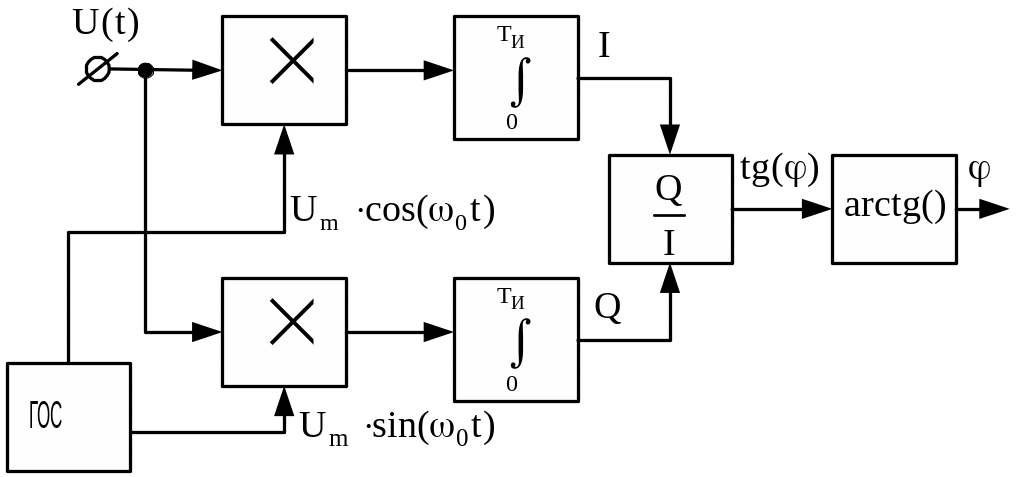
Рис.2.11. Структурная схема ортогонального фазоизмерителя
Можно показать, что погрешность оценки ФС ортогональным фазоизмерителем определяется выражением
(2.20)
и
не зависит от способа модуляции
измеряемого сигнала
.
Полученный результат показывает, что погрешность оценки ФС зависит только от отношения плотности мощности помех к энергии сигнала. Сигнал может быть промодулирован любым способом – по амплитуде или фазе (частоте), и если модуляция известна и воспроизведена в копии сигнала, то погрешность результата измерения будет зависеть только от энергии сигнала. Следовательно, сигнал может быть сложным, (т. е. состоять из последовательности импульсов (пачки) с разной формой огибающей каждого импульса и пачки в целом,) или шумоподобным, (т. е. сложно модулированным по фазе; точность измерения фазы от этого не изменяется, если законы модуляции известны и воспроизведены в копии). Шумоподобные сигналы часто применяются в радионавигационных системах с целью обеспечения высокой помехоустойчивости и скрытности работы.