Формула Бернулли и наивероятнейшее число наступлений события.
Если проводится
независимых испытаний, в каждом из
которых вероятность наступления события
одна и та же
,
то вероятность того, что в
независимых испытаниях событие
наступит ровно
раз обозначается
и вычисляется по формуле Бернулли
,
где
Такая последовательность испытаний называется схемой Бернулли. Наступление события в одном испытании обычно называют успехом, а не наступление – неудачей. Вероятности носят название биномиальные вероятности.
Рассмотрим частные
случаи
=
,
=
,
.
Вероятности того, что в
испытаниях событие наступит
менее раз: + +…+
.более раз:
+
+…+
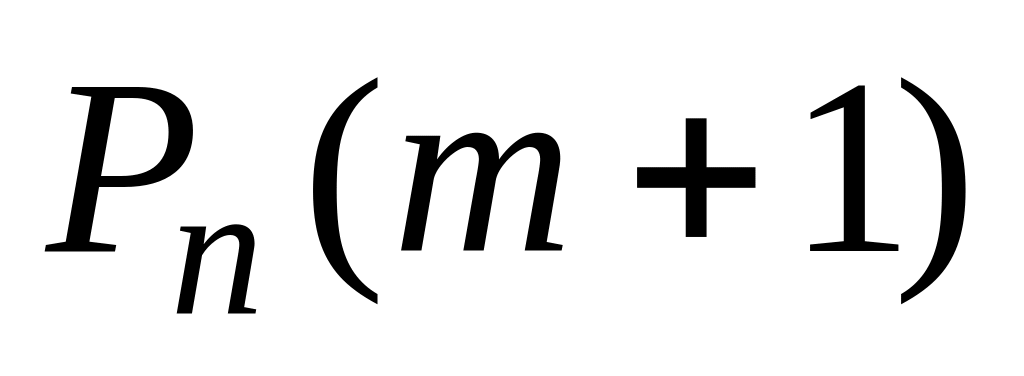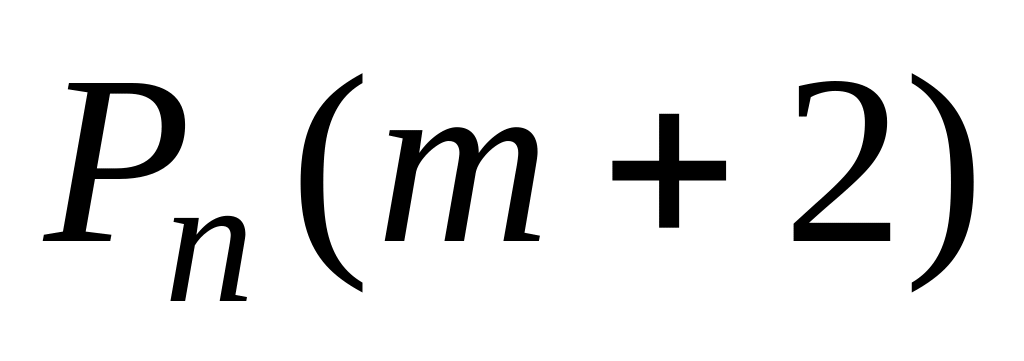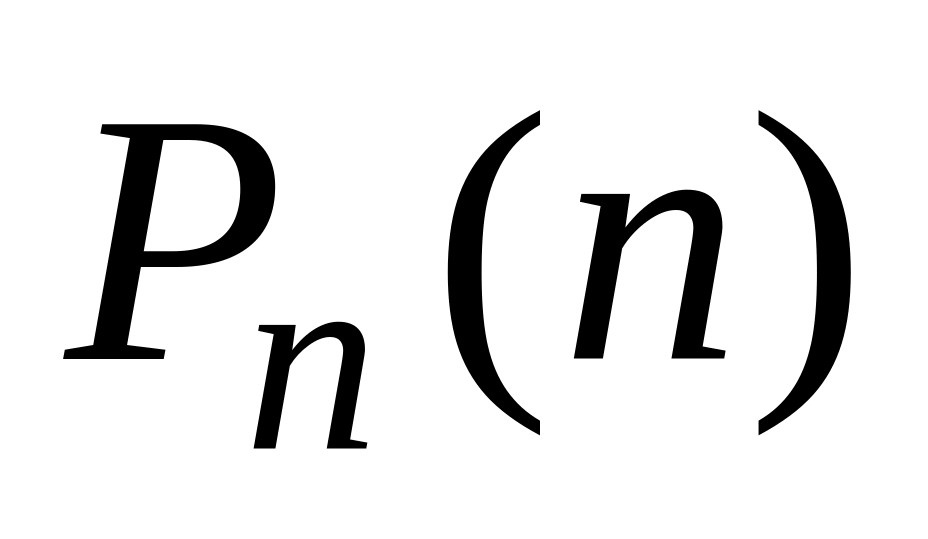.не менее раз:
+
+…+
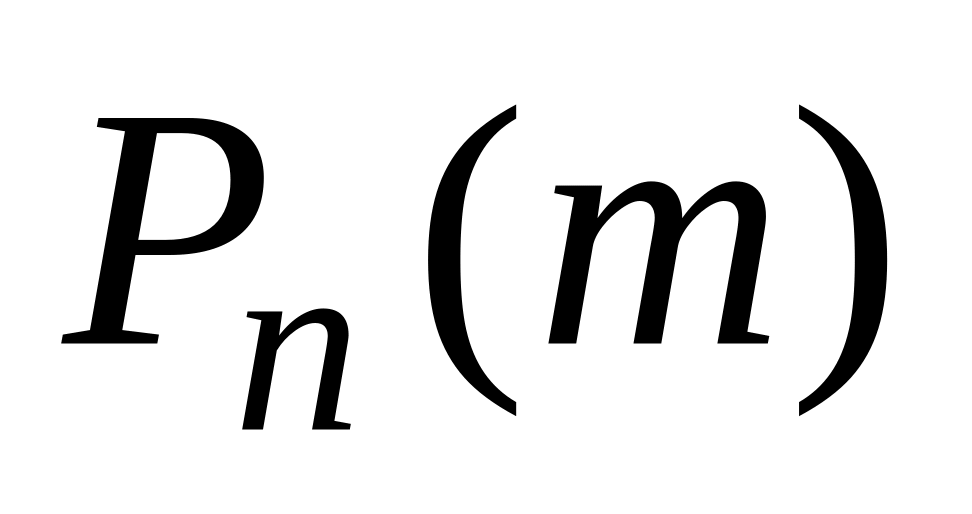.не более раз: + +…+ .
Пример 9. В магазин вошли 9 покупателей, участвующих в социологическом опросе. Вероятность сделать покупку для каждого вошедшего одна и та же и равна 0,2. Найти вероятность того, что ровно 2 покупателя совершат покупку.
Решение.
Из условия n=9;
k=2;
p=0,2;
q=1-0,2=0,8.
По формуле Бернулли искомая вероятность
Наивероятнейшее число наступления события.
Для каждого числа
наступления события мы можем подсчитать
биномиальные вероятности
,
,
…,
.
Число наступления события, которому при заданном соответствует самая большая среди всех вероятностей , называется наивероятнейшим числом наступления события . Обозначим это число через 0. Оно удовлетворяет неравенству
.
Замечание.
Если
– целое число, то наивероятнейших чисел
два:
и
.
Пример 10.
Вероятность
попадания в цель при каждом выстреле
из лука равна
.
Производится шесть выстрелов. Каково
наивероятнейшее число попаданий?
Решение.
В данном примере число выстрелов
.
Рассмотрим событие
.
.
Для этого события
известна вероятность
и, следовательно, вероятность
противоположного события, т.е. промаха
.
Для ответа на вопрос вычисляем
,
.
Следовательно
.
Единственное целое число, принадлежащее
этому отрезку –
.
Асимптотические формулы для вычисления биномиальных вероятностей.
При больших и пользоваться формулой Бернулли практически не возможно. В таких случаях пользуются локальной теоремой Лапласа или теоремой Пуассона. Эти формулы тем точнее, чем больше.
Локальная теорема Лапласа.
Если вероятность
наступления событий
не очень мала, а
велико (число успехов
в этом случае тоже растет с ростом
),
то имеет место локальная теорема Лапласа
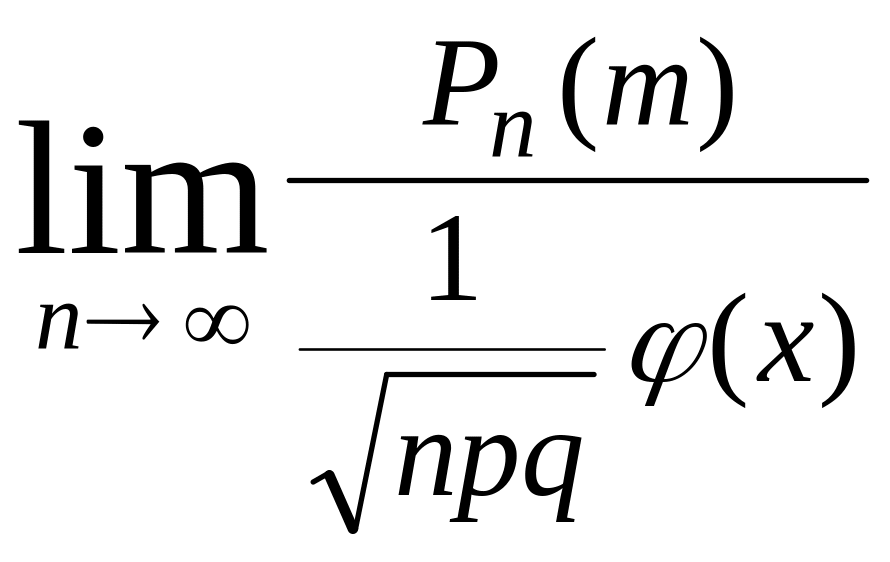=1.
Отсюда имеем приближенное равенство
,
где
и
‑ называется функцией
Гаусса.
З
начения
этой функции находят из таблицы, пользуясь
свойствами
Пример 11. Вероятность найти белый гриб среди прочих равна 0,25. Какова вероятность того, что среди 80 грибов белых будет 20?
Решение.
По условию
,
.
Следовательно,
и
.
Тогда искомая вероятность:
.
Формула Пуассона.
Пусть теперь вероятность наступления событий очень мала (<0,01), а велико (>100), то мы имеем дело с редкими явлениями, и будем пользоваться теоремой Пуассона
,
где
-
постоянная
Пример 12. На базу отдыха прибыло 1000 подростков. Какова вероятность того, что среди этих отдыхающих окажется 5 детей, страдающих клаустрофобией, если в среднем 0,1 % подростков страдают данной болезнью?
Решение. Из условия следует, что n=1000; р=0,001. Так как n – велико, а р – мало, то воспользуемся формулой Пуассона. Имеем
.
Тогда.
.