5. Вынужденные механические колебания. Явление резонанса.

Вынужденные колебания – незатухающие колебания системы, ко­торые вызываются действием на нее внешней периодически изменяющей­ся силы

.

В системе через некоторое время τ устанавливаются гармонические колебания с циклической частотой Ω вынуждающей силы. τ – время установления колебаний

,

где Δφ – сдвиг фаз между смещением и вынуждающей силой. Колебания системы отстают от колебаний вынуждающей силы (знак «-» перед Δφ).

З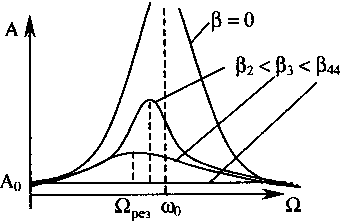 ависимость амплитуды от частоты вынуждающей силы для различ­ных коэффициентов затухания (β – коэффициент затухания, характеризующий скорость убы­вания амплитуды):

Если частота вынуждающей силы равна 0 (действует постоянная сила) то

При отсутствии затухания (β=0 и при Ω=ω₀ амплитуда колебаний стремится к бесконечности. Если затухание есть, то максимум амплитуды наблюдается при частоте Ω_рез (резонансная частота), не совпадающая с частотой собственных колебаний ω₀.

.

При Ω= Ω_рез наблюдается явление резонанса – явление резкого возрастания ампли­туды вынужденных колебаний. Форма резонансных кривых зависит от величины коэффициента затухания β.

Вынужденные колебания могут возникать при самых разнообразных условиях.

Параметрические колебания возникают при изменении собственных параметров системы. Например, в случае маятника можно изменять длину нити по заданному закону l=l(t) или, поднимая точку подвеса в неоднородном поле тяжести, изменять ускорение свободного падения.

Автоколебания. В незамкнутой системе работа сил трения может быть положительной величиной. В этом случае амплитуда колебаний будет возрастать и в установившемся режиме примет постоянное значение. Если незатухающие колебания поддерживаются в результате поступления энергии от постоянного источника, то такие системы называются автоколебательными. Колебания скрипичной струны при равномерном движении смычка, маятника в настенных часах – примеры автоколебаний.

6. Распространение колебаний в упругих средах. Поперечные и продольные волны. Длина волны. Связь между длиной волны, скоростью ее распространения и периодом (частотой).

Механическая волна – процесс распространения колебаний в упругой среде.

Способность газа сопротивляться изменению объема – объемная упругость газа. Газы легко изменяют свою форму, т.е. не обладают упругостью формы.

Упругая среда состоит из большого числа связанных друг с другом частиц, совершающих колебания и называемых вибраторами.

Если возбуждаются колебания одной из частиц, то она становится центром распространяющейся волны.

Волны, в которых происходит перемещение фазы с определенной скоростью, называются бегущими.

При наблюдении за волнами видно именно распространение фазы, например, движение гребня волны. Скорость распространения фазы волны называется фазовой скоростью. Все точки среды в волне колеблются около своего положения равновесия и вместе с фазой не перемещаются.

Кинематическим признаком волнового движения служит распространение фазы колебаний, динамическим – перенос энергии. Характер механических волн, распространяющихся в среде, зависит от упругих свойств этой среды.

1. Поперечные – волны, в которых колебания частиц среды происходят перпенди­кулярно к направлению распространения волны.

направление колебаний

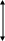
направление распространения волны

Поперечная волна возникает в результате деформации сдвига, следствием которой является изменение формы тела. Она может возникнуть только в твердых телах или на поверхности жидкости.

2. Продольные волны – волны, у которых направление колебаний частиц совпадает с направлением распространения волны. Они возникают в результате деформации сжатия и разрежения.

н аправление колебаний

н аправление распространения волны

Направление распространения волны называют лучом.

Возникновение продольных волн возможно в твердых телах, жидкостях и газах.

В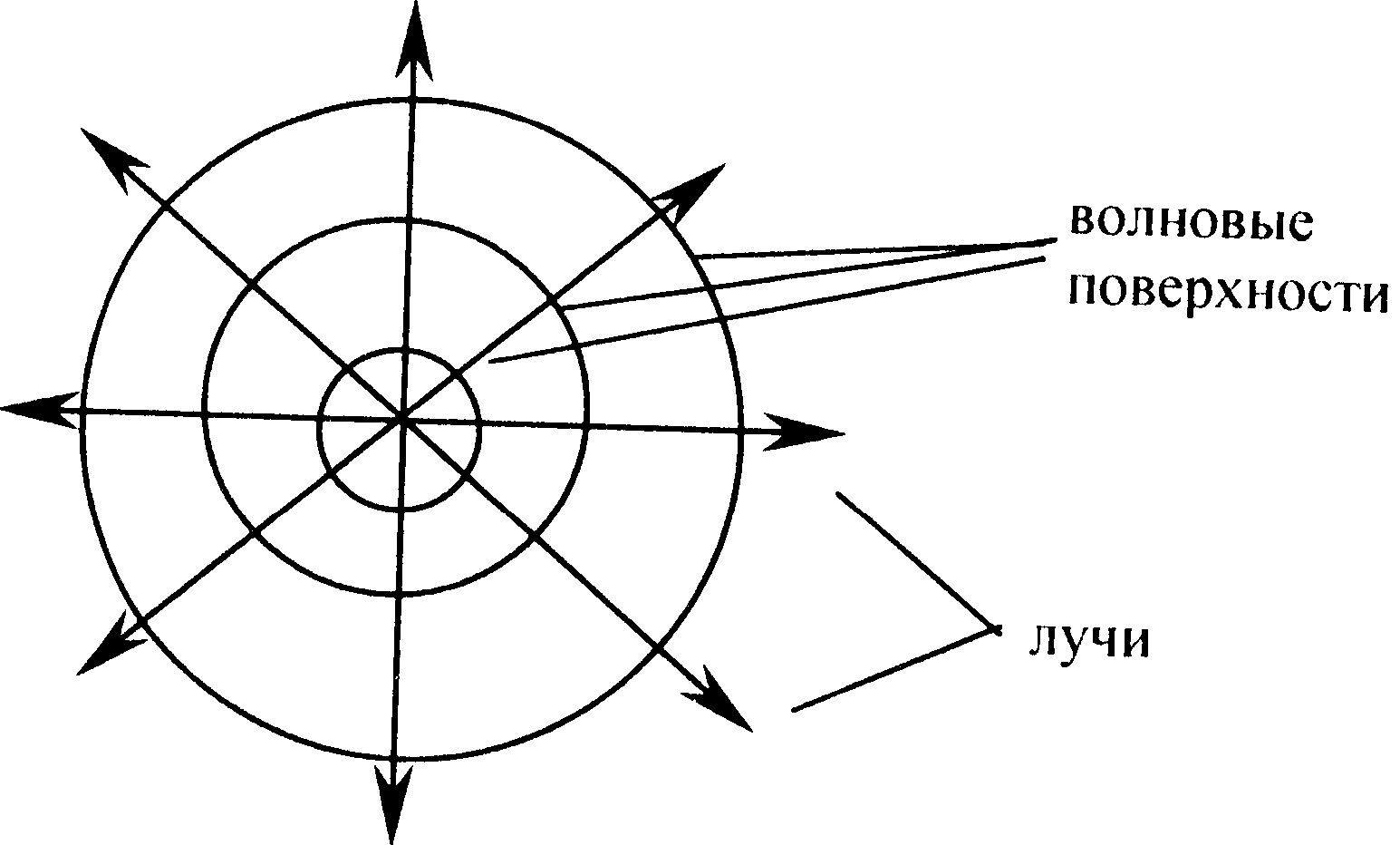 олновой поверхностью называется геометрическое место точек, колеблющихся с одинаковой фазой. В изотропной среде луч перпендикулярен волновой поверхности.

У волн, распространяющихся из точечного центра возбуждения, лучи направлены радиально, а волновые поверхности представляют собой сферы.

В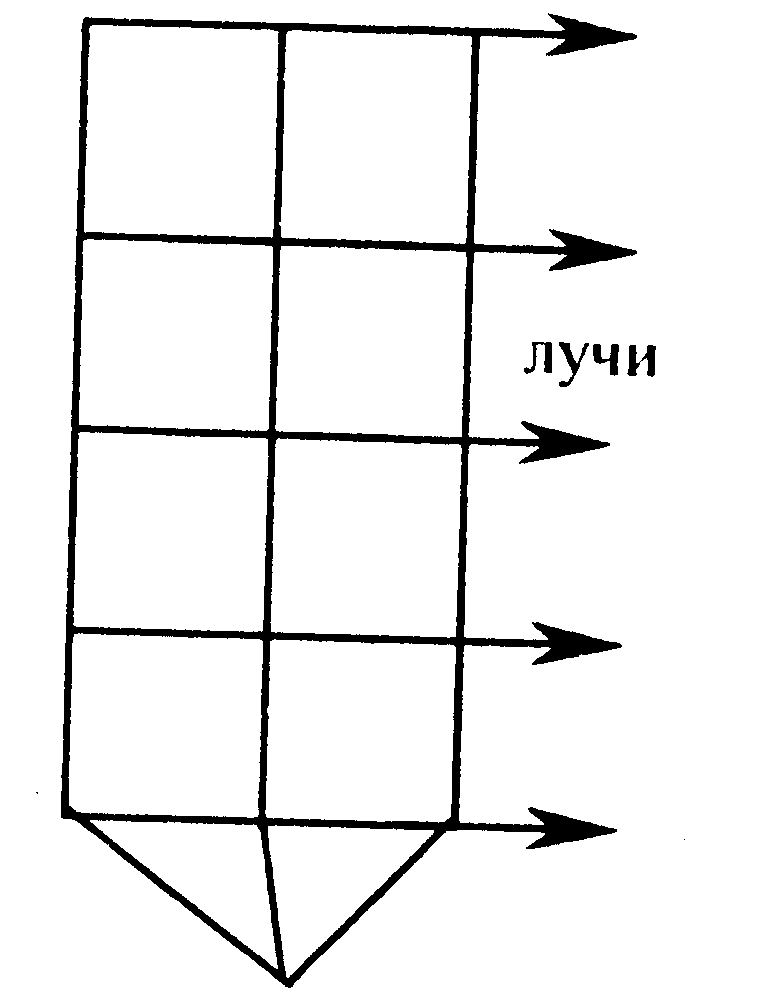 случае плоского источника возникают плоские волны. В них лучи параллельны, а волновые поверхности представляют собой плоскости.

Расстояние между соседними волновыми поверхностями называется длиной волны λ. Длина волны не зависит ни от координаты, ни от времени.

Длина волны λ – расстояние между точками, колеблющимися с одинаковой фазой.

Продолжительность полного колебания частицы - период ,

где v - частота колебаний.

За один период волна распространяется на расстояние, равное длине волны λ:

,

где ω – круговая частота.

Скорость распространения волны – фазовая скорость: .

Фазовая скорость зависит от механических свойств среды.

Упругие волны с большой амплитудой – ударные, с малыми амплитудами – звуковые.

Уравнение плоской волны

Если в источнике волн изменение колеблющейся величины (откло­нение) происходит по закону: ,

то в точку, расположенную на расстоянии х от источника, волна придет запаздыванием .

– уравнение плоской синусоидальной волны, распространяю­щейся вдоль оси х .

Величина называется волновым числом. Оно показывает, сколько длин волн укладывается на расстоянии, равном 2π единиц длины.

Тогда уравнение плоской волны примет вид: .

Эта волна распространяется в положительном направлении оси х. При распространении волны в обратном направлении