Колебание груза на пружине.
При действии на тело внешней силы Fвн пружина растягивается и по третьему закону Ньютона появляется возвращающая сила упругости Fynp, действующая на пружину и равная
,
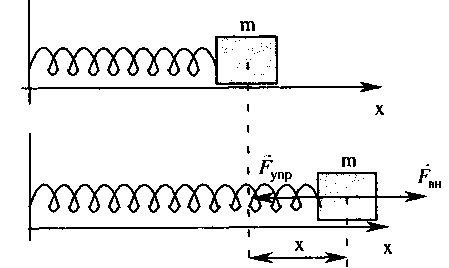
где k – коэффициент жесткости пружины, х – деформация пружины. Знак «-» показывает, что Fynp и х направлены противоположно. По второму закону Ньютона:
Собственная частота колебаний пружинного маятника:
.
Период собственных колебаний пружинного маятника:
.
С
обственными
свободными колебаниями называются
колебания, происходящие под действием
силы тяжести или силы упругости,
являющимися внутренними силами.
Уравнение движущегося
тела, совершающего гармонические
колебания:
.
Решение этого уравнения: .
где А – максимальное отклонение тела от положения равновесия.
Математический маятник.
Математический маятник – это материальная точка, подвешенная на невесомой нерастяжимой нити и совершающая движение в вертикальной плоскости под действием силы тяжести. Колебания маятника будут гармоническими, если угол отклонения а не превышает 8 градусов.
На материальную
точку (шарик) действуют сила тяжести
и сила натяжения нити
.
Действие этих сил приводит к движению
шарика по окружности радиуса l
с полным ускорением
:
(1).
П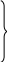
оскольку
направление и величина скорости шарика
изменяются то ускорение имеет две
составляющие: нормальную
(центростремительную)
,
и тангенциальную
(касательную) к окружности
.
Следует учесть, что результирующая сил
и
всегда направлена к центру окружности.
Проектируя уравнение (1)
на прямую, проходящую через шарик и
точку подвеса и прямую, касательную к
окружности, получаем (при малых углах
):
Собственная частота колебаний математического маятника:
.
Период собственных колебаний математического маятника:
.
Свойства колебаний математического маятника:
при малых углах колебаний период колебаний математического маятника не зависит ни от амплитуды колебаний, ни от массы маятника;
период колебаний математического маятника прямо пропорционален корню квадратному из длины маятника l и обратно пропорционален корню квадратному из ускорения свободного падения g (позволяет измерять ускорение свободного падения, его зависимость от высоты и определять местные искажения гравитационного поля).
Если маятник
находится в системе отсчета, которая
движется с ускорением а
(неинерциальная
система отсчета), выражение для периода
колебания остается тем же, но ускорение
свободного падения заменяется на
эффективное ускорение:
.
Преобразование энергии при гармоничных колебаниях.
Энергия системы,
колеблющейся без затухания, остается
постоянной. Она складывается из
потенциальной энергии
и кинетической
энергии. Величины этих обеих энергий
меняются периодично. В каждый момент
времени полная энергия:
;
;
.
В процессе колебаний потенциальная энергия превращается в кинетическую и наоборот. При этом полная энергия остается постоянной. Процесс перехода одного вида энергии в другой носит периодический характер.
В точке поворота и при прохождении положения равновесия энергия одного вида равна нулю, в то время как значение другой достигает максимума.