Колебания и волны Механические колебания и волны

Колебательное движение. Свободные механические колебания. Гармоничные колебания. Смещение, амплитуда, период, частота и фаза гармоничных колебаний. Колебание груза на пружине. Математический маятник. Преобразование энергии при гармоничных колебаниях. Вынужденные механические колебания. Явление резонанса.

Распространение колебаний в упругих средах. Поперечные и продольные волны. Длина волны. Связь между длиной волны, скоростью ее распространения и периодом (частотой).

Звуковые волны. Скорость звука. Громкость звука и высота тона. Інфра- и ультразвуки.

1. Колебательное движение. Свободные механические колебания. Гармоничные колебания. Смещение, амплитуда, период, частота и фаза гармоничных колебаний.

Колебательным движением называется движение, при котором состояние движущегося тела обладает той или иной степенью повторяе­мости во времени. Любое колебание – это движение с переменным ускоре­нием; отклонение, скорость и ускорение в этом случае зависят от времени.

Свободными называют колебания, происходящие под действием внутренних сил системы, энергия колебаний в этом случае не восполняется (затухающие колебания)

Вынужденными называют колебания, происходящие под действием внешней периодической силы при постоянном восполнении энергии.

Гармонические колебания – это колебания, при которых колеблющаяся физическая величина изменяется по закону синуса или косинуса.

Гармонические колебания можно представить в виде проекции на некоторую ось радиус-вектора , проведенного из точки О под углом φ₀, равным начальной фазе и вращающимся с угловой частотой ω вокруг этой точки. Если изобразить графически колебания на диаграмме отклонение-время, то получится синусоидальная кривая (здесь φ₀ =0).

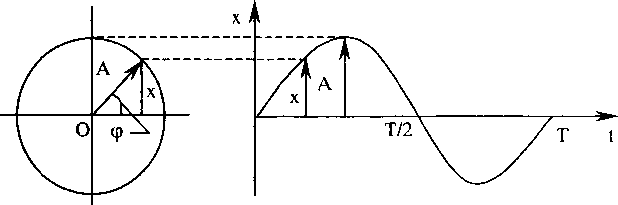
Уравнение кривой:

Если рассматривать начало колебаний в точке, где отклонение максимально, то уравнение колебаний станет:

.

Период – скалярная физическая величина, характеризующая время одного полного колебания (время, через которое параметры системы повторяются).

В системе SI: .

Частота – скалярная физическая величина, характеризующая число колебаний в единицу времени: ,

В системе SI: (герц).

Угловая (циклическая) частота – скалярная физическая величина, характеризующая число колебаний за время 2π секунд: .

В системе SI: .

Смещение или отклонение х = f(t) – мгновенное значение перемеще­ния относительно положения равновесия.

Амплитуда (А) – скалярная физическая величина, модуль максимального отклонения от положения равновесия, размах колебаний.

Фаза – скалярная физическая величина, характеризующая состояние колебательной системы в данный момент времени (аргумент тригонометрической функции в уравнении колебаний): (выражается в радианах).

Начальная фаза φ₀ – значение фазы при t = 0 (начало колебаний).

Скорость при гармонических колебаниях:

(или ),

где – максимальное значение скорости.

Преобразовав фазу скорости, получим и : скорость опережает по фазе смещение на четверть периода (см. рис.).

Ускорение при гармонических колебаниях не постоянно, а зависит от времени:

где – максимальное значение ускорения.

Если смещение х изменяется по гармоническому закону, то модуль ускорения всегда пропорционален абсолютному значению х, а направление ускорения всегда противоположено направлению изменения х: .

Преобразовав ускорение к виду , получаем, что фаза ускорения опережает фазу смещения х на π (см. рис.).

Отличительным признаком гармоничес­ких колебаний является пропорциональность возвращающей силы сме­щению.