Для задач.

1. Пути, пройденные телом из состояния покоя ( ) за равные последовательные промежут­ки времени, относятся как ряд последовательных нечетных чисел: .

2. Путь, пройденный телом в последнюю секунду движения из состояния покоя ( ), где п – число секунд, t = 1:

3. Свободным падением называют движение под действием только силы тяжести. Оно является равноускоренным движением с ускорением, не за­висящим от массы.

4. У поверхности Земли ускорение свободного падения приблизительно равно: g = 9,81 м/с².

5. Уравнения свободного падения (ось Оу направлена вниз из точки падения):

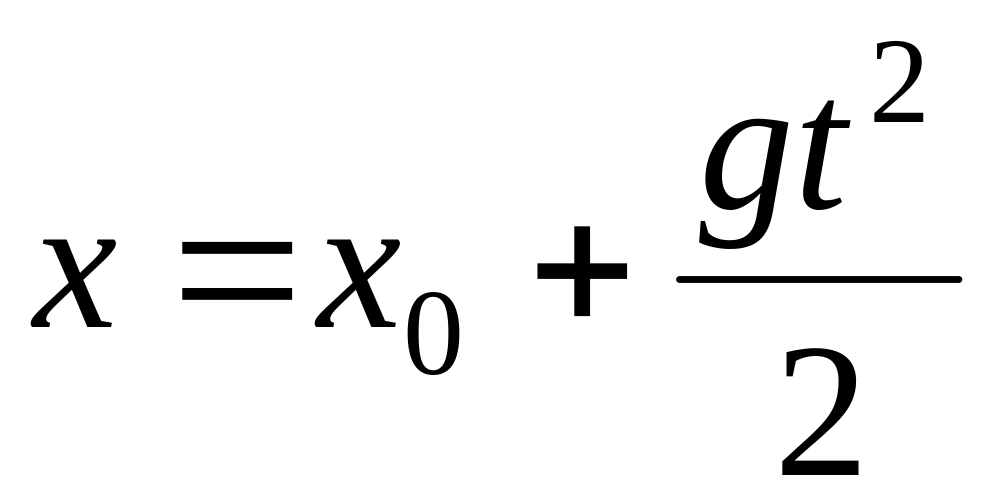
6. Уравнения движения под действием силы тяжести (ось Оу направлена вверх из точки бросания):

3. Равномерное движение по окружности. Период и частота. Линейная и угловая скорости. Центростремительное ускорение.

   1. Криволинейное движение.

М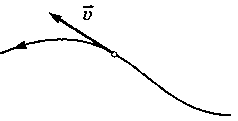 гновенная скорость при криволинейном дви­жении направлена по касательной к траектории в каждой ее точке.

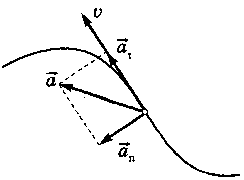
Если телу сообщить ускорение , направленное под углом к его скорости, то вектор ускоре­ния будет иметь две составляющие: касательное или тангенциальное (определяет из­менение скорости по величине) ускорение , направленное по касательной к траектории (коллинеарно векто­ру скорости), и нормальное (определяет измене­ние скорости по направлению) ускорение , направ­ленное перпендикулярно (нормально) к вектору скорости:

Е сли разбить криволинейную траекторию на до­статочно маленькие участки, то каждый участок можно рассматривать как дугу окружности соот­ветствующего радиуса. Тогда нормальное уско­рение направлено к центру этой окружности и поэтому называется центростремительным :

2. Равномерное движение по окружности.

Движение по окружности является примером криволинейного движения.

Р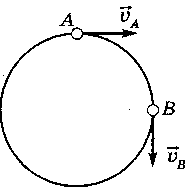 авномерное движение по окружности харак­теризуется угловой скоростью ω, линейной скоро­стью V, периодом Т, частотой .

Скорость V направлена по касательной к ок­ружности.

Линейная скорость равна модулю мгновенной скорости.

При движении материальной точки по ок­ружности модуль ее мгновенной скорости с тече­нием времени не изменяется: V = const (V _A= V _B).

Угловая скорость – в.ф.в.х. угол поворота в единицу времени.

Модуль угловой скорости численно равен отношению угла поворота подвижного радиуса ко времени поворота. Угловая скорость направлена вдоль оси, вокруг которой вращается тело, в сторону, определяемую правилом правого винта (рис. 1), и представляет собой псевдовектор . В СИ:

Период – с.ф.в.х. время одного полного оборота. ; В СИ: .

Частота – с.ф.в.х. количество оборотов единицу времени. ;

В СИ:

Отдельные точки вращающегося тела имеют различные линейные скорости, скорость каждой из точек непрерывно изменяет свое направление. Модуль линейной скорости определяется скоростью вращения и расстоянием рассматриваемой точки от оси вращения.

Центростремительное ускорение при равномерном движении по окружности зависит от харакрера движения:

1. точки А и В лежат на общем подвижном радиусе, тогда их угловая скорость ω одинакова и центростремительное ускорение выражается формулой ;

2. точки А и В связаны ременной передачей, тогда их линейная скорость V одинакова и центростремительное ускорение выражается формулой .
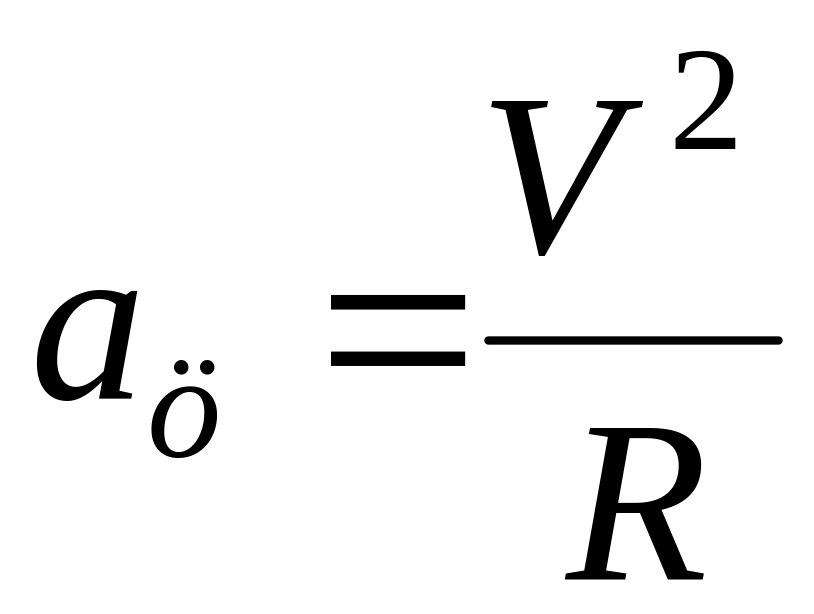