Тема 5: Основные теоремы о непрерывных и дифференцируемых функциях.

1)Определения.

1.1 ограниченная на заданном множестве функция?

1.2 точная верхняя и нижняя грань функции на заданном множестве?

1.3 Пусть заданная функция у = f(x) определена в некоторой окрестности точки а и существует такая окрестность этой точки, что для любых значений аргумента х1 и х2 из этой окрестности, таких что х1< a < x2, верны неравенства f(x1) < f(a) < f(x2). Тогда функция называется возрастающей в точке а.

Пусть функция у = f(x) определена в некоторой окрестности точки а. Тогда функция называется убывающей в точке а, если существует такая окрестность этой точки, что для любых точек х1 и х2 из этой окрестности, таких что x1< a < x2, выполнены неравенства f(x1) > f(a) > f(x2).

2)Основные теоремы и формулы.

2.1 Теорема о локальной ограниченности непрерывной функции: Если f(x) непрерывна в точке a, то существует окрестность точки a, в которой f(x) ограничена.

2.2 Теорема об устойчивости знака непрерывной функции: Пусть функция u=f(M) непрерывна в т.А и f(A)  0, тогда существует такая  -окрестность т.А, в которой f(M) имеет тот же знак, что и f(A).

2.3 Первая теорема Вейерштрасса: Если функция непрерывна на сегменте, то она ограничена на нем.

2.4 Вторая теорема Вейерштрасса: Если функция непрерывна на сегменте, то она достигает на нем своих граней (т.е. непрерывная на сегменте функция принимает свое наибольшее и наименьшее значения).

2.5 Если вещественная функция непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.

2.6 Теорема Лагранжа о среднем значении утверждает, что если функция f непрерывна на отрезке [a;b] и дифференцируема в интервале (a;b), то найдётся такая точка , что .

2.7 достаточное условие не возрастания и не убывания дифференцируемой функции на отрезке?

2.8 Если дифференцируемая функция y=f(x) возрастает на [a, b], то ее производная неотрицательна на этом отрезке, f '(x)≥ 0.

Если f(x) убывает на [a,b], то на этом отрезке. Если на (a; b), то f(x) убывает на [a, b],в предположении, что f(x) непрерывна на [a, b].

2.9 теорема о формуле коши?

2.10 Если и , то ;

Если и , то аналогично .

2.11 Формула Тейлора с остаточным членом в форме Пеано:

при

2.12 Формула Тейлора с остаточным членом в форме Лагранжа: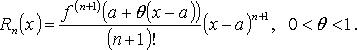

2.13

Тема 6: Исследование поведения функций и построение их графиков.

1)Определения.

1.1 Говорят, что функция f(x) имеет в точке c локальный максимум (минимум), если найдётся такая окрестность точки c, в пределах которой значение f(C) является наибольшим (наименьшим) среди всех значений функции в этой окрестности, то есть всюду в этой окрестности выполняется условие (  ).

1.2 Направление выпуклости графика функции: Говорят, что график функции f(x) имеет на интервале (a:b) выпуклость, направленную вниз (вверх), если график этой функции в пределах данного интервала лежит выше (ниже) любой своей касательной.

1.3 Точка M(x₀ ,f (x₀ )) графика функции y=f(x) называется точкой перегиба этого графика, если существует такая окрестность точки x₀ оси абсцисс, в пределах которой график функции y=f(x) слева и справа от точки x₀ имеет разные направления выпуклости.

1.4 Наклонные -  это такая асимптота, уравнение которой является уравнением прямой линии

, при существовании пределов , .

1.5 Вертикальная асимптота — прямая вида x=a при условии существования предела .