2.9 Давление Жидкости на горизонтальное дно сосуда

Согласно формуле (2.23) сила давления жидкости на горизонтальное дно сосуда равна весу жидкости в объеме цилиндра с основанием равным площади дна, и высотой, равной глубине этого сосуда.

На рисунке представлены 3 различных сосуда по форме, однако, с равными площадями дна.

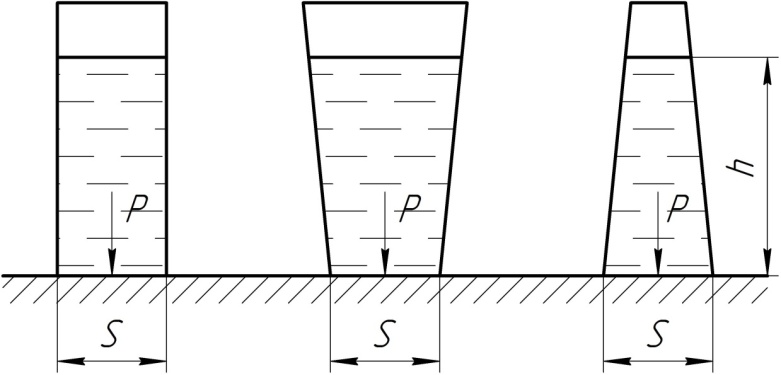
Поэтому, несмотря на разную. Форму сосудов, давление жидкости на дно будет одинаковым во всех трех случаях.

2.10 Равновесие несмешивающихся жидкостей

Поверхность уровня – это поверхность все точки которой имеют одинаковое значение рассматриваемой функции (температура, потенциал)

Поверхность равного давления будем называть поверхностью уровня.

Свойства поверхности:

1. Две поверхности уровня не пресекаются. Т.к p₁<>p₂

2. Внешние объемные силы направлены нормально к поверхности уровня.

3. Поверхность уровня есть горизонтальная поверхность.

Предположим, что две несмешивающиеся между собой жид­кости с различной плотностью помещены в одном и том же ре­зервуаре и находятся в равновесии. В таком случае и поверхностьих раздела будет также неподвижна. Определим вид такой по­верхности. Свободная поверхность является поверхностью уров­ня (во всех ее точках давление равно р₀),т. е. представляет собой горизонтальную плоскость.

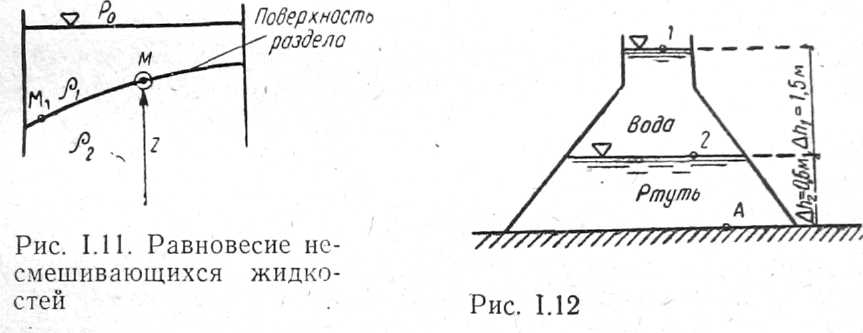
Рассмотрим условия равновесия на неподвижной поверхно­сти раздела жидкостей с плотностями ρ1 и ρ2. Предположим, что поверхность раздела занимает положение, как показано на рис. 1.11.

Напишем основное дифференциальное уравнение для жид­кости: с плотностью

и с плотностью

Возьмем на поверхности раздела две точки (точки МиМ₁на рис. 1.11). При переходе от одной точки к другой давление рменяется на величину dpи поэтому в указанных выше равенст­вах dpбудет одним и тем же по величине.

Тогда:

или

Так как g≠0то, если p1 ≠ p2, то dz=0и, следовательно, для поверхности раздела справедливо z=const, т. е. поверх­ность раздела в этом случае может быть только горизонтальной, Тот же результат был бы получен и при рассмотрении условий равновесия на поверхностях раздела других жидко­стей, находящихся в резервуаре.

Итак, приходим к общему заключе­нию, что при равновесии несмешивающихся жидкостей поверхности их разде­ла будут горизонтальными плоскостями.

Жидкости при этом расположатся по высоте (считая сверху вниз) в порядке воз­растания их плотностей, что следует не­посредственно из общих условий устой­чивого равновесия механической систе­мы в поле тяготения: центр тяжести системы расположенные в наиболее низкой точке, или, иначе, потенциальная энергия системы должна быть минимальной.

2.11 Относительное равновесие

Относительным равновесием жидкости называется такой случай ее движения, при котором отдельные ее частицы не сме­щаются одна относительно другой и вся масса жидкости дви­жется как твердое тело. Например, вообразим, что некоторый замкнутый резервуар (наполненный жидкостью) движется с по­стоянной скоростью (или постоянным ускорением) в любом на­правлении и с этой же скоростью (или ускорением) движется также и каждая частица жидкости, находящейся в резервуаре. Очевидно, что рассматриваемая масса жидкости будет неподвиж­на в координатной системе, связанной с движущимся резервуа­ром. Такое движение жидкости представляет собой относитель­ное ее равновесие.

Рассмотрим два практически наиболее интересных случая: движение по вертикали и вращательное движение относительно вертикальной оси.

1. Движение по вертикали

Допустим, что открытый резервуар вместе с находящейся в ней жидкостью движется в вертикальном направлении сверху вниз с некоторым постоянным ускорением j, меньшим ускорения свободного падения g или равным ему (рис. 1.14).

Определим вид поверхности уровня и закон распределения гидростатического давления. Заметим предварительно, что, со­гласно принципу даламбера, при любом движении тела можно пользоваться уравнениями статики, если к системе действую­щих сил прибавить силы инерции (они направлены в сторону, противоположную направлению движения). Такая система сил будет уравновешена, и тело можно считать находящимся в рав­новесном состоянии.

Следовательно, мы можем воспользоваться уравнением поверхности уровня:

рис. 1.14

Чтобы написать уравнение поверхности уровня для данного случая, определим X, Y и Z. Ускорениями действующих сил бу­дут ускорения свободного падения g (9,81 м/с²) и ускорение сил инерции j_и. Оба ускорения направлены параллельно оси Oz. Сле­довательно, проекции этих ускорений на оси хну равны нулю: Х=0 и Y=0, а

Итак, уравнение поверхности уровня в дифференциальной форме примет следующий вид:

Если

Интегрируя, находим z = const. А это значит, что - поверх­ность уровня будет горизонтальной плоскостью.

Если j=g,

то =1 и тогда dz может быть и не равным нулю, следовательно, форма свободной поверхности может быть произвольной.

То есть при падении с ускорением g (свободное падение) жидкость в невесомости, значит форма поверхности произвольная.

Определим закон распределения Гидростатического давления.

В условиях спуска по вертикали с ускорени­ем j закон распределения гидростатического давления будет та­ким же, как и в обычных условиях равновесия жидкости в поле земного тяготения, р = p_о + γ^,h но с тем отличием, что в подвижной системе координат удельный вес меньше, причем, если j=g, т. е. при свободном падении, объемный вес γ'=0. Жидкость стала «не­весомой».

)

2. Статическое вращение жидкости

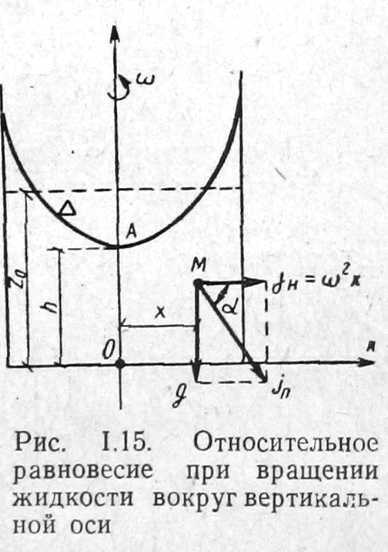
Предположим, что ци­линдр с водой, налитой до глубины zо, приведен во вращатель­ное движение вокруг вертикальной оси Oz с угловой скоростью ω, с-1 (рис. 2.15).

Вращающиеся стенки цилиндра приведут во вращательное движение ближайшие к стенкам слои жидкости, а затем, вслед­ствие вязкости жидкости — и всю ее массу. По истечении извест­ного времени все частицы жидкости будут вращаться примерно с одной и той же угловой скоростью ω.Допустим, что такой момент времени наступил.

Определим форму поверхности уровня и, в частности, свободной поверх­ности.Как и в первой задаче, будем исходить из общего дифферен­циального уравнения поверхности уровня

Так как движение симметрично относительно оси вращения, то рассмотрим равновесие частиц жидкости, расположенных в плоскости координат xOz, вращающейся с угловой скоростью ω. Как и в предыдущей задаче, объемными силами будут силы земного тяготения и силы инерции. Последняя представляет собой центробежную силу, направленную параллельно оси Ох и в сторону от оси вращения.

В точке М на расстоянии х от оси Oz линейная скорость ча­стицы u=хω, поэтому для нее центробежное ускорение

и следовательно полное ускорение внешних объемных сил:

Очевидно, что в данном случае:

Делая подстановку получим:

или

и после интегрирования

что представляет собой уравнение параболы с вершиной на оси Oz в точкеА, имеющей координату z_i=h.

Поскольку уравнение симметрично относительно оси Oz, то поверхность уровня будет представлять собой парабо­лоид вращения.

Запишем закон распределения давления:

р_абс=р_атм+p_изб

В качестве примеров можно решить задачи 1.2, и 1.3 на странице 50

Уч. Альтшуль – Гидравлика и Аэродинамика.