9.10 Истечение жидкости и газа через отверстия и насадки.

СТРУЯ - форма течения жидкости, при к-рой жидкость (газ) течёт в окружающем пространстве, заполненном жидкостью (газом) с отличающимися от струи параметрами (скоростью, темп-рой, плотностью, составом и т. п.).

В приближённой модели течения идеальной жидкости граница струи является поверхностью тангенциального разрыва и вещество струи не смешивается с веществом окружающего пространства.

В реальных течениях ввиду неустойчивости тангенциального разрыва между струей и окружающим её внешним пространством возникает слой вязкого перемешивания, в к-ром все рассмотренные параметры течения изменяются непрерывно от соответствующих струи до соответствующих внеш. пространству.

Струйные течения классифицируют по наиб. существ. признакам.

1. Струи, вытекающие из сопла или отверстия в стенке сосуда. В зависимости от формы поперечного сечения отверстия (сопла) могут быть:

- круглые, квадратные, плоские.

в зависимости от направления скорости течения на срезе сопла различают:

- осевые, веерные и закрученные С.

2. В соответствии с характеристиками веществ рассматривают струи:

- капельной жидкости, газа, плазмы.

В особый класс выделяются

- двухфазные струи,( напр. газовые, содержащие жидкие или твёрдые частицы, или С. жидкости, заполненные пузырьками газа.)

Для сжимаемых газов в зависимости от значения М различают:

-дозвуковые ( М<1) и сверхзвуковые ( М>1). Аналогичная классификация в зависимости от числа М проводится и для скорости среды, в к-рую вытекает С.

3) В зависимости от направления скорости течения газа (жидкости) в окружающей среде различают:

- вытекающие в спутный (направленный в ту же сторону), встречный и сносящий потоки (напр., С. жидкости, вытекающая из трубы в реку и направленная соответственно по течению, против течения и под углом к скорости течения реки).

3. По составу жидкости (газа) в струе и окружающей её неподвижной среды

- Струя наз. затопленной – составы идентичны (напр., С. воздуха, вытекающая в неподвижную атмосферу).

-С. наз. свободной, если она вытекает в среду, не имеющую ограничивающих поверхностей,

-п о л у о г р а н и ч е н н о й, если она течёт вдоль плоской стенки,

- с т е с н ё н н о й, если вытекает в среду, ограниченную твёрдыми стенками (напр., С., вытекающая в трубу большего диаметра, чем диаметр сопла).

4. В соответствии с физ. особенностями веществ струи и внеш. среды различают:

- струи смешивающиеся (С. газа, вытекающая в воздух)

- несмешивающиеся (С. воды, вытекающая в атмосферу). Поверхность несмешивающейся С. неустойчива, и на нек-ром расстоянии от среза сопла С. распадается на капли. Дальнобойность такой Струи - расстояние, на к-ром она сохраняется монолитной,(- зависит от физ. свойств её вещества, кинётич. энергии и уровня начальных возмущений в сопле.)

В случае, когда вещество С. способно смешиваться с веществом внеш. среды, на её поверхности образуется область вязкого перемешивания - струйный пограничный слой. В зависимости от режима течения в этом слое различают С. ламинарные и турбулентные. (Так, струя, вытекающая из сопла реактивного двигателя летящего самолёта,- пример турбулентной сверхзвуковой С., вытекающей в спутный поток, к-рый в зависимости от скорости полёта самолёта может быть дозвуковым или сверхзвуковым.)

В д о з в у к о в о й турбулентной струе статическое давление в любой точке струи почти постоянно и близко к давлению в окружающем пространстве. Такие С., называемые и з о б а р и ч е с к и м и, широко распространены.

Рис. 1. Спутная изобарическая струя газа: b_с - радиус сопла; b - радиус струи; α-угол наклона внутренней границы начального участка; θ - угол расширения внешней границы струи.

На срезе сопла спутной изобарической С. (сечение аа, рис. 1) скорость течения V_c отличается от скорости спутного потока V_a.

На границе струи и внеш. потока образуется слой вязкого перемешивания В, состоящий из газа струи и смешивающегося с ней газа внеш. среды.

Расход газа в струе, ограниченной размером b, по мере удаления от среза сопла монотонно увеличивается за счёт подсасываемого из внеш. пространства газа, но суммарное количество движения, определённое по избыточной скорости, остаётся неизменным.

В нач. участке струи при х<х_н расширяющийся слой перемешивания ещё не достигает оси течения; скорость V_c вблизи оси постоянна и равна скорости на срезе сопла. В переходном участке С. ( х _н<х<х _н + х _п ) вязкое перемешивание распространяется на весь объём струи, скорость течения на оси уменьшается, но профили скоростей ещё продолжают изменяться.

В осн. участке струи ( х>х _н + х _п ) скорость течения на оси уменьшается, профили относит, скорости ΔV/ΔV_m=f(y/b )становятся неизменными (автомодельными) ΔV =V_y -V_a, ΔV_m=V_m-V_a - избыточные скорости в рассматриваемой точке течения на расстоянии у от оси струи и на оси).

Аналогично профилю скорости ведут себя профили избыточных температуры и концентрации в осн. участке струи; все они связаны зависимостью:

где ΔT=T-T_а, ΔТ_m=Т_m -Т_а, Δχ= χ- χ_a, Δχ_m= χ_m- χ_a - соответствующие значения избыточных темп-ры Т и концентрации , Рr - число Прандтля, для осесимметричных газовых струй Pr = 0,75-0,8.

Углы расширения границ слоя перемешивания струи α и θ различны для полей скорости, темп-ры и концентрации.

Для турбулентных струй сжимаемого газа углы α и θ тем больше, чем больше отличается от 1 спутность потока m =V_a/V_c, Кроме того, углы α и θ, существенно увеличиваются при увеличении ср. значения турбулентности потока , где - величина поперечной пульсации скорости, а - средняя величина скорости в струе.

Таким образом, течение в изобарич. турбулентной спутной струе. в осн. определяется безразмерными числами Маха, Прандтля, спутности течения m, и турбулентности течения

Схема течения в изобарической, с в е р х з в у к о в о й спутной струи такая же, как для дозвуковой (рис. 1).

Скорость течения на оси изобарической струи постоянна в пределах начального (изоэнтропического) участка течения х<=х_н, а в дальнейшем монотонно изменяется, стремясь к значению скорости в окружающем пространстве.

В осн. участке затопленной струи х>х_н+х_п скорость на оси изменяется по закону для осесимметричных сртуй и по закону для плоских ( -безразмерное расстояние от среза сопла).

Независимо от формы поперечного сечения струи на срезе сопла, начиная с нек-рого расстояния , в осн. участке струя. становится круглой.

В случае, когда давление Р_с в сверхзвуковой струе на срезе сопла отличается от давления Р_а в окружающей атмосфере (p_c>p_а) Струя наз. нерасчётной и к числу параметров, характеризующих течение в С., добавляется нерасчётность истечения n =р_с/р_а, определяющая картину ударных волн в струе. и во внеш. пространстве.

Примером такого течения является С., вытекающая из сопла вертикально стартующей ракеты. Для неё условие n=1 будет иметь место только в одной точке траектории.

Расчетный нерасчетные режимы иситечения из сопла:

Расчетный если P_c=P_a

Не равно значит нерасчетный –

P_a>P_c недорасширение

P_a<P_c перерасширение.

Рис. 2. Сверхзвуковая нерасчётная струя в сверхзвуковом спутном потоке.

Осесимметричная нерасчётная струя. (рис. 2), вышедшая из сечения а-а сопла расширяется в веере волн разрежения, к-рые отражаются от границы струи в форме волн сжатия, огибающей к-рых является "висячая" ударная волна 1.

Осесимметричная волна 1 отражается вблизи оси в области 3, причём в зависимости от режима течения, определяемого нерасчётностью n и отношением чисел М_с/М_а , отражение может быть простым или "маховским", когда вблизи оси течения имеет место прямая ударная волна, за к-рой скорость газа становится дозвуковой.

Отражённые ударные волны 2 пересекают внеш. границу течения, при этом возникают ударные волны 4 во внеш. сверхзвуковом потоке и отражённая волна внутри С. (на рис. 2 не показана).

Начальный газодинамич. участок струи х_нг от среза сопла до сечения, в к-ром отражённая ударная волна пересекает границу струи, наз. первой "бочкой".

Вязкий слой перемешивания В, постепенно нарастая, достигает оси течения на расстоянии x_нв, которое наз. начальным участком вязкого течения. Далее следуют участки переходного х_n и осн. x_o течений, в к-рых условия течения близки к соответствующим течению в осн. участке изобарич. Струи.

В спутном потоке, обтекающем нач. участок струи, возникает ударная волна 5 и давление на внешней поверхности первой "бочки" становится монотонно убывающим.

В реальной нерасчётной струе. (рис. 3) в результате отражения ударных волн наблюдается неск. "бочек", к-рые заполняют всю длину невязкого течения вблизи оси С. на участке x_нв, а иногда выходят за её пределы.

В большинстве расчётных методик обычно рассматривают только первую "бочку", поскольку она содержит наиб. интенсивные ударные волны, а дальнейшее течение считают изобарическим.

Рис. 3. Теневая фотография осесимметричной сверхзвуковой нерасчётной затопленной струи: 1- висячая ударная волна; 2- отражённые ударные волны; 3 - область отражения ударных волн.

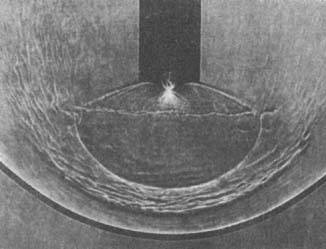
Рис. 5. Теневая фотография сверхзвуковой струи, вытекающей во встречный поток.

Информация о распределении скорости, темп-ры, концентрации компонентов в сечениях С., расположенных на 'выбранном расстоянии от среза сопла, необходима для определения силовых и тепловых нагрузок на стартовые сооружения и элементы конструкций ракетных и самолётных комплексов, на лопатки газовых турбин и др.

121