
- •Основные понятия и определения
- •1.1 Плотность
- •1.2. Вязкость
- •1.3 Модели жидкой среды
- •1.4 Ньютоновские и Аномальные жидкости
- •1.5Силы действующие в жидкости
- •1.5.1 Массовые силы
- •1.5.2 Поверхностные силы
- •1.5.3 Тензор напряжения
- •1.5.4 Касательные напряжения
- •1.6 Обобщенная Гипотеза Ньютона
- •2. Гидростатика
- •2.1 Равновесное состояние
- •2.2 Гидростатическое давление в точке
- •2.3 Общие Дифференциальные уравнения равновесия жидкости
- •2.4 Основное уравнение гидростатики в дифференциальной форме
- •2.5 Основное уравнение гидростатики в интегральной форме для несжимаемой жидкости
- •2.6 Гидростатический напор
- •2.7 Определение силы давления жидкости на поверхности тел
- •2.8 Плоская поверхность
- •2.9 Давление Жидкости на горизонтальное дно сосуда
- •2.10 Равновесие несмешивающихся жидкостей
- •2.11 Относительное равновесие
- •2.12 Равновесие Газов
- •2.13 Международная стандартная атмосфера
- •3 Основные уравнения Гидро Газодинамики
- •3.1Основные понятия и определения движения жидкости
- •3.2 Уравнение Бернулли для элементарной струйки несжимаемой жидкости
- •3.3 Два метода исследования движения жидкости Лагранжа и Эйлера
- •3.4 Уравнение линии тока
- •3.5 Уравнение неразрывности
- •3.6 Вихревое и безвихревое движение жидкости
- •3.7 Интегрирование уравнений Эйлера для потенциального потока в случае установившегося движения
- •3.8 Уравнения Навье Стокса
- •4 Режимы течения.
- •4.1 Режимы течения
- •4.2 Число Рейнольдса
- •4.3 Виды гидравлических сопротивлений
- •4.2 Общая формула для потерь напора на трение при равномерном движении жидкости в трубах
- •4.4 Особенности ламинарного и турбулентного движения жидкости в трубах
- •4.5 Ламинарное равномерное движение жидкости
- •4.6.Турбулентное равномерное движение жидкости в трубах
- •4.7 Касательное напряжение при турбулентном движении
- •4.8 Полуэмпирические теории турбулентности
- •4.9 Начальный участок турбулентного движения
- •5. Потери в потоке
- •5.1 Потери напора на трение в круглой трубе
- •5.2 Опытные данные о распределении скоростей и потерях напора
- •5.3 Эмпирические формулы для коэффициента гидравлического трения
- •5.4 Движение жидкости в трубах некругового сечения
- •5.5 Снижение потерь напора на трение при турбулентном движении
- •5.6 Местные гидравлические сопротивления
- •5.6.1 Внезапное расширение трубопровода
- •5.6.2 Внезапное сужение трубопровода
- •5.6.3.Вход в трубу через диафрагму
- •5.6.4.Резкое уменьшение диаметра трубы
- •5.6.5 Постепенное расширение
- •5.6.6 Постепенное сужение трубы
- •6.1 Циркуляция скорости
- •6.2 Степенные законы распределения скоростей
- •6.3 Модели турбулентности
- •7. Основы теории пограничного слоя
- •7.1 Понятие о пограничном слое
- •7.2 Ламинарный погранслой
- •7.3 Турбулентный погранслой
- •7.4 Отрыв пограничного слоя, и отрыв потока
- •7.4 Методы управления пограничным слоем
- •7.4.1 Предотвращение отрыва слоя при помощи сосредоточенного отсоса из него жидкости или ввода в слой жидкости.
- •7.4.2 Затягивание ламинарного участка слоя путем придания носовой части тела оптимальной формы
- •7.4.3 Ламинаризация пограничного слоя при непрерывном (распределенном) отборе потока
- •7.4.4 Ламинаризация пограничного слоя при щелевом отборе
- •8 Газодинамические процессы {Модуль 3}
- •8.1 Уравнения течения жидкости в трубах переменного сечения
- •8.2 Уравнение неразрывности струи
- •8.3 Сопло Лаваля и скорость истечения
- •8.4 Скорость звука
- •8.5 Газодинамические функции
- •8.5.1 Гдф характеризующие термодинамическое состояние.
- •8.5.2 Гдф характеризующие Разгон потока (q, y, ξ)
- •8.5.3 Гдф z, f, r – характеризуют импульс потока.
- •9 Плоский сверхзвуковой поток
- •9.1 Термодинамика ударных волн
- •9.2 Происхождение ударных волн
- •9.3 Ударная волна, вызванная летательным аппаратом
- •9.4 Скачки уплотнения. Образование скачков уплотнения
- •9.4.1. Прямой скачок
- •9.4.2 Косые скачки уплотнения
- •9.5 Формы скачков уплотнения
- •9.6 Критическая скорость
- •9.7 Течение Прандтля Майера
- •9.8 Закон обращения воздействия
- •1) Расходное воздействие на газовый поток.
- •2) Механическое воздействие.
- •3) Тепловое воздействие
- •4) Воздействие трением.
- •9.9 Гидравлический удар
- •9.10 Истечение жидкости и газа через отверстия и насадки.
7.2 Ламинарный погранслой
В начальной части П.С. течение является ламинарным, упорядоченным. Отдельные частицы жидкости движутся по плавным траекториям, не пересекаясь и не перемешиваясь друг с другом. Форма этих траекторий близка к форме обтекаемого тела.
В случае стационарного двумерного течения эти упрощённые уравнения Навье-Стокса, известные как уpавнения П.С., или уравнения Прандтля, представляют собой нелинейные днфференциальные ypавнения параболического типа и имеют вид:
уравнение сохранения количества движения
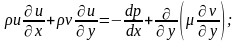 (1)
(1)
уравнение сохранения энергии
 (2)
(2)
уравнение неразрывности
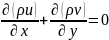 (3)
(3)
Здесь: х
и y - координаты,
направленные вдоль поверхности тела и
по нормали к ней, u и
v - составляющие
скорости вдоль этих координат,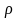 - плотность, р
- давление,
- плотность, р
- давление,
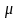 - коэффициент динамической вязкости, Т
- температура,
- коэффициент динамической вязкости, Т
- температура,
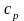 - удельная теплоёмкость при постоянном
давлении,
- удельная теплоёмкость при постоянном
давлении,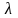 - коэффициент теплопроводности.
- коэффициент теплопроводности.
Граничные условия к системе уравнений (1) - (3) имеют вид:
при y = 0 величины
u = 0, v
=
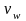 ,
Т =
,
Т =
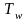 ;
;
при y и y
и y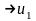 величина Т
величина Т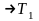 ;
;
Для решения уравнений П.С. используются различные методы, среди которых можно выделить две основные группы - численные (конечно-разностные) и интегральные.
Первая группа методов основана на численном интегрировании исходных уравнений П.С. методом сеток, или конечных разностей.
Вторая группа методов основана на использовании уравнений П.С. в интегральной форме. В этих уравнениях в качестве зависимых переменных выступают некоторые интегральные характеристики П.С.:
Толщина ламинарного погран слоя:

Где х- расстояние от передней кромки (от начала обтекания)
толщина вытеснения
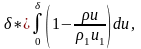 (6)
(6)
толщина потери импульса
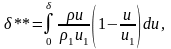 (7)
(7)
толщина потери энергии
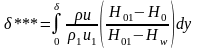 (8)
(8)
(индексы "1" относятся к внешнему потоку, "01" - к границе П.С., "0" - к П.С., а "w" - к обтекаемой поверхности). Интегральные уравнения П.С. получаются из дифференциальных уравнений типа (1) - (5) интегрированием последних по поперечной координате от 0 до внешней границы П.С.
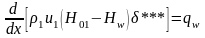 (10)
(10)
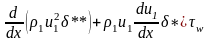 (9)
(9)
Где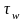 - напряжение трения на поверхности тела,
а
- напряжение трения на поверхности тела,
а - тепловой поток через его поверхность.
Интегральные уравнения позволяют учесть
изменяющиеся условия течения вверх по
потоку от рассматриваемой точки тела.
Для решения интегральных уравнений
П.С. (9) - (10) необходимо иметь сведения о
профилях скорости и энтальпии (или
температуры) внутри П.С.
- тепловой поток через его поверхность.
Интегральные уравнения позволяют учесть
изменяющиеся условия течения вверх по
потоку от рассматриваемой точки тела.
Для решения интегральных уравнений
П.С. (9) - (10) необходимо иметь сведения о
профилях скорости и энтальпии (или
температуры) внутри П.С.
7.3 Турбулентный погранслой
По мере увеличения расстояния вдоль поверхности тела местное число Рейнольдса возрастает и начинает проявляться неустойчивость ламинарного течения по отношению к малым возмущениям. Такими возмущениями могут служить пульсации скорости во внешнем набегающем потоке, шероховатость поверхности и другие факторы.
В результате ламинарная форма течения переходит в турбулентную, при этом на главное "осреднённое" движение жидкости или газа в продольном направлении накладываются хаотические пульсации движения в поперечном направлении, происходит интенсивное перемешивание жидкости, вследствие чего интенсивность переноса в поперечном направлении кол-ва движения, теплоты и массы резко увеличиваются.
Толщина турбулентного пограничного слоя:

Потеря устойчивости и переход
к турбулентному режиму течения внутри
П.С. происходят при некотором характерном
числе Рейнольдса, которое называется
критическим. Величина
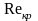 зависит от множества факторов - степени
турбулентности набегающего потока,
шероховатости поверхности,числа Маха
М внешнего потока, относительной
температуры поверхности, вдува или
отсоса вещества через поверхность тела
и других.
зависит от множества факторов - степени
турбулентности набегающего потока,
шероховатости поверхности,числа Маха
М внешнего потока, относительной
температуры поверхности, вдува или
отсоса вещества через поверхность тела
и других.
Переход ламинарного режима течения в турбулентный связан с потерей устойчивости, то сам этот процесс не является достаточно стабильным, вследствие чего имеет место областью перехода.
Изменение режима течения в П.С. сопровождается утолщением слоя и деформацией профилей скорости, температуры и концентраций. Одновременно возрастают коэффициент поверхностного трения, тепло- и массообмена, а также изменяется характер их распределения вдоль поверхности тела (рис. 4).
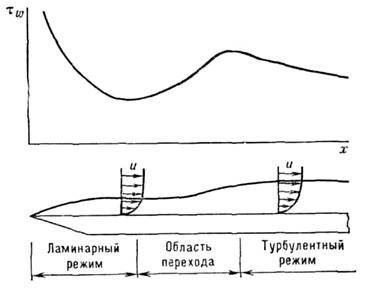
Рис. 4. Изменение режима течения в пограничном слое и поверхностного трения на плоской пластине
Течение внутри турбулентного
П.С. носит пульсационный, хаотический
характер: В этом случае при матемематическом
описании течения каждый параметр можно
представить в виде суммы осреднённого
по времени, или среднего, значения и
пульсационного. Например,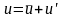 ,
,
 .
Интеграл по времени от пульсац.
составляющей любого параметра за
достаточно большой интервал времени
.
Интеграл по времени от пульсац.
составляющей любого параметра за
достаточно большой интервал времени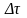 (строго говоря, при
(строго говоря, при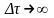 )
равен нулю
)
равен нулю
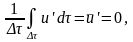

Прандтлем предожена гипотеза
"пути перемешивания" l,
позволяющая выразить коэффициент
турбулентной вязкости через среднюю
плотность и градиент средней скорости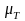 :
:
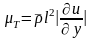 (11)
(11)
В общем случае турбулентный П.С. можно по высоте разделить на 3 области (рис. 5):
пристеночный ламинарный подслой, где турбулентные пульсации затухают и решающую роль играют молекулярные вязкость и теплопроводность
турбулентное ядро, в котором турбулентные вязкость и теплопроводность существенно превышают соответствующие молекулярные переносные свойства
промежуточная переходная область.
Распределение скорости внутри турбулентного ядра описывается некоторым универсальным эмпирическим законом:
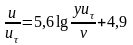
Где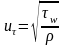 - так называемая скорость сдвига, или
динамич. скорость, а
- так называемая скорость сдвига, или
динамич. скорость, а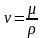 - кинематическая вязкость.
- кинематическая вязкость.
При построении приближённых методов расчёта турбулентного П.С. широко используются также степенные профили скорости и температуры:
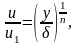
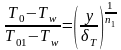
Где
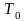 ,
,
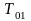 и
-
соответствующие температуры торможения
в П.С., на границе П.С. и стенки. Значения
показателей степени для дозвуковых
скоростей изменяются от 1/7 до 1/9 при
увеличении числа Рейнольдса, и
несущественно возрастают при больших
числах Маха.
и
-
соответствующие температуры торможения
в П.С., на границе П.С. и стенки. Значения
показателей степени для дозвуковых
скоростей изменяются от 1/7 до 1/9 при
увеличении числа Рейнольдса, и
несущественно возрастают при больших
числах Маха.
Экспериментальная формула коэффициента трения:
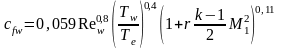
Где - коэф. поверхностного трения,
- коэф. поверхностного трения,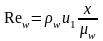 - число Рейнольдса,
- число Рейнольдса,
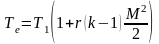 - равновесная темп-pa
стенки, r - коэффициент
восстановления температуры,
- равновесная темп-pa
стенки, r - коэффициент
восстановления температуры,
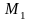 - число Маха внешнего потока,
- число Маха внешнего потока,
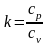 -
отношение теплоёмкостей при постоянном
давлении и постоянном объёме.
-
отношение теплоёмкостей при постоянном
давлении и постоянном объёме.
Из аналогии процессов тепломассообмена и трения позволяет для безразмерного коэффициента теплообмена на пластине - числа нусельта Nu - записать формулу, которая хорошо согласуется с имеющимися экспериментальными данными:
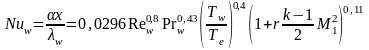
( -
коэф. теплоотдачи,
-
коэф. теплоотдачи,
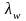 - коэф. теплопроводности газа на стенке).
Для переноса этой зависимости на случай
П.С. на теле произвольной формы может
быть использован предложенный метод
"эффективной длины", предполагающий,
что тепловой поток в рассматриваемой
точке тела будет таким же, как в некоторой
точке на пластине при одинаковых местных
параметрах течения и при условии, что
в рассматриваемых точках тела и пластины
толщины потери энергии
- коэф. теплопроводности газа на стенке).
Для переноса этой зависимости на случай
П.С. на теле произвольной формы может
быть использован предложенный метод
"эффективной длины", предполагающий,
что тепловой поток в рассматриваемой
точке тела будет таким же, как в некоторой
точке на пластине при одинаковых местных
параметрах течения и при условии, что
в рассматриваемых точках тела и пластины
толщины потери энергии (8) также одинаковы.
(8) также одинаковы.

Рис. 5. Внутреннее строение турбулентного пограничного слоя.
Течение в П.С. оказывает решающее влияние на явление отрыва потока от поверхности обтекаемого тела как во внешних (например, обтекание крыла), так и во внутренних (например, течение в диффузоре) течениях.
