1. Геометрические векторы. Основные определения

В математике, физике, теоретической механике приходится иметь дело с величинами двух типов: одни имеют чисто числовой характер; другие же имеют не только числовую характеристику, но и связаны с понятием о направлении в пространстве. Рассмотрим, например, температуру, массу, энергию, скорость, ускорение, силу. Отличие последних трех величин от первых трех состоит в том, что с ними должно быть связано понятие о направлении. Первые три величины, не связанные с понятием о направлении, называются скалярами. Остальные три величины, имеющие определенное направление, называются векторами.

Так, при измерении температуры, мы получим положительное или отрицательное число, характеризующее ее величину в градусах. Точно так же можно измерить массу, энергию.

Определение: Скаляр – элемент числового поля (Вещественного или Комплексного). Скаляр – другое название вещественного числа.

Определение Геометрический вектор – упорядоченная пара точек (направленный отрезок)

=

Два направленных отрезка называются равными, если они имеют одинаковые направления и одинаковые длины.

Определение Геометрический вектор – класс равных друг другу направленных отрезков.

Свойства векторов как класса:

Классы направленных векторов или векторы как класс – либо непересекаются либо совпадают.

Две линейных операции: сложение и умножение на число.

Сложение:

Суммой двух векторов и как классов называется вектор , который получается:

От фиксированной точки О откладывается (берётся представитель вектора и откладывается от точки О), далее от конца полученного отрезка откладывается вектор . Вектор - это по определению представитель с началом в точке О и в конце, совпадающим с концом вектора . =

Поскольку сумму определили с помощью представителей, то требуется доказать что сумма не зависит от выбора начальной точки.

Берем вновь фиксированную точку , далее откладываем от точки и точно так же как в первом случае от точки откладываем представитель. И вынуждены считать, что представитель так же суммы.

Теперь представители должны входить в один класс, суммы.

ДЗ: Проверка корректности! Возможны разные случаи расположения. И разные векторы.

Произведение данного вектора на данное число:

Этот вектор сонаправлен с исходным если модуль числа равен самому числу и противоположно направлен если модуль числа и само число отличаются знаком.

Чтобы умножить данный вектор на нужно взять начальную точку О, отложить если >0, то отложить отрезок , если <0, то от О отложить отрезок в противоположную сторону .

ДЗ: Проверка корректности!

Свойства линейных операций:

1) , , , .

2) |

3) | + = + =

- противоположный, =

4) = , ,

1+2+3=>группа; 1+2+3+4=> коммутативная абелева группа.

5) - распределительное

6) - распределительное

7)

8) , , ,

Числовые матрицы.

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы чисел и допускающий алгебраические операции (сложение, вычитание, умножение) между ним и другими подобными объектами. Обычно матрицы представляются двумерными (прямоугольными) таблицами. Иногда рассматривают многомерные матрицы или матрицы непрямоугольной формы. Обычно матрицу обозначают заглавной буквой латинского алфавита и выделяют круглыми скобками «(…)» (встречается также выделение квадратными скобками «[…]» или двойными прямыми линиями "||…||"). Числа, составляющие матрицу (элементы матрицы), часто обозначают той же буквой, что и саму матрицу, но строчной (к примеру a₁₁ является элементом матрицы А). У каждого элемента матрицы есть 2 нижних индекса (a_ij) — первый «i» обозначает номер строки, в которой находится элемент, а второй «j» — номер столбца. Говорят «матрица размера », подразумевая, что в матрице m строк и n столбцов. В одной матрице всегда , Если количество строк матрицы равно количеству столбцов, то такая матрица называется квадратной.

Среди прямоугольных выделяется нулевая матрица, состоящая из одних нулей

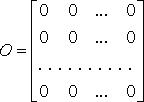
Матрицы равны, если они имеют одинаковые размеры m=m’, n=n’ и элемениты с одинаковыми адресами совпадают.

Диагонали матрицы:

Г лавная диагональ: Побочная диагональ:

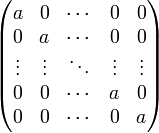Матрица называется диагональной, если вне главной диагонали все нули.

A=

Для квадратных матриц существует единичная матрица E (аналог единицы для операции умножения чисел) такая, что умножение любой матрицы на неё не влияет на результат, а именно

EA = AE = A

У единичной матрицы единицы стоят только по главной диагонали, остальные элементы равны нулю

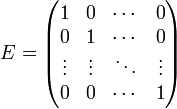
Матрицу называют симметрической, если её элементы, симметричные главной диагонали одинаковы(a_ij= a_ji)

Матрицу называют кососимметрической, или антисимметрической если её элементы относительно главной диагонали,отличаются только знаком.(a_ij= - a_ji)

Матрица называется треугольной если все ее элементы ниже главной диагонали или выше главной диагонали – нули.

Верхняя треугольная матрица Нижняя треугольная матрица

Операции над матрицами

1) Транспонирование матрицы (обозначение: A^T) — операция, при которой матрица отражается относительно главной диагонали, то есть

Если A — матрица размера , то A^T — матрица размера .

2) Умножение матрицы A на число λ (обозначение: λA)

Каждый элемент данной матрицы умножается на число (b_ij = λa_ij), размеры матрицы сохраняются.

3) Умножение матриц (обозначение: AB, реже со знаком умножения ) — есть операция вычисления матрицы C, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго.

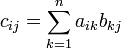
В первом множителе должно быть столько же столбцов, сколько строк во втором. Если матрица A имеет размерность , B — , то размерность их произведения AB = C есть .

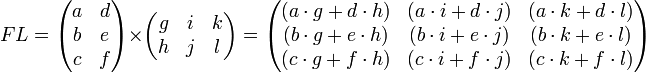
Возводить в степень можно только квадратные матрицы.

Линейные операции над матрицами и их свойства:

где m, n фиксированные – множество матриц фиксированного размера над числовым полем Р.

I свойства сложения

1) A + (B + C) = (A + B) + C , A,B,C M.

Ассоциативность сложения

2) 0 M | A + 0 = 0 + A = A, A M

3) N | A + N = N + A = 0, N= -A, A M

4) A+ B = B + A , A,B M

Коммутативность сложения

- абелева группа по сложению.

5)

6)

7)

8)

A,B M , , , 1 Р

Общее определение абстрактного векторного пространства.

V ≠ ; a, b, c є V; P-числовое поле.

Пусть: 1) Задана операция ∆, которая каждому a є V и каждому λ є P ставит в соответствие элемент λ∆a є V.

2) a,b є V задана операция □, которая каждой упорядоченной паре a,b є V ставит в соответствие единственный элемент a□b є V.

При этом выполняются 8 свойств (аксиом).

1.  a□(b□c)=(a□b)□c - ассоциативность

2. Ǝ z є V | ∀ a є V |a□z=z□a=a

3. ∀ a Ǝ n | n□a=a□n=z

1,2,3=>группа

4. a□b=b□a

1,2,3,4=>коммутативная группа

5. (α+β)∆a=(α∆a)□(β∆a)

6. α∆(a□b)= (α∆a)□(α∆ b)

7. α∆(β∆a)= (αβ)∆a

8.1∆a=a

∀ a, b є V; α,β є P; 1 є P

Тогда множество V называется векторным пространством над полем Р, операция □=+, ∆=умножение вектора на число, z-единичный элемент=0, а его элементы-векторы.

Линал

, n=0,1,2,3 - множество векторов в (на )

- точка (одноточечное множество)( )

- прямая ( )

- плоскость(планиметрия) ( )

- пространство(стереометрия) ( )