Для того, чтобы через три какие- либо точки пространства можно было провести единственную плоскость, необходимо, чтобы эти точки не лежали на одной прямой.

Рассмотрим точки М₁(x₁, y₁, z₁), M₂(x₂, y₂, z₂), M₃(x₃, y₃, z₃) в общей декартовой системе координат.

Для того, чтобы произвольная точка М(x, y, z) лежала в одной плоскости с точками М₁, М₂, М₃ необходимо, чтобы векторы были компланарны.

( ) = 0

Таким образом,

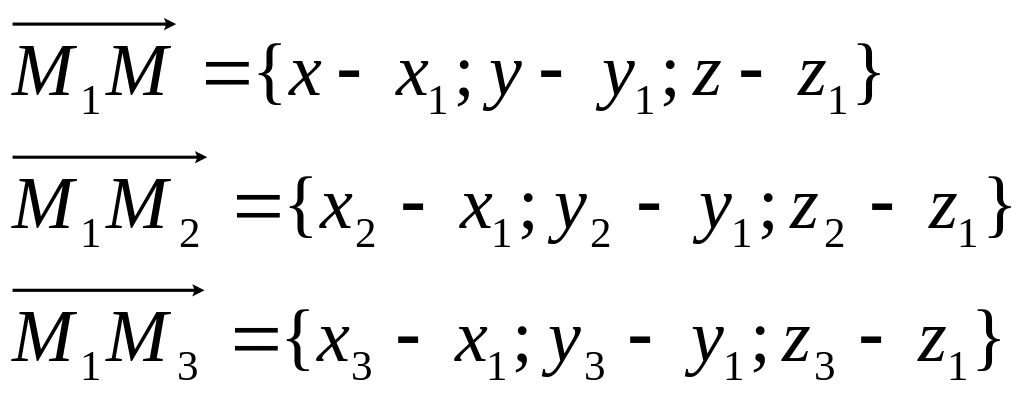
Уравнение плоскости, проходящей через три точки:

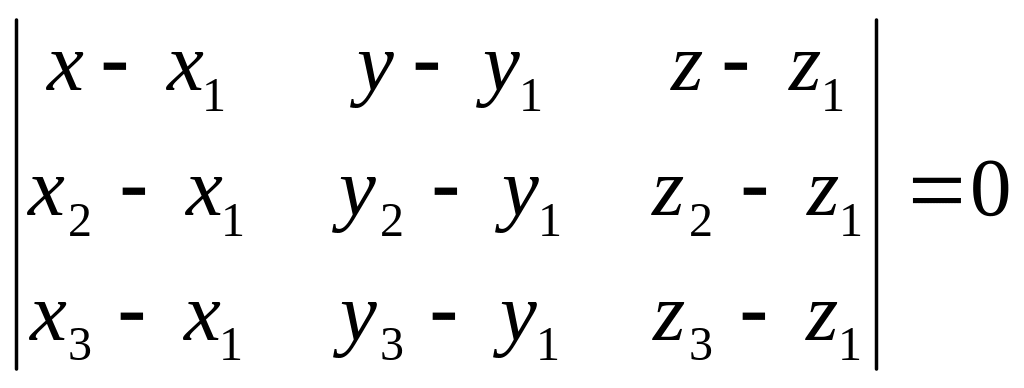
Уравнение плоскости по двум точкам и вектору, коллинеарному плоскости.

Пусть заданы точки м1(x1, y1, z1), m2(x2, y2, z2) и вектор .

Составим уравнение плоскости, проходящей через данные точки М₁ и М₂ и произвольную точку М(х, у, z) параллельно вектору .

Векторы и вектор должны быть компланарны, т.е.

( ) = 0

Уравнение плоскости:

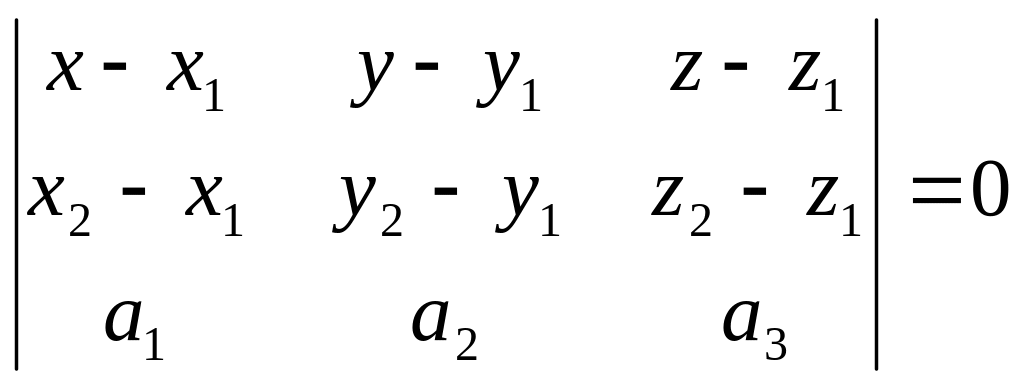
Уравнение плоскости по одной точке и двум векторам,

коллинеарным плоскости.

Пусть заданы два вектора и , коллинеарные плоскости. Тогда для произвольной точки м(х, у, z), принадлежащей плоскости, векторы должны быть компланарны.

Уравнение плоскости:

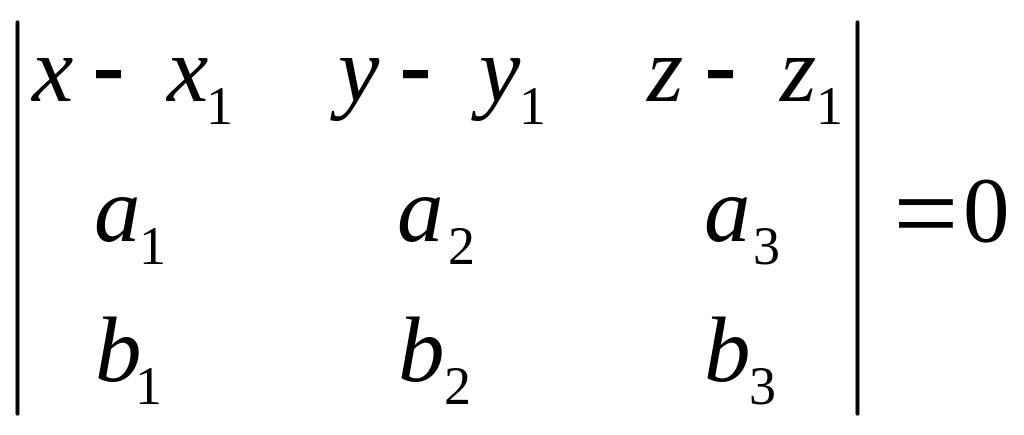
Уравнение плоскости по точке и вектору нормали.

Теорема. Если в пространстве задана точка М₀(х₀, у₀, z₀), то уравнение плоскости, проходящей через точку М₀ перпендикулярно вектору нормали (A, B, C) имеет вид: A(x – x₀) + B(y – y₀) + C(z – z₀) = 0.

Доказательство. Для произвольной точки М(х, у, z), принадлежащей плоскости, составим вектор . Т.к. вектор - вектор нормали, то он перпендикулярен плоскости, а, следовательно, перпендикулярен и вектору . Тогда скалярное произведение  = 0

Таким образом, получаем уравнение плоскости

Теорема доказана.

Уравнение плоскости в отрезках.

Если в общем уравнении Ах + Ву + Сz + D = 0 поделить обе части на –D: ,

заменив , получим уравнение плоскости в отрезках:

Числа a, b, c являются точками пересечения плоскости соответственно с осями х, у, z.

Уравнение плоскости в векторной форме. где

- радиус- вектор текущей точки М(х, у, z),

- единичный вектор, имеющий направление, перпендикуляра, опущенного на плоскость из начала координат.

,  и  - углы, образованные этим вектором с осями х, у, z.

p – длина этого перпендикуляра.

В координатах это уравнение имеет вид: xcos + ycos + zcos - p = 0.

Нормальным уравнением плоскости называется ее уравнение, написанное в виде , (1) где , , - направляющие косинусы нормали плоскоти, p - расстояние от начала координат до плоскости. При вычислении направляющих косинусов нормали следует считать, что она направлена от начала координат к плоскости (если же плоскость проходит через начало координат, то выбор положительного направления нормали безразличен).

Пусть - какая угодно точка пространства, d - расстояние от нее до данной плоскости. Отклонением точки от данной плоскости называется число +d, если точка и начало координат лежат по разные стороны от данной плоскости, и число -d, если они лежат по одну сторону от данной плоскости (если лежит на самой плоскости, то отклонение равно нулю).

Если точка имеет координаты , , , а плоскость задана нормальным уравнением , то отклонение точки от этой плоскости дается формулой .

Очевидно, . Общее уравнение плоскости приводится к нормальному виду (1) умножением на нормирующий множитель, определяемый формулой ; знак нормирующего множителя берется противоположным знаку свободного члена нормируемого уравнения.

БИЛЕТ № 50.

Экстремумы функции многих переменных.

1. Определение экстремума функции. Говорят, что функция f(x,y) имеет максимум (минимум) f(a,b) в точке P(a,b), если для всех отличных от Р точек P^/(x,y) в достаточно малой окрестности точки Р выполнено неравенство f(a,b)>f(x,y). Максимум или минимум функции называется ее экстремумом. Аналогично определяется экстремум функции трех и большего числа переменных.

2. Необходимые условия экстремума. Точки, в которых дифференцируемая функция f(x,y) может достигать экстремума (так называемые стационарные точки), находятся путем решения системы уравнений f^/_x(x,y)=0, f^/_y(x,y)=0 (1). (необходимые условия экстремума). Система (1) эквивалентна одному уравнению df(x,y)=0. В общем случае в точке экстремума P(a,b) функции f(x,y) или df(a,b)=0, или df(a,b) не существует.

3. Достаточные условия экстремума. Пусть P(a,b) – стационарная точка функции f(x,y), т.е. df(a,b)=0. Тогда: а) если d²f(a,b)<0 при dx²+dy²>0, то f(a,b) есть максимум функции f(х,у); б) если d²f(a,b)>0 при dx²+dy²>0, то f(a,b) есть минимум функции f(х,у); в) если d²f(a,b) меняет знак, то f(a,b) не является экстремумом функции f(х,у). Приведенные условия эквивалентны следующим: пусть f^/_x(a,b)=f^/_y(a,b)=0 и A=f^//_xx(a,b), B= f^//_xy(a,b), C=f^//_yy(a,b). Составим дискриминант =AC-B² ( >0). Если А>0 то минимум и если А<0 то максимум.

4. Случай функции многих переменных. Для функции трех и большего числа переменных необходимые условия существования экстремума аналогичны условиям 1⁰, (1), а достаточные условия аналогичны условиям 3⁰, а), б), в).

5. Условный экстремум. В простейшем случае условным экстремумом f(x,y) называется максимум или минимум этой функции, достигнутый при условии, что ее аргументы связаны уравнением q(x,y)=0 (уравнение связи). Чтобы найти условный экстремум функции f(x,y) при наличии соотношения g(x,y)=0, составляют так называемую функцию Лагранжа F(x,y)=f(x,y)+ *q(x,y), где - неопределенный постоянный множитель, и ищут обычный экстремум этой вспомогательной функции. 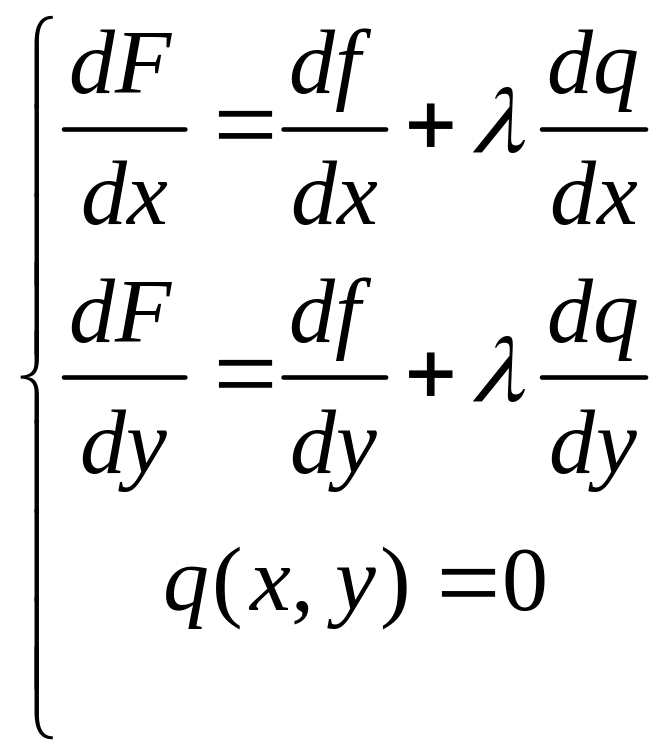Необходимые условия экстремума сводятся к системе трех уравнений: с тремя неизвестными x, y, , из которой можно определить эти неизвестные. Вопрос о существовании и характере условного экстремума решается на основании изучения знака второго дифференциала функций Лагранжа: .

6. Наибольшее и наименьшее значения функции. Функция, дифференцируемая в ограниченной замкнутой области, достигает своего наибольшего (наименьшего) значения или в стационарной точке, или в точке границы области.