
- •Э ллиптический параболоид: Гиперболический параболоид:
- •Трехосный эллипсоид:
- •Однополостный гиперболоид: д вуполостный гиперболоид:
- •К онус второго порядка:
- •Уравнение прямой в пространстве по точке и
- •Уравнение прямой в пространстве, проходящей через две точки.
- •Общие уравнения прямой в пространстве.
- •Для того, чтобы через три какие- либо точки пространства можно было провести единственную плоскость, необходимо, чтобы эти точки не лежали на одной прямой.
- •Пусть заданы точки м1(x1, y1, z1), m2(x2, y2, z2) и вектор .
- •Пусть заданы два вектора и , коллинеарные плоскости. Тогда для произвольной точки м(х, у, z), принадлежащей плоскости, векторы должны быть компланарны.
Уравнение прямой в пространстве по точке и
направляющему вектору.
Возьмем
произвольную прямую и вектор
![]() (m,
n, p),
параллельный данной прямой. Вектор
называется
направляющим вектором прямой.
(m,
n, p),
параллельный данной прямой. Вектор
называется
направляющим вектором прямой.
На прямой возьмем две произвольные точки М0(x0, y0, z0) и M(x, y, z).
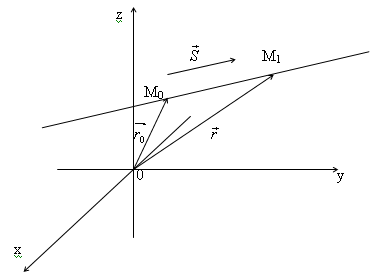
Обозначим
радиус- векторы этих точек как
![]() и
и
![]() ,
очевидно, что
-
=
,
очевидно, что
-
=
![]() .
.
Т.к. векторы и коллинеарны, то верно соотношение = t, где t – некоторый параметр.
Итого, можно записать: = + t.
Т.к. этому уравнению удовлетворяют координаты любой точки прямой, то полученное уравнение – параметрическое уравнение прямой.
Это векторное уравнение может быть представлено в координатной форме:
![]()
Преобразовав эту систему и приравняв значения параметра t, получаем канонические уравнения прямой в пространстве:
![]() .
.
Определение. Направляющими косинусами прямой называются направляющие косинусы вектора , которые могут быть вычислены по формулам:
![]() ;
;
![]()
![]() .
.
Отсюда получим: m : n : p = cos : cos : cos.
Числа m, n, p называются угловыми коэффициентами прямой. Т.к. - ненулевой вектор, то m, n и p не могут равняться нулю одновременно, но одно или два из этих чисел могут равняться нулю. В этом случае в уравнении прямой следует приравнять нулю соответствующие числители.
Уравнение прямой в пространстве, проходящей через две точки.
Если на прямой в пространстве отметить две произвольные точки M1(x1, y1, z1) и M2(x2, y2, z2), то координаты этих точек должны удовлетворять полученному выше уравнению прямой:
![]() .
.
Кроме того,
для точки М1 можно записать:
![]() .
.
Решая совместно
эти уравнения, получим:
![]() .
.
Это уравнение прямой, проходящей через две точки в пространстве.
Общие уравнения прямой в пространстве.
Уравнение прямой может быть рассмотрено как уравнение линии пересечения двух плоскостей.
Как было рассмотрено выше, плоскость в векторной форме может быть задана уравнением:
![]()
+
D = 0, где
+
D = 0, где
- нормаль плоскости; - радиус- вектор произвольной точки плоскости.
Пусть в
пространстве заданы две плоскости:
![]()
+
D1 = 0 и
+
D1 = 0 и
![]()
+
D2 = 0, векторы нормали
имеют координаты:
(A1,
B1, C1),
(A2,
B2, C2);
(x,
y, z).
+
D2 = 0, векторы нормали
имеют координаты:
(A1,
B1, C1),
(A2,
B2, C2);
(x,
y, z).
Тогда общие
уравнения прямой в векторной форме:
![]()
Общие уравнения
прямой в координатной форме:
![]()
Практическая задача часто состоит в приведении уравнений прямых в общем виде к каноническому виду.
Для этого надо найти произвольную точку прямой и числа m, n, p.
При этом направляющий вектор прямой может быть найден как векторное произведение векторов нормали к заданным плоскостям.
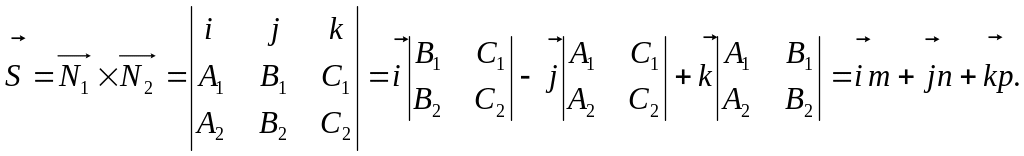
Пример. Найти каноническое уравнение, если прямая задана в виде:
![]()
Для нахождения произвольной точки прямой, примем ее координату х = 0, а затем подставим это значение в заданную систему уравнений.
![]() ,
т.е. А(0, 2, 1).
,
т.е. А(0, 2, 1).
Находим компоненты направляющего вектора прямой.
![]()
Тогда канонические уравнения прямой:
![]()
Пример. Привести к каноническому виду уравнение прямой, заданное в виде:
![]()
Для нахождения произвольной точки прямой, являющейся линией пересечения указанных выше плоскостей, примем z = 0. Тогда:
![]() ;
;
2x – 9x – 7 = 0;
x = -1; y = 3;
Получаем: A(-1; 3; 0).
Направляющий
вектор прямой:
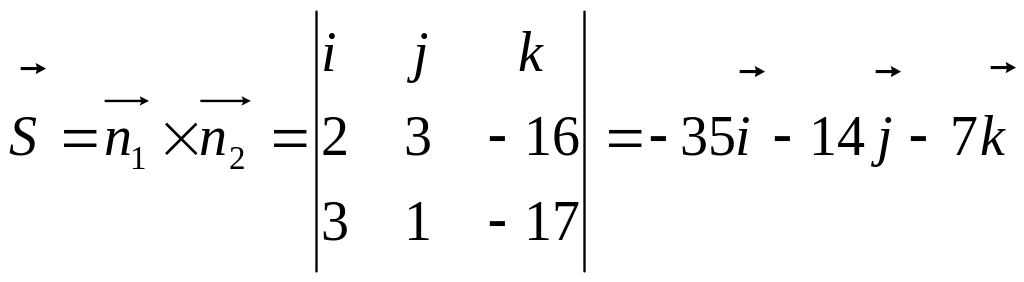 .
.
Итого:
![]()
БИЛЕТ № 22.
Наибольшие и наименьшие значения функции многих переменных.
Определение 1. Мы говорим, что функция z=f(x,y) имеет максимум в точке М(x0,y0) (т.е. при x=x0 и y=y0), если f(x0,y0)>f(x,y) для всех точек (x,y), достаточно близких к точке (x0, y0) и отличных от нее.
Определение 2. Совершенно аналогично говорят, что функция z=f(x,y) имеет минимум в точке М(x0, y0), если f(x0, y0)<f(x,y) для всех точек (x,y), достаточно близких к точке (x0, y0) и отличных от нее.
Максимум и минимум функции называются экстремумами функции, т.е. говорят, что функция имеет экстремум в данной точке, если эта функция имеет максимум или минимум в данной точке.
Теорема 1 (необходимые условия экстремума). Если функция z=f(x,y) достигает экстремума при x=x0, y=y0, то каждая частная производная первого порядка от z или обращается в нуль при этих значениях аргументов, или не существует.
Теорема 2. Пусть в некоторой области,
содержащей точку М(x0,y0),
функция f(x,y)
имеет непрерывные частные производные
до третьего порядка включительно; пусть,
кроме того, точка М(x0, y0)
является критической точкой функции
f(x,y),
т.е.
![]()
![]()
![]() .
Тогда при x=x0,
y=y0: 1) f(x,y)
имеет максимум, если
.
Тогда при x=x0,
y=y0: 1) f(x,y)
имеет максимум, если
 и
и
![]() ;
2) f(x,y)
имеет минимум, если
и
;
2) f(x,y)
имеет минимум, если
и
![]() ;
3) f(x,y)
не имеет ни максимума ни минимума, если
;
3) f(x,y)
не имеет ни максимума ни минимума, если
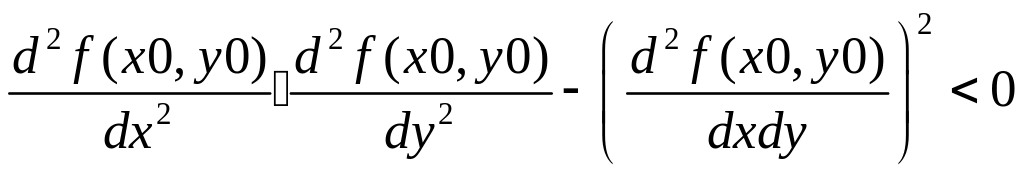 ;
4) если
;
4) если
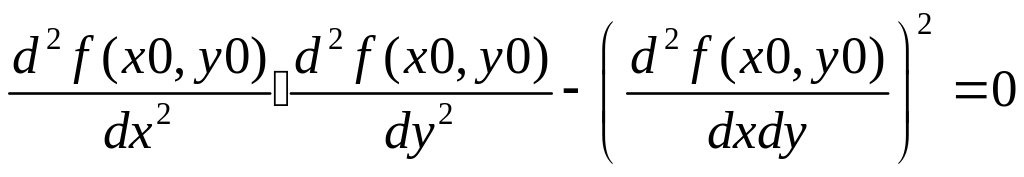 ,
то экстремум может быть и может не быть.
,
то экстремум может быть и может не быть.
БИЛЕТ № 23.
Кривые 2 порядка. Гипербола.
Определение. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная, меньшая расстояния между фокусами.
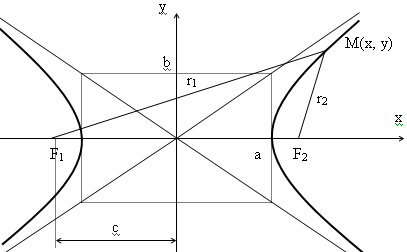
По определению r1 – r2= 2a. F1, F2 – фокусы гиперболы. F1F2 = 2c.
Выберем на гиперболе произвольную точку М(х, у). Тогда:
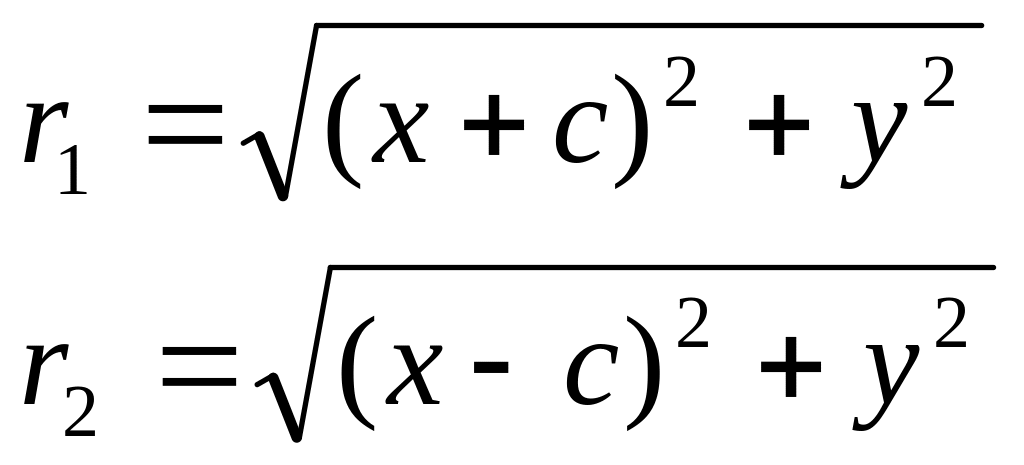
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
обозначим с2 – а2 = b2 (геометрически эта величина – меньшая полуось)
![]()
Получили каноническое уравнение гиперболы.
Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат.
Ось 2а называется действительной осью гиперболы.
Ось 2b называется мнимой осью гиперболы.
Гипербола
имеет две асимптоты, уравнения которых
![]()
Определение. Отношение
![]() называется
эксцентриситетом гиперболы, где с
– половина расстояния между фокусами,
а – действительная полуось.
называется
эксцентриситетом гиперболы, где с
– половина расстояния между фокусами,
а – действительная полуось.
С учетом того, что с2 – а2 = b2:
![]()
![]()
Если
а = b, e =
![]() ,
то гипербола называется равнобочной
(равносторонней).
,
то гипербола называется равнобочной
(равносторонней).
Определение. Две прямые,
перпендикулярные действительной оси
гиперболы и расположенные симметрично
относительно центра на расстоянии a/e
от него, называются директрисами
гиперболы. Их уравнения:
![]() .
.
Теорема. Если r – расстояние от произвольной точки М гиперболы до какого- либо фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r/d – величина постоянная, равная эксцентриситету.
Доказательство. Изобразим схематично гиперболу.
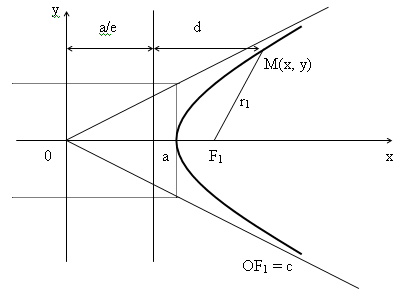
Из очевидных геометрических соотношений можно записать: a/e + d = x, следовательно d = x – a/e.
(x – c)2 + y2 = r2
Из канонического
уравнения:
![]() ,
с учетом b2 = c2
– a2:
,
с учетом b2 = c2
– a2:
![]()
![]()
![]()
Тогда т.к. с/a = e, то r = ex – a.
Итого:
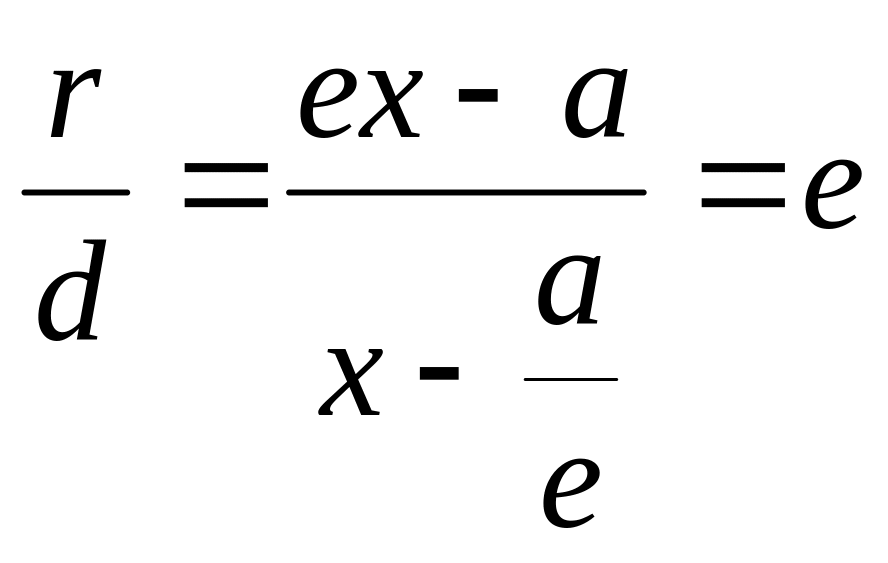 .
.
Для левой ветви гиперболы доказательство аналогично. Теорема доказана.
Пример.
Найти уравнение гиперболы, вершины и
фокусы которой находятся в соответствующих
вершинах и фокусах эллипса
![]() .
.
Для эллипса: c2 = a2 – b2.
Для гиперболы: c2 = a2 + b2.
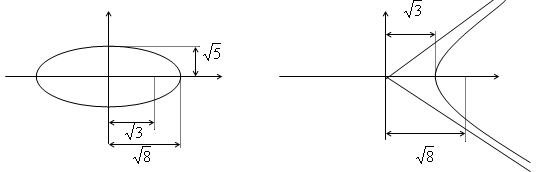
Уравнение
гиперболы:
![]() .
.
Пример.
Составить уравнение гиперболы, если ее
эксцентриситет равен 2, а фокусы совпадают
с фокусами эллипса с уравнением
![]() Находим фокусное расстояние c2
= 25 – 9 = 16.
Находим фокусное расстояние c2
= 25 – 9 = 16.
Для
гиперболы: c2
= a2 +
b2 =
16, e = c/a = 2; c = 2a; c2
= 4a2;
a2
= 4; b2
= 16 – 4 = 12. Итого:
![]() - искомое уравнение гиперболы.
- искомое уравнение гиперболы.
БИЛЕТ № 24.
Точка разрыва функции и их классификация.
Рассмотрим некоторую функцию f(x), непрерывную в окрестности точки х0, за исключением может быть самой этой точки. Из определения точки разрыва функции следует, что х = х0 является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной.
Следует отметить также, что непрерывность функции может быть односторонней. Поясним это следующим образом.
Если
односторонний предел (см. выше)
![]() ,
то функция называется непрерывной
справа.
,
то функция называется непрерывной
справа.

Если
односторонний предел (см. выше)
![]() ,
то функция называется непрерывной
слева.
,
то функция называется непрерывной
слева.
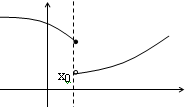
Определение. Точка х0 называется точкой разрыва функции f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке.
Определение. Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.
![]()
Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х0, достаточно того, что она определена слева и справа от нее.
Из определения можно сделать вывод, что в точке разрыва 1 – го рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 – го рода еще иногда называют устранимой точкой разрыва, но подробнее об этом поговорим ниже.
Определение. Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.
Пример. Функция Дирихле (Дирихле Петер Густав(1805-1859) – немецкий математик, член- корреспондент Петербургской АН 1837г)
![]()
не является непрерывной в любой точке х0.
Пример. Функция f(x) = имеет в точке х0 = 0 точку разрыва 2 – го рода, т.к.
![]() .
.
![]()
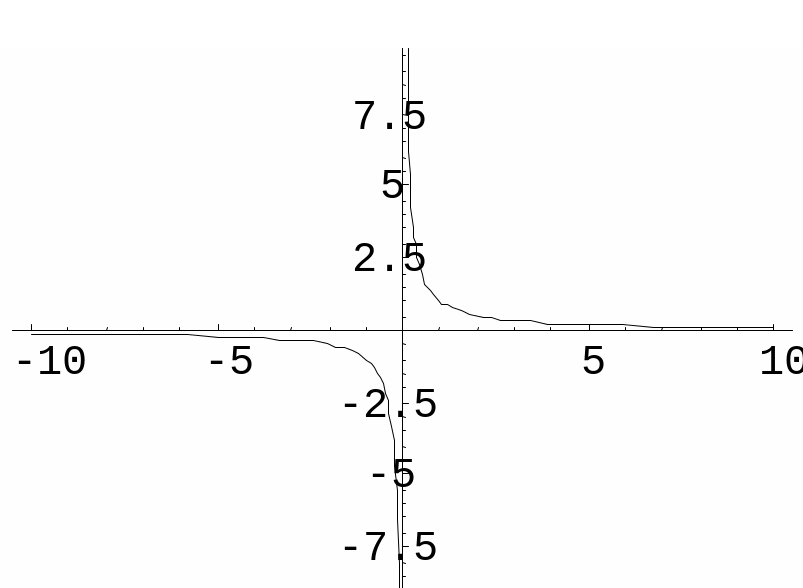
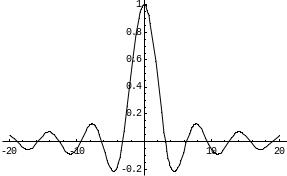
Пример.
f(x) =
![]()
Функция не
определена в точке х = 0, но имеет в ней
конечный предел
![]() ,
т.е. в точке х = 0 функция имеет точку
разрыва 1 – го рода. Это – устранимая
точка разрыва, т.к. если доопределить
функцию:
,
т.е. в точке х = 0 функция имеет точку
разрыва 1 – го рода. Это – устранимая
точка разрыва, т.к. если доопределить
функцию:
![]()
График этой функции:
Пример.
f(x) =
![]() =
=![]()
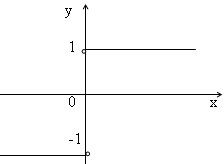
Эта функция также обозначается sign(x) – знак х. В точке х = 0 функция не определена. Т.к. левый и правый пределы функции различны, то точка разрыва – 1 – го рода. Если доопределить функцию в точке х = 0, положив f(0) = 1, то функция будет непрерывна справа, если положить f(0) = -1, то функция будет непрерывной слева, если положить f(x) равное какому- либо числу, отличному от 1 или –1, то функция не будет непрерывна ни слева, ни справа, но во всех случаях тем не менее будет иметь в точке х = 0 разрыв 1 – го рода. В этом примере точка разрыва 1 – го рода не является устранимой.
Таким образом, для того, чтобы точка разрыва 1 – го рода была устранимой, необходимо, чтобы односторонние пределы справа и слева были конечны и равны, а функция была бы в этой точке не определена.
БИЛЕТ № 25.
Линейная зависимость и независимость векторов. Разложение вектора по базису.
Линейная зависимость векторов.
Определение.
Векторы
![]() называются линейно зависимыми,
если существует такая линейная комбинация
называются линейно зависимыми,
если существует такая линейная комбинация
![]() ,
при не равных нулю одновременно i
, т.е.
,
при не равных нулю одновременно i
, т.е.
![]() .
.
Если же только при i = 0 выполняется , то векторы называются линейно независимыми.
Свойство
1. Если среди векторов
![]() есть нулевой вектор, то эти векторы
линейно зависимы.
есть нулевой вектор, то эти векторы
линейно зависимы.
Свойство 2. Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима.
Свойство 3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов.
Свойство 4. Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны.
Свойство 5. Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны.
Свойство 6. Любые 4 вектора линейно зависимы.
Рассмотрим пример на нахождение координат вектора.
Задача.
Даны векторы
![]() ,
,
![]() .
Вектор
.
Вектор
![]() --
медиана треугольника
--
медиана треугольника
![]() .
Найдите координаты вектора a в базисе
b, c.
.
Найдите координаты вектора a в базисе
b, c.
Решение. Сначала рассмотрим геометрическое решение (рис. 10.13).
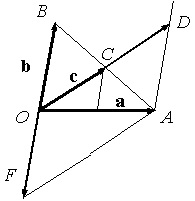
Проведем
через конец вектора a прямую
параллельно вектору b до пересечения
с продолжением вектора c. Получим
точку пересечения
![]() .
Легко видеть, что
.
Легко видеть, что
![]() ,
,
![]() .
Проведем через точку
.
Проведем через точку
![]() прямую
параллельно вектору c до пересечения
с продолжением вектора b. Получим
точку
прямую
параллельно вектору c до пересечения
с продолжением вектора b. Получим
точку
![]() .
Очевидно, что
.
Очевидно, что
![]() ,
то есть
,
то есть
![]() .
Таким образом,
.
Таким образом,
![]() .
Получим
.
Получим
![]() .
.
Аналитическое решение. Получим какое-нибудь уравнение, связывающее векторы a, b, c. Для этого достроим треугольник до параллелограмма (рис. 10.14).
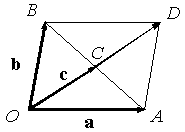
Тогда
,
![]() .
Получим равенство
.
Получим равенство
![]() .
Откуда
.
Откуда
![]() ,
то есть
.
Ответ:
,
то есть
.
Ответ:
БИЛЕТ № 26.
Полный дифференциал. Сложные функции многих переменных.
Определение: Полным дифференциалом функции z = f(x, y) называется главная линейная относительно х и у приращения функции z в точке (х, у).
![]()
Для функции произвольного числа переменных:
![]()
Пример.
Найти полный дифференциал функции
![]() .
.
![]()
![]()
![]()
Пример.
Найти полный дифференциал функции
![]()
![]()
![]()
![]()
БИЛЕТ № 27.
Нормальное уравнение прямой.
Если обе части
уравнения Ах + Ву + С = 0 разделить на число
![]() ,
которое называется нормирующем
множителем, то получим xcos
+ ysin
- p = 0 – нормальное уравнение
прямой.
,
которое называется нормирующем
множителем, то получим xcos
+ ysin
- p = 0 – нормальное уравнение
прямой.
Знак нормирующего множителя надо выбирать так, чтобы С < 0.
р – длина перпендикуляра, опущенного из начала координат на прямую, а - угол, образованный этим перпендикуляром с положительным направлением оси Ох.
Пример. Дано общее уравнение прямой 12х – 5у – 65 = 0. Требуется написать различные типы уравнений этой прямой.
уравнение
этой прямой в отрезках:
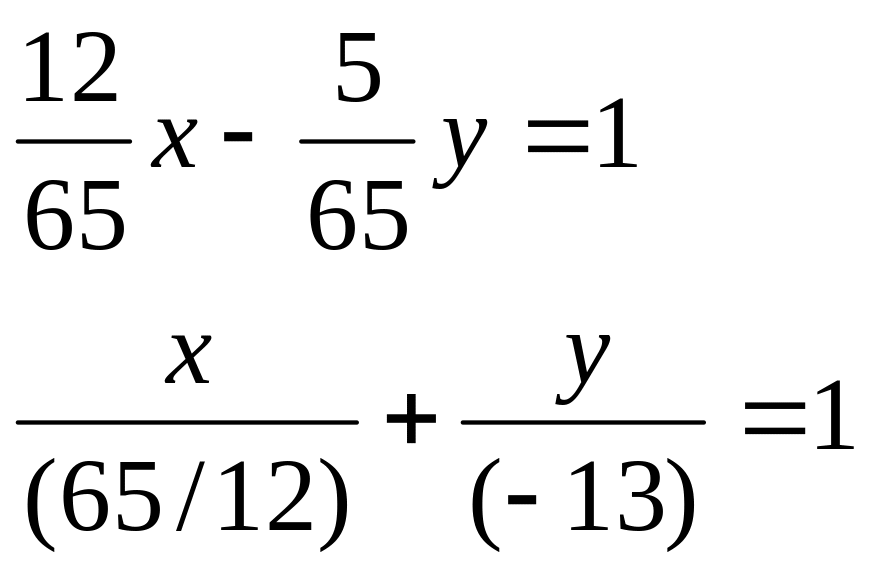
уравнение этой прямой с угловым коэффициентом: (делим на 5)
![]()
нормальное уравнение прямой:
![]() ;
cos
= 12/13; sin
= -5/13; p = 5.
;
cos
= 12/13; sin
= -5/13; p = 5.
Cледует отметить, что не каждую прямую можно представить уравнением в отрезках, например, прямые, параллельные осям или проходящие через начало координат.
Пример. Прямая отсекает на координатных осях равные положительные отрезки. Составить уравнение прямой, если площадь треугольника, образованного этими отрезками равна 8 см2.
Уравнение
прямой имеет вид:
![]() ,
a = b =
1; ab/2 = 8; a
= 4; -4.
,
a = b =
1; ab/2 = 8; a
= 4; -4.
a = -4 не подходит по условию задачи.
Итого:
![]() или х + у – 4 = 0.
или х + у – 4 = 0.
Пример. Составить уравнение прямой, проходящей через точку А(-2, -3) и начало координат.
Уравнение
прямой имеет вид:
![]() ,
где х1 = у1 = 0; x2
= -2; y2 = -3.
,
где х1 = у1 = 0; x2
= -2; y2 = -3.
![]()
Для самостоятельного решения: Составить уравнения прямых, проходящих через точку М(-3, -4) и параллельных осям координат.
Ответ: { x + 3 = 0; y + 4 = 0}.
БИЛЕТ № 28.
Геометрический и физический смысл производной.
Определение. Производной функции f(x) в точке х = х0 называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует.
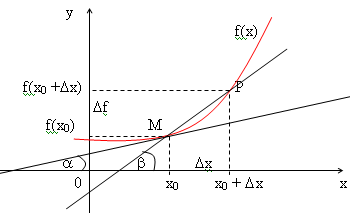
Пусть f(x)
определена на некотором промежутке (a,
b). Тогда
![]() тангенс угла наклона секущей МР к графику
функции.
тангенс угла наклона секущей МР к графику
функции.
![]() ,
,
где - угол наклона касательной к графику функции f(x) в точке (x0, f(x0)).
Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.
Уравнение касательной к кривой:
![]()
Уравнение
нормали к кривой:
![]() .
.
Фактически производная функции показывает как бы скорость изменения функции, как изменяется функция при изменении переменной.
Физический смысл производной функции f(t), где t- время, а f(t)- закон движения (изменения координат) – мгновенная скорость движения.
Соответственно, вторая производная функции- скорость изменения скорости, т.е. ускорение.
БИЛЕТ № 29.
Предмет и метод аналитической геометрии.
Аналити́ческая геоме́трия — раздел геометрии, в котором геометрические фигуры и их свойства исследуются средствами алгебры.
В основе этого метода лежит так называемый метод координат, впервые применённый Декартом. Каждому геометрическому соотношению этот метод ставит в соответствие некоторое уравнение, связывающее координаты фигуры или тела.
Аналитическая геометрия имеет также название координационная геометрия, которая раньше входила в рамки изучения декартовой геометрии. В целом же, аналитическая геометрия представляет собой учение о геометрии с использованием главных принципов алгебры. Алгебра, в основе изучения которой лежат действительные числа, в свою очередь может заниматься осуществлением линейного континуума в геометрии, используя аксиому Кантора-Дедекинда. Обычно декартова система координат используется для решения уравнения плоскости, уравнения прямых и площадей с известными значениями двух или трех координат. Согласно школьным учебникам, аналитическая геометрия занимается построением геометрических фигур с помощью вычислений и получением числовых значений, используя графическую информацию. Для вывода числовой информации также могут быть использованы вектор или форма. Некоторые в научных кругах полагают, что появление «продвинутой» аналитической геометрии по времени совпадает с появлением современной математики.
Известно, что греческий математик Менакмус занимался решением задач и доказательством теорем, используя метод, который был сопоставимым с тем, что используется в системах координат, изучающийся в рамках аналитической геометрии. У Апполония Пергии в работе над детерминированным сечением были проблемы, согласно аналитической геометрии, с определением числовых значений, нахождением координат на прямой, которые представлялись в непосредственной зависимости друг от друга. Позднее был выведен также метод, который являлся некой антитезой работе Декарта. Этот метод заключал: расстояние, измеряемое диаметром от точки касательной - это ось абсцисс, а отсекаемые отрезки, или, параллельные касательной оси, находящиеся между осями и кривой - ось ординат. В дальнейшем было определено соотношение между осью абсцисс и осью ординат, соответственно, вид которого представлялся эквивалентным уравнению кривой.
В 11в. персидский математик Омар Хайям заметил тесную взаимосвязь между геометрией и алгеброй и предпринял попытки закрыть просвет между числовой и геометрической алгеброй, использовав простое геометрическое решение — обычное уравнение третьей степени. Но весомый вклад Хайяма в области аналитической геометрии в дальнейшем был «перекрыт» открытиями Декарта.
До сих пор аналитическая геометрия традиционно отождествляется с деятельностью Рене Декарта, который много усилий приложил для изучения методов этого направления.
Абрахам де Муавр также занимался исследованием в области аналитической геометрии. Используя аксиому Кантора-Дедекинда, геометрия Евклида была интерпретирована на язык аналитической геометрии (то есть каждая теорема одного направления была преобразована в теорему другого).
Таким образом, представляется очевидным тот факт, что одни и те же методы и способы решения определенных задач, с учетом их специфики и интерпретации, могут быть использованы в различных областях математического знания.
БИЛЕТ № 30.
Полная производная сложной функции многих переменных.

БИЛЕТ № 31.
Смешанное произведение векторов.
Смешанное произведение векторов.
Определение.
Смешанным произведением векторов
![]() ,
,
![]() и
и
![]() называется число, равное скалярному
произведению вектора
на вектор, равный векторному произведению
векторов
и
.
называется число, равное скалярному
произведению вектора
на вектор, равный векторному произведению
векторов
и
.
Обозначается
![]() или
(
,
,
).
или
(
,
,
).
С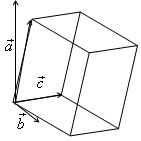 мешанное
произведение
по
модулю равно объему параллелепипеда,
построенного на векторах
,
и
.
мешанное
произведение
по
модулю равно объему параллелепипеда,
построенного на векторах
,
и
.
![]()
Свойства смешанного произведения:
1)Смешанное произведение равно нулю, если:
а)хоть один из векторов равен нулю;
б)два из векторов коллинеарны;
в)векторы компланарны.
2)![]() 3)
3)![]()
4)![]()
5) Объем
треугольной пирамиды, образованной
векторами
,
и
,
равен
![]()
6)Если
![]() ,
,
![]() ,
то
,
то
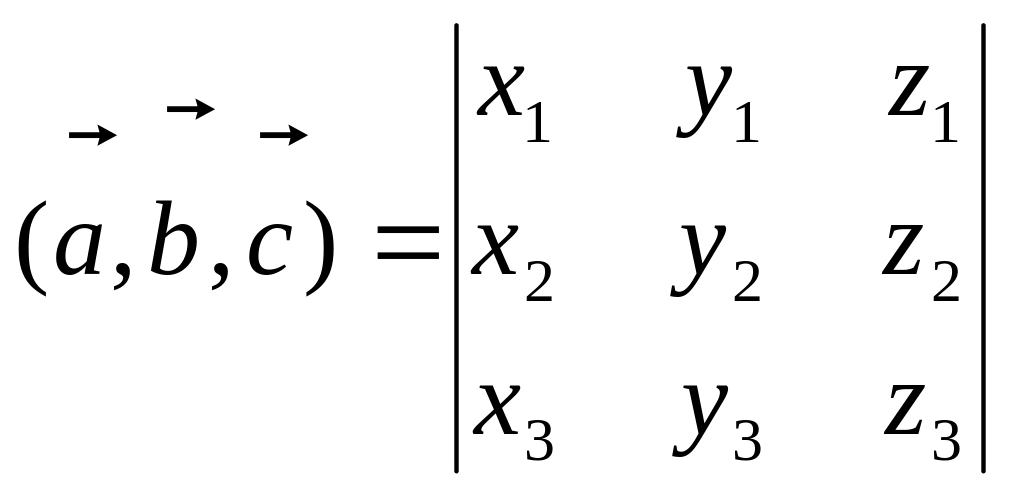
Пример. Доказать, что точки А(5; 7; 2), B(3; 1; -1), C(9; 4; -4), D(1; 5; 0) лежат в одной плоскости.
Найдем
координаты векторов:
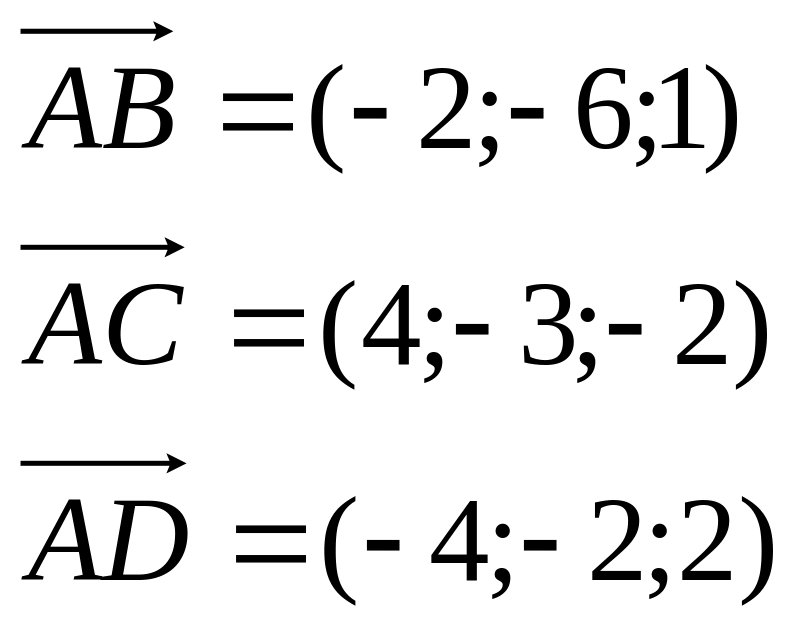
Найдем смешанное произведение полученных векторов:
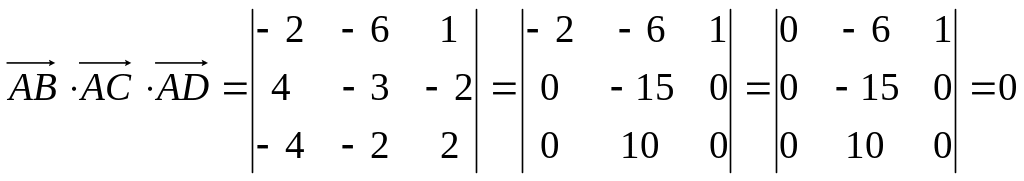 ,
,
Таким образом, полученные выше векторы компланарны, следовательно точки A, B, C и D лежат в одной плоскости.
Пример. Найти объем пирамиды и длину высоты, опущенной на грань BCD, если вершины имеют координаты A(0; 0; 1), B(2; 3; 5), C(6; 2; 3), D(3; 7; 2).
Найдем
координаты векторов:
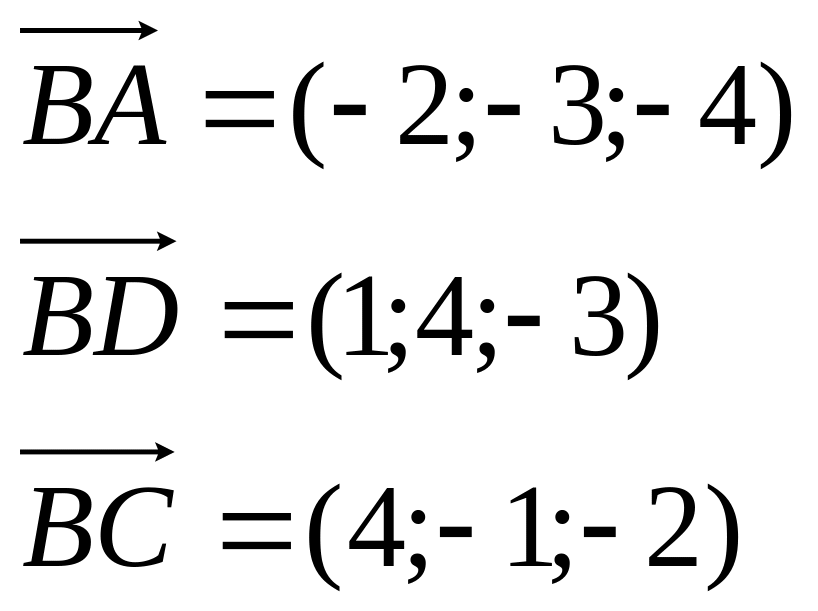
Объем пирамиды

Для нахождения длины высоты пирамиды найдем сначала площадь основания BCD.

![]()
Sосн
=
![]() (ед2)
Т.к. V =
(ед2)
Т.к. V =
![]() ;
;
![]() (ед)
(ед)
БИЛЕТ № 32.
Задачи, приводящие к производной.


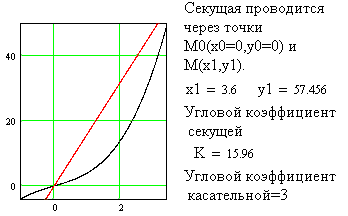

БИЛЕТ № 33.
Матрицы, основные понятия и определения.
Матрицей размером m на n, где m – число строк, n – число столбцов называется таблицей чисел, расположенных в определенном порядке, эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца на пересечении которых он находится. Элементы матрицы обозначаются aij, где I – номер строки, а j – номер столбца.
Матрица может состоять как из одной строки, так и из одного столбца. Вообще говоря матрица может состоять даже из одного элемента.
Определение 1. Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной.
Определение 2. Матрица вида: =
E, называется единичной
матрицей.
=
E, называется единичной
матрицей.
Определение 3. Если аm,n=an,m,
то матрица называется симметрической.
Пример:
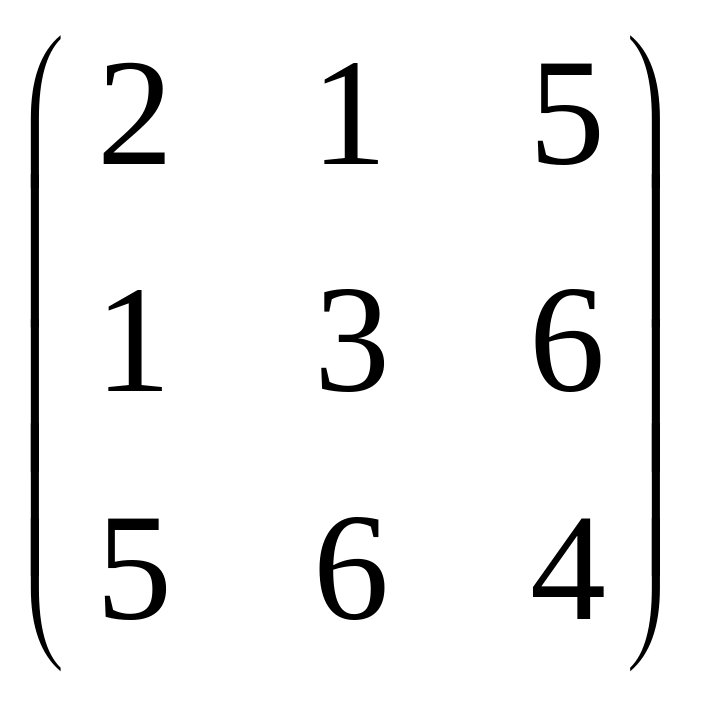 .
.
Определение 4. Квадратная матрица вида
 называется
диагональной матрицей.
называется
диагональной матрицей.
Самым главным свойством сложения и вычитания матриц является то, что они определены только для матрицы одинакового размера.
Матрица, полученная из матрицы А заменой
строк на столбцы, называется
транспонированной матрицей и обозначается
![]() .
.
Определение 5. Суммой (разностью) матриц является матрица элементами которой является соответственно сумма (разность) элементов сходных матриц. С = А + В = В + А.
Операция умножения (деления) матрицы любого размера это произвольное число сводится к умножению (делению) каждого элемента матрицы на это число.
Определение 6. Произведением матриц называется матрица элементы которой могут быть вычислены по след. формуле: А*В=С. Видно, что операция умножения матриц определена, когда число столбцов первой матрицы равно числу строк другой.
БИЛЕТ № 34.
Непрерывность функции.
Непрерывность функции на интервале и на отрезке.
Определение. Функция f(x) называется непрерывной на интервале (отрезке), если она непрерывна в любой точке интервала (отрезка).
При этом не требуется непрерывность функции на концах отрезка или интервала, необходима только односторонняя непрерывность на концах отрезка или интервала.
Свойства функций, непрерывных на отрезке.
Свойство 1: (Первая теорема Вейерштрасса (Вейерштрасс Карл (1815-1897)- немецкий математик)). Функция, непрерывная на отрезке, ограничена на этом отрезке, т.е. на отрезке [a, b] выполняется условие –M f(x) M.
Доказательство этого свойства основано на том, что функция, непрерывная в точке х0, ограничена в некоторой ее окрестности, а если разбивать отрезок [a, b] на бесконечное количество отрезков, которые “стягиваются” к точке х0, то образуется некоторая окрестность точки х0.
Свойство 2: Функция, непрерывная на отрезке [a, b], принимает на нем наибольшее и наименьшее значения.
Т.е. существуют такие значения х1 и х2, что f(x1) = m, f(x2) = M, причем m f(x) M
Отметим эти наибольшие и наименьшие значения функция может принимать на отрезке и несколько раз (например – f(x) = sinx).
Разность между наибольшим и наименьшим значением функции на отрезке называется колебанием функции на отрезке.
Свойство 3: (Вторая теорема Больцано – Коши). Функция, непрерывная на отрезке [a, b], принимает на этом отрезке все значения между двумя произвольными величинами.
Свойство 4: Если функция f(x) непрерывна в точке х = х0, то существует некоторая окрестность точки х0, в которой функция сохраняет знак.
Свойство 5: (Первая теорема Больцано (1781-1848) – Коши). Если функция f(x)- непрерывная на отрезке [a, b] и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого отрезка, где f(x) = 0.
Т.е. если sign(f(a)) sign(f(b)), то х0: f(x0) = 0.
Определение. Функция f(x) называется равномерно непрерывной на отрезке [a, b], если для любого >0 существует >0 такое, что для любых точек х1[a,b] и x2[a,b] таких, что х2 – х1<
верно неравенство f(x2) – f(x1) <
Отличие равномерной непрерывности от “обычной” в том, что для любого существует свое , не зависящее от х, а при “обычной” непрерывности зависит от и х.
Свойство 6: Теорема Кантора (Кантор Георг (1845-1918)- немецкий математик). Функция, непрерывная на отрезке, равномерно непрерывна на нем.
(Это свойство справедливо только для отрезков, а не для интервалов и полуинтервалов.)
Пример.
![]()
Функция непрерывна на интервале (0, а), но не является на нем равномерно непрерывной, т.к. существует такое число >0 такое, что существуют значения х1 и х2 такие, чтоf(x1) – f(x2)>, - любое число при условии, что х1 и х2 близки к нулю.
Свойство 7: Если функция f(x) определена, монотонна и непрерывна на некотором промежутке, то и обратная ей функция х = g(y) тоже однозначна, монотонна и непрерывна.
Пример. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.
![]()

в точке х = -1 функция непрерывна в точке х = 1 точка разрыва 1 – го рода

Пример. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.
![]()
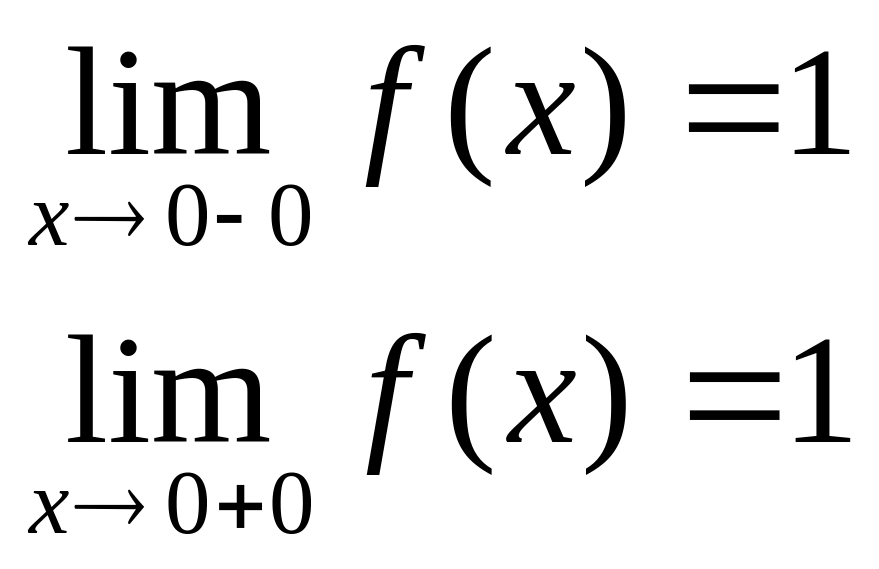
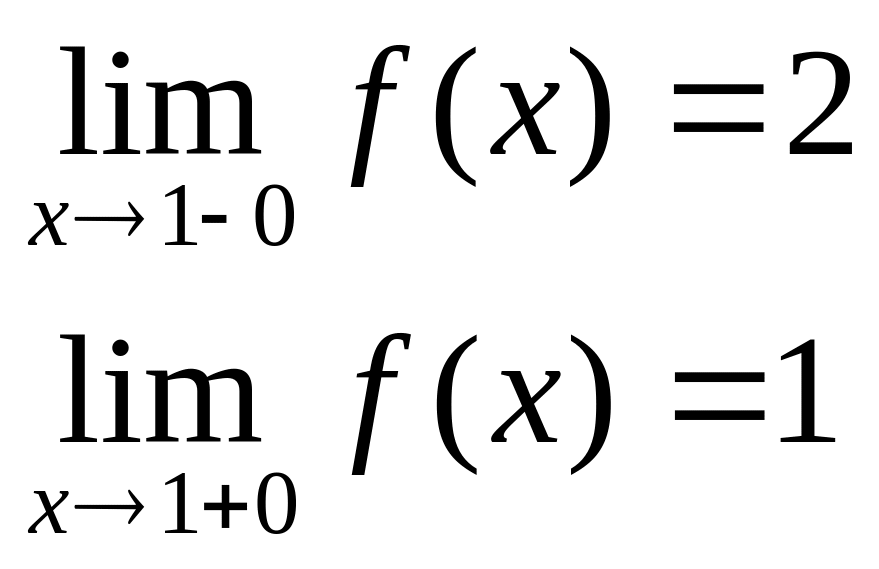
в точке х = 0 функция непрерывна в точке х = 1 точка разрыва 1 – го рода
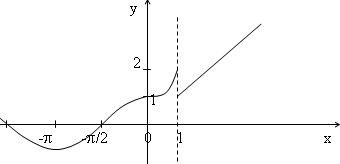
БИЛЕТ № 35.
Прямая на плоскости.
Определение. Любая прямая на плоскости может быть задана уравнением первого порядка Ах + Ву + С = 0, причем постоянные А, В не равны нулю одновременно, т.е. А2 + В2 0. Это уравнение первого порядка называют общим уравнением прямой.
В зависимости от значений постоянных А,В и С возможны следующие частные случаи:
C = 0, А 0, В 0 – прямая проходит через начало координат
А = 0, В 0, С 0 { By + C = 0}- прямая параллельна оси Ох
В = 0, А 0, С 0 { Ax + C = 0} – прямая параллельна оси Оу
В = С = 0, А 0 – прямая совпадает с осью Оу
А = С = 0, В 0 – прямая совпадает с осью Ох
Уравнение прямой по точке и вектору нормали. Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой , заданной уравнением Ах + Ву + С = 0.
Пример. Найти уравнение прямой,
проходящей через точку А(1, 2) перпендикулярно
вектору
![]() (3,
-1).
(3,
-1).
Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А.
Получаем: 3 – 2 + C = 0, следовательно С = -1.
Итого: искомое уравнение: 3х – у – 1 = 0.
Уравнение прямой, проходящей через две точки. Пусть в пространстве заданы две точки M1(x1, y1, z1) и M2(x2, y2, z2), тогда уравнение прямой, проходящей через эти точки:
На плоскости
записанное выше уравнение прямой
упрощается:
![]()
если х1 х2 и х = х1, еслих1 = х2.
Дробь
![]() =
k называется угловым
коэффициентом прямой.
=
k называется угловым
коэффициентом прямой.
Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4). Применяя записанную выше формулу, получаем:
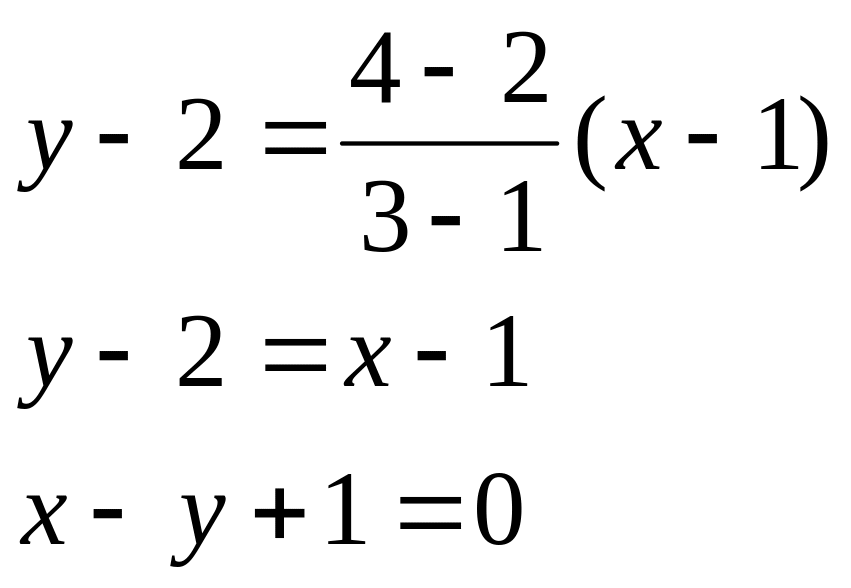
Уравнение
прямой по точке и угловому коэффициенту.
Если общее уравнение прямой Ах
+ Ву + С = 0 привести к виду:
![]() и обозначить
и обозначить
![]() ,
то полученное уравнение называется
уравнением прямой с угловым коэффициентом
k.
,
то полученное уравнение называется
уравнением прямой с угловым коэффициентом
k.
Уравнение прямой по точке и направляющему вектору.
По аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание прямой через точку и направляющий вектор прямой.
Определение. Каждый ненулевой вектор (1, 2), компоненты которого удовлетворяют условию А1 + В2 = 0 называется направляющим вектором прямой
Ах + Ву + С = 0.
Уравнение
прямой в отрезках. Если в общем
уравнении прямой Ах + Ву + С = 0 С
0, то, разделив на –С, получим:![]() или
или
![]() ,
где
,
где
![]()
Пример. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках.
С = 1,
![]() ,
а = -1, b = 1.
,
а = -1, b = 1.
Нормальное уравнение прямой. Если обе части уравнения Ах + Ву + С = 0 разделить на число , которое называется нормирующем множителем, то получим xcos + ysin - p = 0 – нормальное уравнение прямой.
Знак нормирующего множителя надо выбирать так, чтобы С < 0.
р – длина перпендикуляра, опущенного из начала координат на прямую, а - угол, образованный этим перпендикуляром с положительным направлением оси Ох.
Пример. Дано общее уравнение прямой 12х – 5у – 65 = 0. Требуется написать различные типы уравнений этой прямой.
уравнение этой прямой в отрезках:
уравнение этой прямой с угловым коэффициентом: (делим на 5)
нормальное уравнение прямой: ; cos = 12/13; sin = -5/13; p = 5.
Угол между
прямыми на плоскости. Определение.
Если заданы две прямые y
= k1x
+ b1, y
= k2x
+ b2, то острый угол
между этими прямыми будет определяться
как
![]() .
.
Две прямые параллельны, если k1 = k2. Две прямые перпендикулярны, если k1 = -1/k2.
Теорема. Прямые Ах + Ву + С = 0 и А1х + В1у + С1 = 0 параллельны, когда пропорциональны коэффициенты А1 = А, В1 = В. Если еще и С1 = С, то прямые совпадают.
Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой.
Определение.
Прямая, проходящая через точку М1(х1,
у1) и перпендикулярная к прямой у
= kx + b
представляется уравнением:
![]()
БИЛЕТ № 36.
Частные производные сложной функции многих переменных.
Очень часто при решении практических задач (например, в высшей геодезии или аналитической фотограмметрии) появляются сложные функции нескольких переменных, т. е. аргументы x, y, z одной функции f (x,y,z)) сами являются функциями от новых переменных U, V, W).
Так, например, бывает при переходе от неподвижной системы координат Oxyz в подвижную систему O0UVW и обратно. При этом важно знать все частные производные по "неподвижным" - "старым" и "подвижным" - "новым" переменным, так как эти частные производные обычно характеризуют положение объекта в этих системах координат, и, в частности, влияют на соответствие аэрофотоснимков реальному объекту. В таких случаях применяются следующие формулы:

То есть задана сложная функцияT трех "новых" переменных U, V, W посредством трёх "старых" переменных x, y, z, тогда:

Замечание. Возможны вариации в количестве переменных. Например: если

то
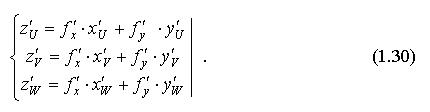
В частности, еслиz = f(xy), y = y(x) , то получаем так называемую формулу "полной производной":

Эта же формула "полной производной" в случае:
![]()
примет вид:
![]()
Возможны и иные вариации формул (1.27) - (1.32).
Замечание: формула "полной производной" используется в курсе физики, раздел "Гидродинамика" при выводе основополагающей системы уравнений движения жидкости.
Пример 1.10. Дано:
![]() Найти
Найти
![]()
Решение Согласно (1.31):
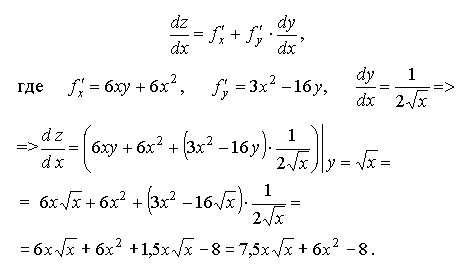
Ответ:
![]()
БИЛЕТ № 37.
Линейные операции над векторами.
Суммой
![]() двух
векторов
двух
векторов
![]() и
и
![]() называется
вектор, который идет из начала вектора
в
конец вектора
при
условии, что вектор
приложен
к концу вектора
(правильно
треугольника). Построение суммы
изображено
на рис. 1.
называется
вектор, который идет из начала вектора
в
конец вектора
при
условии, что вектор
приложен
к концу вектора
(правильно
треугольника). Построение суммы
изображено
на рис. 1.
Н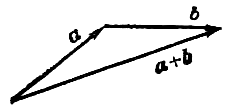 аряду
с правилом треугольника часто пользуются
(равносильным ему) правилом параллелограмма:
если векторы
и
приведены
к общему началу и на них построен
параллелограмм, то сумма
есть
вектор, совпадающий с диагональю этого
паралеллограмма, идущей из общего начала
и
(рис.
2). Отсюда сразу следует, что
аряду
с правилом треугольника часто пользуются
(равносильным ему) правилом параллелограмма:
если векторы
и
приведены
к общему началу и на них построен
параллелограмм, то сумма
есть
вектор, совпадающий с диагональю этого
паралеллограмма, идущей из общего начала
и
(рис.
2). Отсюда сразу следует, что
![]() .
.
С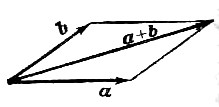 ложение
многих векторов производится при помощи
последовательного применения правила
треугольника (см. рис. 3, где изображено
построение суммы четырех векторов
,
,
ложение
многих векторов производится при помощи
последовательного применения правила
треугольника (см. рис. 3, где изображено
построение суммы четырех векторов
,
,
![]() ,
,
![]() ).
).
Р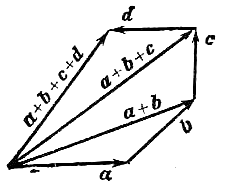 азность
азность
![]() двух
векторов
и
называется
вектор, который в сумме с вектором
составляет
вектор
.
Если два вектора
и
приведены
к общему началу, то разность их
есть
вектор, идущий из конца
(«вычитаемого»)
к концу
(«уменьшаемого»).
Два вектора равной длины, лежащие на
одной прямой и направленные в
противоположные стороны, называются
взаимно обратными: если один из них
обозначен символом
,
то другой обозначается символом
двух
векторов
и
называется
вектор, который в сумме с вектором
составляет
вектор
.
Если два вектора
и
приведены
к общему началу, то разность их
есть
вектор, идущий из конца
(«вычитаемого»)
к концу
(«уменьшаемого»).
Два вектора равной длины, лежащие на
одной прямой и направленные в
противоположные стороны, называются
взаимно обратными: если один из них
обозначен символом
,
то другой обозначается символом
![]() .
Легко видеть, что
.
Легко видеть, что
![]() .
Таким образом, построение разности
равносильно прибавлению к «уменьшаемому»
вектора, обратного «вычитаемого».
.
Таким образом, построение разности
равносильно прибавлению к «уменьшаемому»
вектора, обратного «вычитаемого».
Произведение
![]() (или
также
(или
также
![]() )
вектора
на
число
)
вектора
на
число
![]() называется
вектор, модуль которого равен произведению
модуля вектора
на
модуль числа
;
он параллелен вектору
или
лежит с ним на одной прямой и направлен
так же, как вектор
,
если
-
число положительное, и противоположно
вектору
,
если
-
число отрицательное.
называется
вектор, модуль которого равен произведению
модуля вектора
на
модуль числа
;
он параллелен вектору
или
лежит с ним на одной прямой и направлен
так же, как вектор
,
если
-
число положительное, и противоположно
вектору
,
если
-
число отрицательное.
Сложение векторов и умножение вектора на число называются линейными операциями над векторами.
Имеют место следующие две основные теоремы о проекциях векторов:
1). Проекция суммы векторов на какую-нибудь
ось равна сумме ее проекций на эту же
ось:
![]()
2). При умножении вектора на число его
проекция умножается на то же число:
![]() .
.
В частности, если
![]() ,
,
![]() ,
то
,
то
![]() ,
и
,
и
![]() .
Если
.
Если
![]() ,
то для любого числа
,
то для любого числа
![]() .
.
Векторы, лежащие на одной прямой или на
параллельных прямых, называются
коллинеарными. Признаком коллинеарности
двух векторов
,
,
является пропорциональность их координат:
![]() .
.
Тройка векторов
![]() ,
,
![]() ,
,
![]() называется
координатным базисом, если эти векторы
удовлетворяют следующим условиям:
называется
координатным базисом, если эти векторы
удовлетворяют следующим условиям:
1). Вектор лежит на оси Ох, вектор - на оси Оу, вектор - на оси Oz;
2). Каждый из векторов , , направлен по своей оси в положительную сторону;
3). Векторы
,
,
единичные,
то есть
![]() ,
,
![]() ,
,
![]() .
.
Каким бы ни был вектор
,
он всегда может быть разложен по базису
,
,
,
то есть может быть представлен в виде
![]() ;
коэффициенты этого разложения являются
координатами вектора
(то
есть X, Y, Z суть проекции вектора
на
координатные оси).
;
коэффициенты этого разложения являются
координатами вектора
(то
есть X, Y, Z суть проекции вектора
на
координатные оси).
БИЛЕТ № 38.
Теорема Ролля, Лагранжа, Каши.
Теорема Роля: Если функция f(x) непрерывна на отрезке [a, b], дифференцируема на интервале (а, b) и значения функции на концах отрезка равны f(a) = f(b), то на интервале (а, b) существует точка , a < < b, в которой производная функция f(x) равная нулю, f() = 0.
Теорема Ролля имеет несколько следствий:
Если функция f(x) на отрезке [a, b] удовлетворяет теореме Ролля, причем f(a) = f(b) = = 0, то существует по крайней мере одна точка , a < < b, такая, что f() = 0. Т.е. между двумя нулями функции найдется хотя бы одна точка, в которой производная функции равна нулю.
Если на рассматриваемом интервале (а, b) функция f(x) имеет производную (n-1)- го порядка и n раз обращается в нуль, то существует по крайней мере одна точка интервала, в котором производная (n – 1) – го порядка равна нулю.
Теорема
Лагранжа: Если функция f(x)
непрерывна на отрезке [a,
b] и дифференцируема
на интервале (а, b),
то на этом интервале найдется по крайней
мере одна точка :
a <
< b, такая, что
![]() .
.
Теорема Коши: Если функции f(x) и g(x) непрерывны на отрезке [a, b] и дифференцируемы на интервале (a, b) и g(x) 0 на интервале (a, b), то существует по крайней мере одна точка , a < < b, такая, что
![]() .
.
Т.е. отношение приращений функций на данном отрезке равно отношению производных в точке .
БИЛЕТ № 39.
Скалярное произведение векторов.
Определение. Скалярным произведением векторов и называется число, равное произведению длин этих сторон на косинус угла между ними.
= cos
Свойства скалярного произведения:
= 2;
= 0, если или = 0 или = 0.
= ;
( +
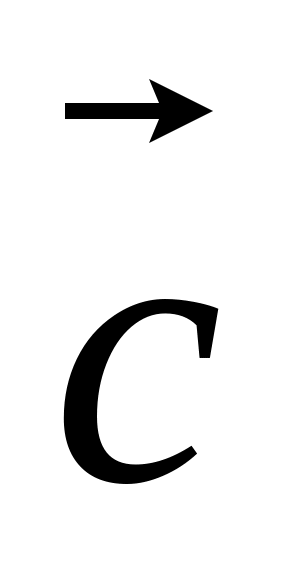 )
=
+
;
)
=
+
;(m ) = (m ) = m( );
Если рассматривать векторы
![]() в
декартовой прямоугольной системе
координат, то
= xa
xb
+ ya
yb
+ za
zb;
в
декартовой прямоугольной системе
координат, то
= xa
xb
+ ya
yb
+ za
zb;
Используя полученные равенства, получаем формулу для вычисления угла между векторами:
![]() ;
;
Пример.
Найти (5
+ 3
)(2
-
),
если
![]()
10
-
5
+
6
-
3
= 10![]() ,
,
т.к.
![]() .
.
Пример.
Найти угол между векторами
и
,
если
![]()
![]() .
.
Т.е. = (1, 2, 3), = (6, 4, -2)
= 6 + 8 – 6 = 8:
![]() .
.
cos
=
![]()
Пример.
Найти скалярное произведение (3
- 2
)(5
- 6
),
если
![]()
15
-
18
-
10
+
12
= 15![]()
+ 1236 = 240 – 336 + 432 = 672 – 336 = 336.
Пример.
Найти угол между векторами
и
,
если
![]()
![]() .
.
Т.е. = (3, 4, 5), = (4, 5, -3)
= 12 + 20 - 15 =17 :
![]() .
.
cos
=
![]()
Пример.
При каком m векторы
![]() и
и
![]() перпендикулярны.
перпендикулярны.
=
(m, 1, 0);
=
(3, -3, -4)
![]() .
.
Пример.
Найти скалярное произведение векторов
![]() и
и
![]() ,
если
,
если
![]()
(
)(
)
=
![]()
![]()
![]() =
10 +
=
10 +
+ 27 + 51 + 135 + 72 + 252 = 547.
БИЛЕТ № 40.
Градиент. Производная по направлению.
Определение: Если в некоторой области D задана функция u = u(x, y, z) и некоторый вектор, проекции которого на координатные оси равны значениям функции u в соответствующей точке
![]() ,
то этот вектор называется градиентом
функции u.
,
то этот вектор называется градиентом
функции u.
![]()
Связь градиента с производной по направлению. Теорема: Пусть задана функция u = u(x, y, z) и поле градиентов .
Тогда производная
![]() по направлению некоторого вектора
по направлению некоторого вектора
![]() равняется проекции вектора gradu
на вектор
.
равняется проекции вектора gradu
на вектор
.
Доказательство:
Рассмотрим единичный вектор
![]() и некоторую функцию u =
u(x, y,
z) и найдем скалярное
произведение векторов
и gradu.
и некоторую функцию u =
u(x, y,
z) и найдем скалярное
произведение векторов
и gradu.
![]()
Выражение, стоящее в правой части этого равенства является производной функции u по направлению s.
Т.е.
![]() .
Если угол между векторами gradu
и
обозначить через ,
то скалярное произведение можно записать
в виде произведения модулей этих векторов
на косинус угла между ними. С учетом
того, что вектор
единичный, т.е. его модуль равен единице,
можно записать:
.
Если угол между векторами gradu
и
обозначить через ,
то скалярное произведение можно записать
в виде произведения модулей этих векторов
на косинус угла между ними. С учетом
того, что вектор
единичный, т.е. его модуль равен единице,
можно записать:
![]()
Выражение, стоящее в правой части этого равенства и является проекцией вектора gradu на вектор .
БИЛЕТ № 41.
Векторное произведение векторов.
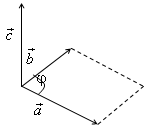
Определение. Векторным произведением векторов и называется вектор , удовлетворяющий следующим условиям:
1)
![]() ,
где - угол между
векторами
и
,
,
где - угол между
векторами
и
,
![]()
2) вектор ортогонален векторам и
3) , и образуют правую тройку векторов.
Обозначается:
![]() или
или![]() .
.
Свойства векторного произведения векторов:
1)
![]() ;
;
2)
![]() ,
если
или
=
0 или
=
0;
,
если
или
=
0 или
=
0;
3) (m ) = (m ) = m( );
4) ( + ) = + ;
5) Если заданы
векторы
(xa,
ya,
za)
и
(xb,
yb,
zb)
в декартовой прямоугольной системе
координат с единичными векторами
![]() ,
то
,
то
=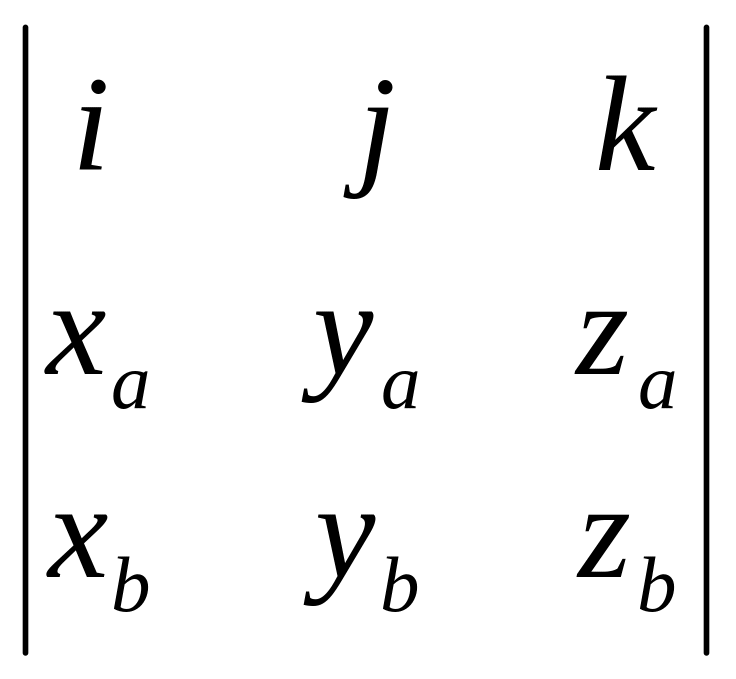
6) Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах и .
Пример. Вычислить площадь треугольника с вершинами А(2, 2, 2), В(4, 0, 3),
С(0, 1, 0).
![]()
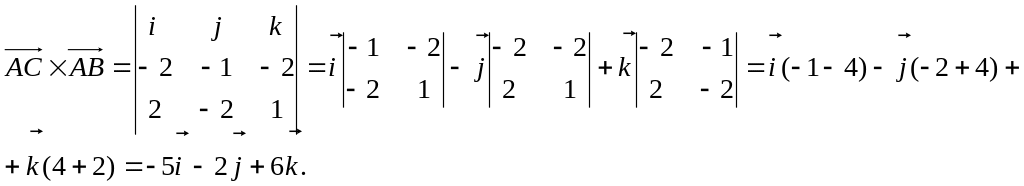
![]()
![]() (ед2).
(ед2).
Пример.
Доказать, что векторы
![]() ,
,
![]() и
и
![]() компланарны.
компланарны.
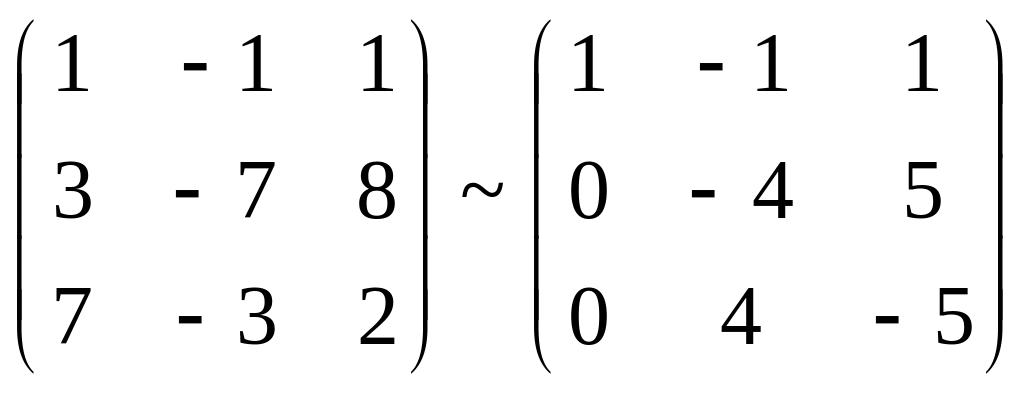 ,
т.к. векторы линейно зависимы, то они
компланарны.
,
т.к. векторы линейно зависимы, то они
компланарны.
Пример.
Найти площадь параллелограмма,
построенного на векторах
![]() ,
если
,
если
![]()
![]()
![]() (ед2).
(ед2).
БИЛЕТ № 42.
Дифференциалы высших порядков для функции многих переменных.




БИЛЕТ № 43.
Теорема Кронекера-Капелли.
Теорема: Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.
RgA = RgA*.
Очевидно, что система (1) может быть записана в виде:
x1![]() + x2
+ x2
![]() +
… + xn
+
… + xn
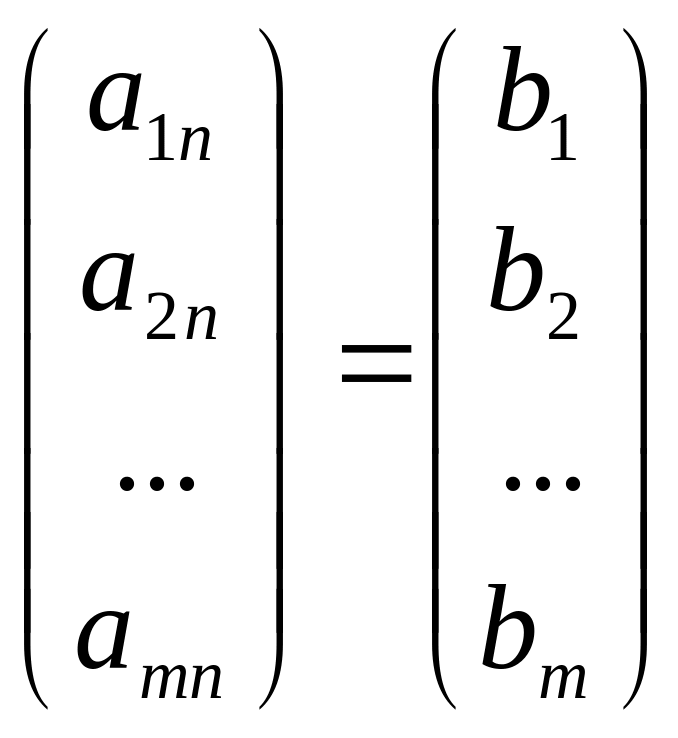
Доказательство.
1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход АА* не изменяют ранга.
2) Если RgA = RgA*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.
Пример. Определить совместность системы линейных уравнений:
![]()
A
=
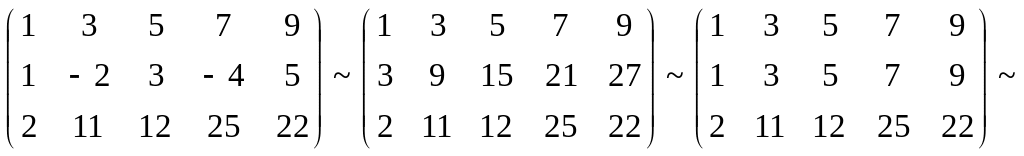
~
![]() .
.
![]() RgA = 2.
RgA = 2.
A*
=
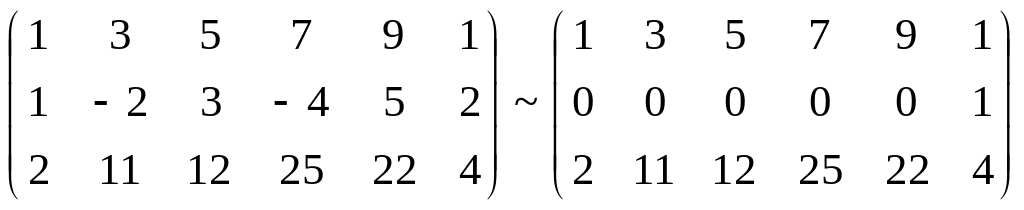 RgA* = 3.
RgA* = 3.
Система несовместна.
Пример. Определить совместность системы линейных уравнений.
![]() А =
А =
 ;
;
![]() = 2 + 12 = 14
0; RgA = 2;
= 2 + 12 = 14
0; RgA = 2;
A*
=

![]() RgA* = 2.
RgA* = 2.
Система совместна. Решения: x1 = 1; x2 =1/2.
БИЛЕТ № 44.
Уравнение касательной к плоскости и нормали к поверхности.
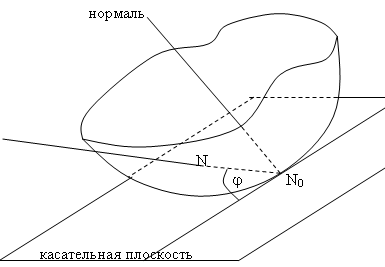
Пусть N и N0 – точки данной поверхности. Проведем прямую NN0. Плоскость, которая проходит через точку N0, называется касательной плоскостью к поверхности, если угол между секущей NN0 и этой плоскостью стремится к нулю, когда стремится к нулю расстояние NN0.
Определение. Нормалью к поверхности в точке N0 называется прямая, проходящая через точку N0 перпендикулярно касательной плоскости к этой поверхности.
В какой – либо точке поверхность имеет, либо только одну касательную плоскость, либо не имеет ее вовсе.
Если поверхность
задана уравнением z = f(x,
y), где f(x,
y) – функция, дифференцируемая
в точке М0(х0, у0),
касательная плоскость в точке
N0(x0,y0,(x0,y0))
существует и имеет уравнение:
![]() .
.
Уравнение нормали к
поверхности в этой точке:
![]()
БИЛЕТ № 45.
Ранг матрицы.
Определение. В матрице порядка mn минор порядка r называется базисным, если он не равен нулю, а все миноры порядка r+1 и выше равны нулю, или не существуют вовсе, т.е. r совпадает с меньшим из чисел m или n.
Столбцы и строки матрицы, на которых стоит базисный минор, также называются базисными.
В матрице может быть несколько различных базисных миноров, имеющих одинаковый порядок.
Определение. Порядок базисного минора матрицы называется рангом матрицы и обозначается Rg А.
Очень важным свойством элементарных преобразований матриц является то, что они не изменяют ранг матрицы.
Определение. Матрицы, полученные в результате элементарного преобразования, называются эквивалентными.
Надо отметить, что равные матрицы и эквивалентные матрицы - понятия совершенно различные.
Теорема. Наибольшее число линейно независимых столбцов в матрице равно числу линейно независимых строк.
Т.к. элементарные преобразования не изменяют ранг матрицы, то можно существенно упростить процесс нахождения ранга матрицы.
Пример. Определить ранг матрицы.
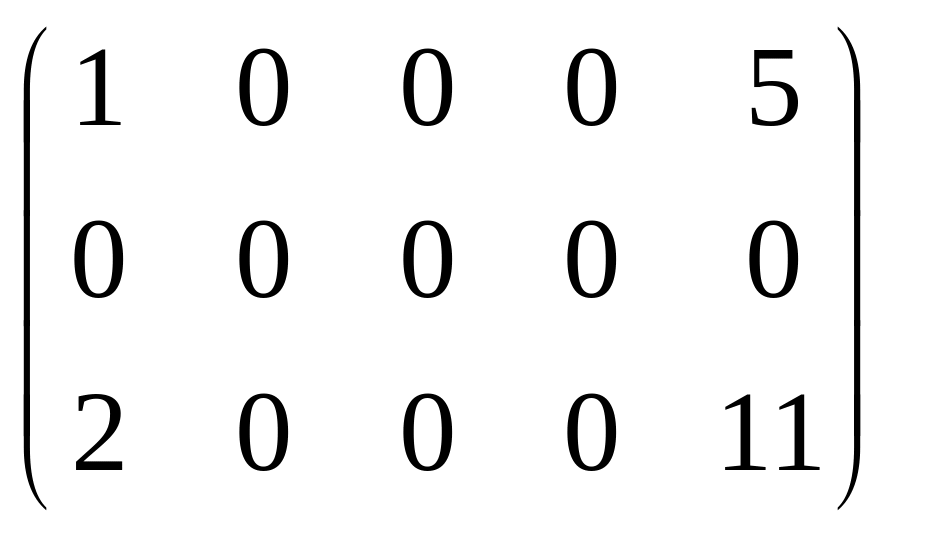
![]()
![]() ,
,
![]() RgA = 2.
RgA = 2.
Пример: Определить ранг матрицы.
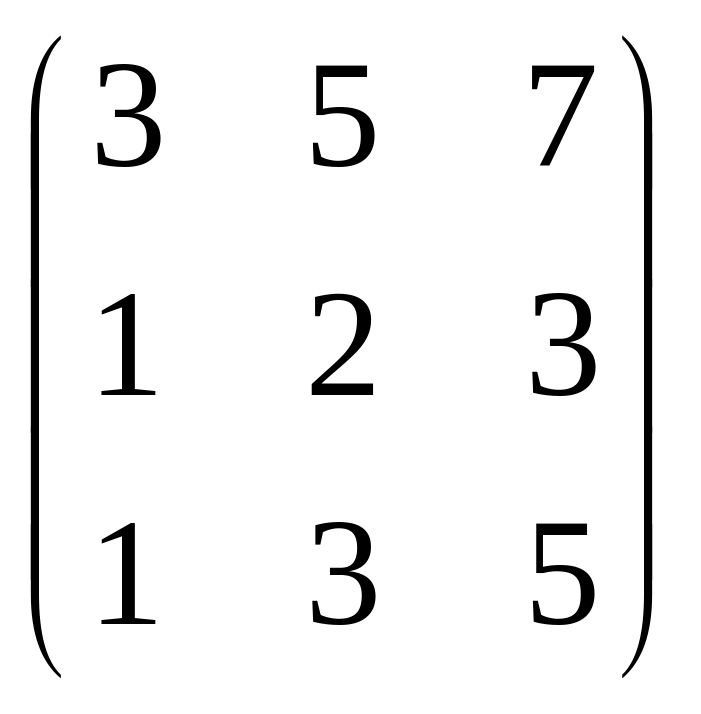
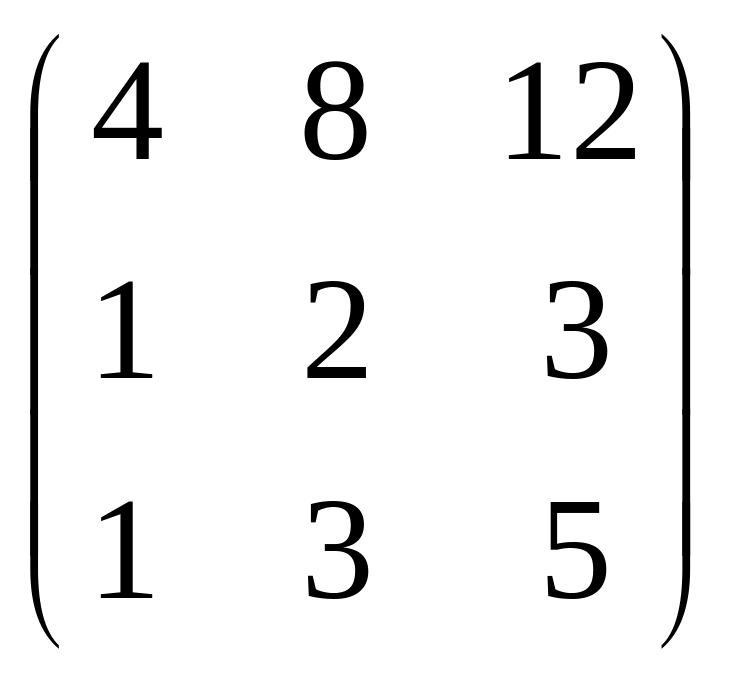
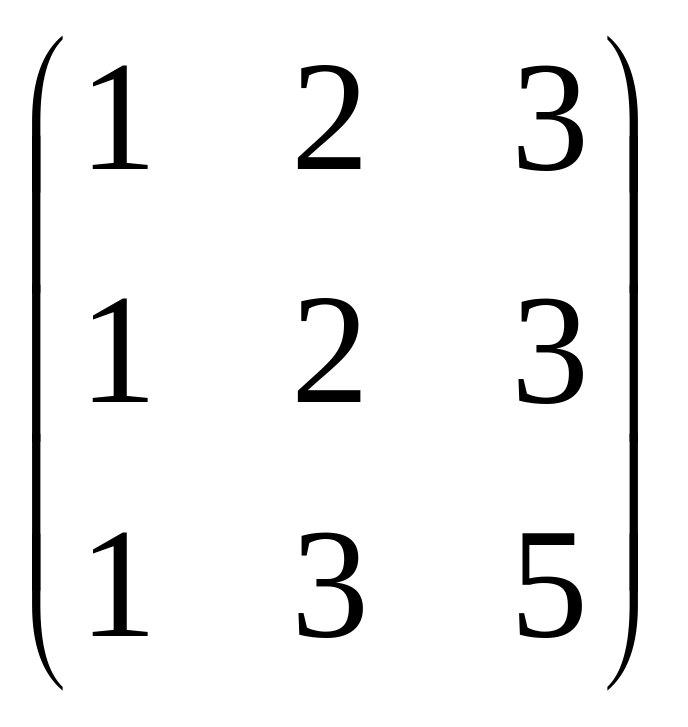
![]() ,
,
![]() Rg = 2.
Rg = 2.
Пример. Определить ранг матрицы.

![]() ,
,
![]()
Rg = 2.
Rg = 2.
Если с помощью элементарных преобразований не удается найти матрицу, эквивалентную исходной, но меньшего размера, то нахождение ранга матрицы следует начинать с вычисления миноров наивысшего возможного порядка. В вышеприведенном примере – это миноры порядка 3. Если хотя бы один из них не равен нулю, то ранг матрицы равен порядку этого минора.
БИЛЕТ № 46.
Применение дифференциалов в приближенных вычислениях.
Пусть нам известно значение функции y0=f(x0) и ее производной y0' = f '(x0) в точке x0. Покажем, как найти значение функции в некоторой близкой точке x.
Как мы уже выяснили приращение функции Δyможно представить в виде суммы Δy=dy+α·Δx, т.е. приращение функции отличается от дифференциала на величину бесконечно малую. Поэтому, пренебрегая при малых Δx вторым слагаемым в приближенных вычислениях, иногда пользуются приближенным равенством Δy≈dyили Δy»f'(x0)·Δx.
Т.к., по определению, Δy = f(x) – f(x0), то f(x) – f(x0)≈f'(x0)·Δx. Откуда f(x) ≈ f(x0) + f'(x0)·Δx
Примеры.
1. y = x2 – 2x. Найти приближенно, с помощью дифференциала, изменение y (т.е. Δy), когда x изменяется от 3 до 3,01. Имеем Δy≈dy=f'(x)·Δx. f'(x)=2x – 2 ,f'(3)=4, Δx=0,01. Поэтому Δy ≈ 4·0,01 = 0,04.
Вычислить приближенно значение функции
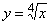 в
точке x = 17.
в
точке x = 17.
Пусть x0= 16. Тогда Δx = x
– x0= 17 – 16 = 1,
![]() ,
,
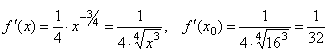 .
Таким образом,
.
Таким образом,
![]() .
.
Вычислить ln 0,99.
Будем рассматривать это значение как частное значение функции y=lnx при х=0,99.
Положим x0 = 1. Тогда Δx
= – 0,01, f(x0)=0.
![]() ,
f '(1)=1.Поэтому f(0,99) ≈ 0 – 0,01 = –
0,01.
,
f '(1)=1.Поэтому f(0,99) ≈ 0 – 0,01 = –
0,01.
БИЛЕТ № 47.
Цилиндрические поверхности.
Определение. Цилиндрическими поверхностями называются поверхности, образованные линиями, параллельными какой- либо фиксированной прямой.
Рассмотрим поверхности, в уравнении которых отсутствует составляющая z, т.е. направляющие параллельны оси Оz. Тип линии на плоскости ХOY (эта линия называется направляющей поверхности) определяет характер цилиндрической поверхности. Рассмотрим некоторые частные случаи в зависимости от уравнения направляющих:
- эллиптический цилиндр.
2 ) - гиперболический цилиндр.
x2 = 2py – параболический цилиндр.
БИЛЕТ № 48.
Дифференциал функции нескольких переменных.


БИЛЕТ № 49.
Уравнение плоскости. Нормальное уравнение плоскости.
Определение.
Плоскостью называется поверхность,
вес точки которой удовлетворяют общему
уравнению: Ax + By
+ Cz + D = 0, где
А, В, С – координаты вектора
![]() -вектор
нормали к плоскости. Возможны
следующие частные случаи:
-вектор
нормали к плоскости. Возможны
следующие частные случаи:
А = 0 – плоскость параллельна оси Ох
В = 0 – плоскость параллельна оси Оу
С = 0 – плоскость параллельна оси Оz
D = 0 – плоскость проходит через начало координат
А = В = 0 – плоскость параллельна плоскости хОу
А = С = 0 – плоскость параллельна плоскости хОz
В = С = 0 – плоскость параллельна плоскости yOz
А = D = 0 – плоскость проходит через ось Ох
В = D = 0 – плоскость проходит через ось Оу
С = D = 0 – плоскость проходит через ось Oz
А = В = D = 0 – плоскость совпадает с плоскостью хОу
А = С = D = 0 – плоскость совпадает с плоскостью xOz
В = С = D = 0 – плоскость совпадает с плоскостью yOz
Уравнение плоскости, проходящей через три точки.
