3.4. Освещенность

Освещенность представляет собой поверхностную плотность светового потока, падающего на освещаемую поверхность. При равномерном распределении светового потока F в пре­делах освещаемой поверхности S значение освещенности можно определить как:

E = F/S. (1.3.12)

Освещенность и сила света точечного источника света при нормальном падении лучей (поверхность перпендикулярна лучам) связаны следующим соотноше­нием:

E = I/r², (1.3.13)

где r – расстояние от источника света до освещаемой поверхнос­ти.

Это выражение называется законом квадратов расстоя­ний. Его сформулировал еще в 1604 г. немецкий астроном Иоганн Кеплер. Следует помнить, что освещенность будет оставаться постоянной вдоль пучка лучей только тогда, когда они параллельны.

Если лучи от источника падают на поверхность под углом j к нормали (рис.1.3.6), то тот же световой поток F распределяется по площади, в 1/cosj раз большей, чем S (по площади S/cosj) и формула примет вид:

E = I∙cosj /r². (1.3.14)

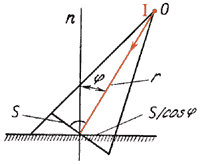
Рис. 1.3.6 – К определению освещенности поверхности

Закон квадратов расстояний приемлем для расчета освещеннос­ти, создаваемой осветительными приборами, но минимальное значение r определя­ется таким параметром осветительного прибора как рабочее расстоя­ние. Следует добавить, что освещенность поверхности может созда­ваться не одним источником, как показано на рис.1.3.5, а любым числом произвольно расположенных источников, посылающих свет на освещаемую поверхность (или ее элемент) с различных направ­лений и под разными углами к ее нормали. Тогда общая освещенность будет равна сумме освещенностей поверхности в данной точ­ке от различных источников света:

E =E₁ + E₂ + E₃ +…+ E_n. (1.3.15)

Эта формула представляет собой закон аддитивности, из которого следует, что общая освещенность равна сумме освещенностей поверхности в данной точ­ке от различных источников света.

Единицей освещенности является люкс (лк, от лат. lux - свет).

Таким образом, единица освещенности один люкс равна такой поверхностной плотности светового потока, при которой световой поток один люмен приходится на один квадратный метр: 1 лк = 1 лм/1 м². Внесистемная единица освещенности: 1фот = 1лм /1см². В США, Англии и других странах в качестве еди­ницы освещенности часто используется фут-кандела: 1 фут-кандела = 1 лм/1 фут² = 10,764 лк.

3.5. Яркость

Яркость поверхности изотропных излучателей для заданного направления – это отношение силы света, излучаемого в данном на­правлении, к площади проекции светящейся поверхности на плоскость, перпендикулярную к этому направлению (рис.1.3.7):

L = I/Scosj. (1.3.16)

При равномерном освещении диффузно отражающей поверхности уравнение, связывающее яркость этой поверхности с ее освещенно­стью будет иметь вид:

L = rE/p, (1.3.17)

где r – коэффициент отражения поверхности.

Яркость – единственная из световых величин, которую глаз воспринимает непосредственно, и при отсутствии поглощения света в среде распространения, она не зависит от расстояния. Уравнение, связывающее яркость объекта L, освещенность E_зр, созда­ваемую этим объектом на зрачке глаза, и телесный угол w, в пределах которого глаз видит данный объект, можно представить как:

L = E_зр /w. (1.3.18)

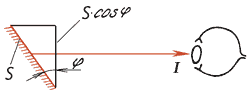
Рис. 1.3.7 – К определению яркости поверхности

Таким образом, при удалении глаза от объекта, освещенность E_зр на его зрачке снижается, при этом одновременно уменьшается телес­ный угол w, но значение яркости L остается неизменным (рис.1.3.8).

Единицей яркости является кандела на квадратный метр (кд/м²). 1 кд/м² – это яркость такой плоской поверхности, кото­рая в перпендикулярном направлении излучает силу света в 1 кд с 1 м² поверхности.

До принятия системы СИ в качестве единицы яркости использовали нит (нт, от лат. niteo - блещу, сверкаю), численно эта единица эквивалентна кд/м². Другой несистемной единицей является стильб (от греческого stilbio – сверкаю, сияю):

1 сб = 10000 нт = 10000 кд/м².

Часто в качестве несистемной единицы для измерения и расче­та яркости отражающих свет поверхностей используется апостильб: 1 асб = 1/p кд/м². Один апостильб - это яркость абсолютно белой, диффузно отражающей поверхности, имеющей освещенность, равную 1 люкс. При рас­четах яркости диффузно отражающей поверхности в апостильбах яркость рассчитывается по формуле:

L = rE. (1.3.19)

В США в качестве несистемной единицы яркости широко используется ламберт (лб), получившая свое название в честь немецкого ученого И.Ламберта. Коэффициенты для пересчета различных единиц яркости приведены в табл.1.3.3.

Таблица 1.3.3. Коэффициенты для пересчета различных единиц яркости

Единицы яркости	кд/м2	Асб	сб	лб	кд/ф2	фут-лб	мллб
Кандела/кв.м	1	3,14	0,0001	0,000314	0,0929	0,2919	0,3142
Апостильб	0,318	1	0,000032	0,0001	0,0296	0,0929	0,1
Стильб	10000	31416	1	3,14	929	2919	3142
Ламберт	3183	10000	0,318	1	296	929	1000
Миллиламберт	3,18	10	0,000318	0,001	0,296	0,929	1
Фут-ламберт	3,43	10,764	0,000343	0,0011	0,318	1	1,0764
Кандела/кв.фут	10,764	33,82	0,0011	0,0034	1	3,14	3,382