
- •9. Основы специальной теории относительности
- •9.1 Введение
- •9.2 Пространство и время в ньютоновской механике
- •9.3 Опыт Майкельсона и Морли
- •9.4 Постулаты Эйнштейна
- •9.4 Одновременность событий
- •9.5 Пространство-время
- •9.6 Замедление времени
- •9.7 Лоренцево сокращение
- •9.8 Преобразования Лоренца
- •9.9 Релятивистский импульс
9.9 Релятивистский импульс
В
классической механике импульс определяется
как
![]() .
Импульс замкнутой системы частиц
сохраняется во времени в любой ИСО.
.
Импульс замкнутой системы частиц
сохраняется во времени в любой ИСО.
Для замкнутой системы релятивистских частиц закон сохранения импульса в ньютоновской форме не выполняется. В этом можно убедиться на примере абсолютно неупругого удара двух одинаковых шаров массы m в системах К и К’. (Савельев, т.1, стр.233) Например, при неупругом соударении двух одинаковых по массе частиц, движущихся навстречу друг другу с одинаковой скоростью получим для К системы, что полный импульс системы до и после столкновения равен нулю, т.е. в К системе он сохраняется.
Рассмотрим
то же соударение в К’ системе. По формуле
преобразования скорости найдем для
![]() и для
и для
![]() ,
а для скоростей шаров после соударения
одинаковые скорости (по той же формуле),
равные
.
Значит суммарный импульс до соударения
равен
,
а для скоростей шаров после соударения
одинаковые скорости (по той же формуле),
равные
.
Значит суммарный импульс до соударения
равен
![]() ,
а после:
,
а после:
![]() .
Т.е., закон сохранения импульса не
выполняется.
.
Т.е., закон сохранения импульса не
выполняется.
Возникает дилемма: либо отказаться от ньютоновского определения импульса, либо от закона сохранения импульса. Учитывая важнейшую роль законов сохранения, за фундаментальный закон в теории относительности принимают закон сохранения импульса и уже из него находят выражение для самого импульса.
Выражение
для импульса находят в таком виде, чтобы
закон сохранения был инвариантен по
отношению к преобразованиям Лоренца.
При этом при малых скоростях v
c
релятивистское выражение для импульса
должно переходить в ньютоновское
![]() .
.
Предполагают, что выражение для импульса частицы массы m в релятивистской механике должно иметь вид:
![]() где
где
![]() -
некоторая безразмерная функция скорости,
-
некоторая безразмерная функция скорости,
![]() -скорость,
а
-
модуль скорости частицы. Очевидно, что
при v
c
функция
практически равна единице. Требование
выполнения закона сохранения импульса
в любой ИСО и учет релятивистского
преобразования скорости при переходе
от одной ИСО к другой приводит к выводу,
что импульс частицы должен зависеть от
ее скорости более сложным образом:
-скорость,
а
-
модуль скорости частицы. Очевидно, что
при v
c
функция
практически равна единице. Требование
выполнения закона сохранения импульса
в любой ИСО и учет релятивистского
преобразования скорости при переходе
от одной ИСО к другой приводит к выводу,
что импульс частицы должен зависеть от
ее скорости более сложным образом:
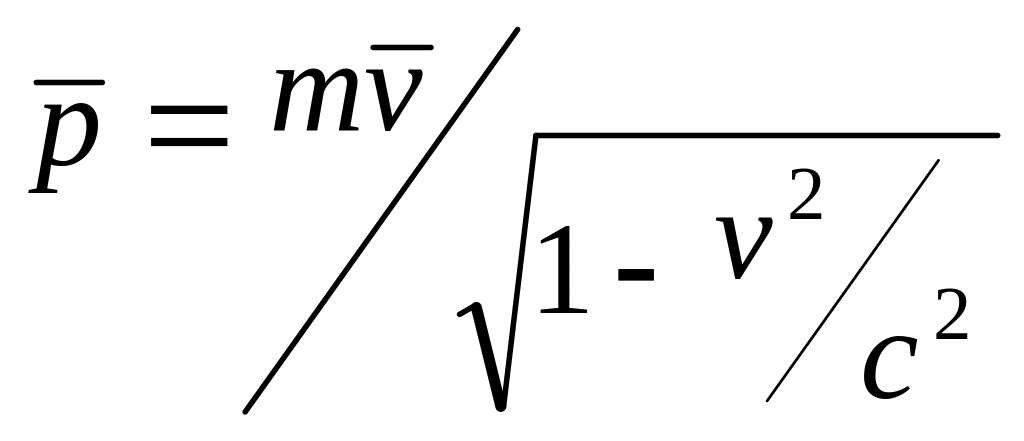 .
.
При v c это выражение переходит в ньютоновское определение импульса.
Этот
импульс подчиняется закону сохранения
во всех ИСО. Графики
![]() для релятивистской и ньютоновской
механики показаны на рис. 9.6.
для релятивистской и ньютоновской
механики показаны на рис. 9.6.
З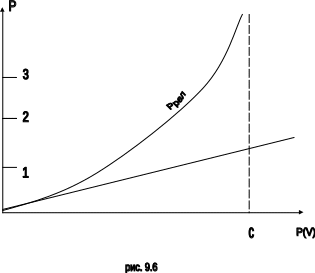 акон
сохранения импульса для системы из двух
частиц со скоростями
акон
сохранения импульса для системы из двух
частиц со скоростями
![]() и
и
![]() имеет вид:
имеет вид:
9.10 Основное уравнение релятивистской динамики
Cогласно принципу относительности Эйнштейна все законы природы должны быть инвариантны по отношению к ИСО. Т.е., математические выражения законов должны быть одни и те же во всех этих ИСО. Это относится и к законам динамики.
Однако,
основное уравнение динамики Ньютона :
![]() не удовлетворяет принципу относительности
Эйнштейна. Преобразования Лоренца при
переходе к другой ИСО придают ему иную
форму. Чтобы выполнить принцип
относительности Эйнштейна, основное
уравнение динамики должно иметь другой
вид и только при v
c
переходить в ньютоновское определение.
не удовлетворяет принципу относительности
Эйнштейна. Преобразования Лоренца при
переходе к другой ИСО придают ему иную
форму. Чтобы выполнить принцип
относительности Эйнштейна, основное
уравнение динамики должно иметь другой
вид и только при v
c
переходить в ньютоновское определение.
В
теории относительности доказано, что
этим требованиям отвечает уравнение:
![]() .
.
Оно по виду похоже на основное уравнение динамики Ньютона, однако, физический смысл здесь иной, т.к., слева стоит релятивистский импульс, если его подставить сюда, то:
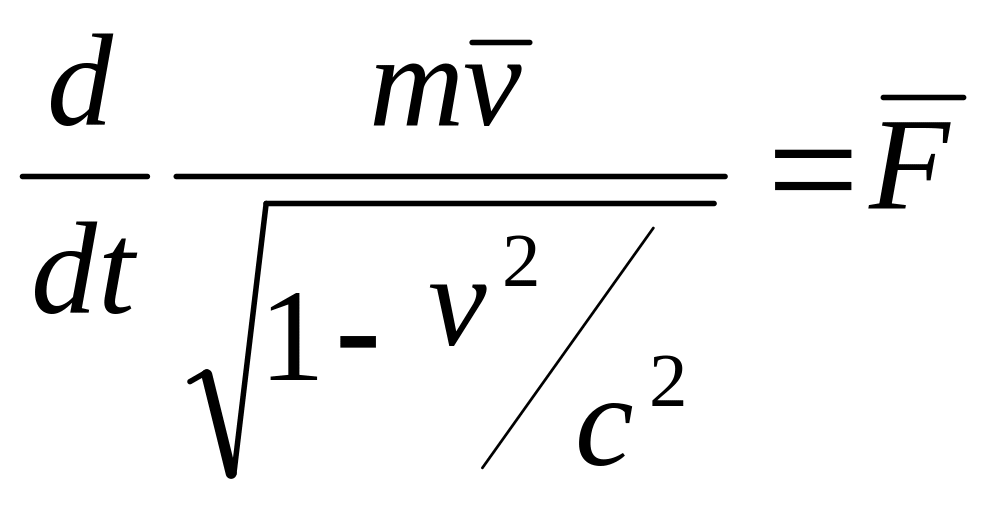 Это
есть основное уравнение релятивистской
динамики.
Это
есть основное уравнение релятивистской
динамики.
В таком виде основное уравнение динамики оказывается инвариантным по отношению к преобразованиям Лоренца и, следовательно удовлетворяет принципу относительности Эйнштейна. При переходе к другой ИСО и импульс и сила преобразуются по определенным законам, т.е., они неинвариантны.
Из
основного
уравнения релятивистской динамики
следует, что вектор ускорения частицы,
в общем случае, не совпадает с вектором
силы
![]() .
Уравнение позволяет найти вид действующей
на частицу силы, если известен вид
.
Уравнение позволяет найти вид действующей
на частицу силы, если известен вид
![]() .
С другой стороны, если известна сила и
начальные условия,
.
С другой стороны, если известна сила и
начальные условия,
![]() и
и
![]() ,
то можно найти уравнение вижения частицы
,
то можно найти уравнение вижения частицы
![]() .
.
9.11 Кинетическая энергия релятивистской частицы
Эту величину определяют также как в ньютоновской механике, как величину, приращение которой равно работе действующей на частицу силы. Найдем вначале элементарное приращение энергии на элементарном пути под действием силы:
![]() .
.
Подставив сюда выражение для силы из основного уравнения релятивистской динамики, получим:
![]() .
.
После преобразований (см. Савельев, т.1, стр.238) получим:
![]() ,
а после интегрирования:
,
а после интегрирования:
![]() .
.
По
смыслу кинетическая энергия должна
обращаться в нуль при
![]() ,
отсюда
,
отсюда
![]() .
Тогда релятивистское выражение для для
кинетической энергии частицы имеет
вид:
.
Тогда релятивистское выражение для для
кинетической энергии частицы имеет
вид:
![]() (
)
(
)
При малых скоростях выражение в скобках можно разложить в ряд:
![]() ,
тогда:
,
тогда:
![]() ,
т.е., переходит в ньютоновское определение.
,
т.е., переходит в ньютоновское определение.
9.12 Полная энергия релятивистской частицы
Кроме кинетической энергии свободная частица должна обладать дополнительной энергией равной:
![]()
Таким образом, полная энергия свободной частицы равна
![]() или
или
![]() .
.
Это следует из того, что энергия является сохраняющейся величиной, а кинетическая энергия системы частиц при столкновении не сохраняется. Невозможно удовлетворить требованию сохранения энергии во всех ИСО, если не учитывать энергию покоя в составе полной энергии.
Кроме того, из выражения для полной энергии и релятивистского импульса можно образовать инвариант, т.е., величину, не изменяющуюся при преобразованиях Лоренца. Для этого из выражений для полной энергии ( ) и импульса ( ) необходимо исключить скорость. Тогда:
![]()
Масса и скорость света с являются инвариантными величинами.
Эксперименты над быстрыми частицами подтвердили инвариантность этого выражения.
9.13 Взаимосвязь массы и энергии
Кинетическая
энергия частицы или тела есть не что
иное, как разность значений полной
энергией этой частицы (или тела) в двух
состояниях: движении со скоростью
![]() и покоя:
и покоя:
![]() .
.
Энергию
покоя свободной частицы обычно называют
ее собственной энергией:
![]() .
Эта формула справедлива как для отдельной
частицы, так и для любой системы частиц
(ядра, атомы, молекулы, твердые тела и
т.д.). Она выражает один из основных
законов теории относительности- закона
взаимосвязи массы и энергии.
.
Эта формула справедлива как для отдельной
частицы, так и для любой системы частиц
(ядра, атомы, молекулы, твердые тела и
т.д.). Она выражает один из основных
законов теории относительности- закона
взаимосвязи массы и энергии.
Энергия
покоя тела зависит от его состава и
внутреннего состояния. Например, при
нагревании тела его энергия покоя
увеличивается. Одновременно с этим
происходит возрастание массы тела, как
того требует закон взаимосвязи массы
и энергии:
![]() .
.
Закон взаимосвязи массы и энергии был надежно подтвержден в многочисленных экспериментах ядерной физики: в различных ядерных реакциях и превращениях элементарных частиц.
