11.3. Токи при размыкании и замыкании цепи

11.3.1. Токи при размыкании цепи

Поставим переключатель "П", рис. 3, в положение 1, разомкнув цепь,тогда

IR = .

Откуда (10)

Э

I

I₀

то линейное однородное дифференциальное уравнение первого порядка с разделяющимися переменными .

Решением его будет I = I , (11)

г

Рис. 4 t

де . График изменения тока при размыкании цепи

п редставлен на рис. 4.

11.3.2. Токи при замыкании цепи

Замкнем цепь (см. рис. 3), поставив переключатель "П" в полжение 2. Для нового состояния цепи имеем в соответствии с законом Ома IR = . Или

(12)

Э

I

I₀

то линейное неоднородное дифференциальное уравнение первого порядка. Решением его будет (13)

где I = , - ЭДС источника, R - сопротивление нагрузки.

Г

Рис. 5 t

рафик изменения тока при замыкании цепи, показан на рис. 5.

11.4. Энергия магнитного поля

При возрастании тока в контуре в нем возникает ЭДС самоиндукции и закон Ома за­пишется I = , где , отсюда .

Полная работа источника тока за время dt dA =

здесь I Rdt - это работа, затрачиваемая на нагревание; LI dI - это работа дополнительная к работе источника тока, обусловленная индукционными явлениями в цепи. Вся работа, совершаемая в цепи для увеличения тока от 0 до I

A = . (14)

Эта работа и будет равна энергии магнитного поля, т.е. . (15)

Для соленоида индуктивность L определяется по формуле (9), что позволяет найти

. (16)

т.к. В= . Объемная плотность энергии магнитного поля

, (17)

она измеряется в СИ в Дж /м³.

Лекция 12. Основы теории Максвелла для электромагнитного поля

В 60-х годах прошлого века (около 1860 г.) Максвелл, основываясь на идеях Фарадея, обобщил законы электростатики и электромагнетизма: теорему Гаусса - Остроградского для электростатического поля и для магнитного поля ; закон полного тока ; закон электромагнитной индукции , и в результате разработал законченную теорию электромагнитного поля.

Теория Максвелла явилась величайшим вкладом в развитие классической физики. Она позволила с единой точки зрения понять широкий крут явлений, начиная от электро­статического поля неподвижных зарядов и заканчивая электромагнитной природой света.

Математическим выражением теории Максвелла служат четыре уравнения Максвелла. которые принято записывать в двух формах: интегральной и дифференциальной. Дифференциальные уравнения получаются из интегральных с помощью двух теорем вектор ного анализа - теоремы Гаусса и теоремы Стокса. Теорема Гаусса:

(1)

(2)

- проекции вектора на оси; V - объем, ограниченный поверхностью S.

Теорема Стокса: . (3)

здесь rot - ротор вектора , который является вектором и выражается в декартовых коор­динатах следующим образом: rot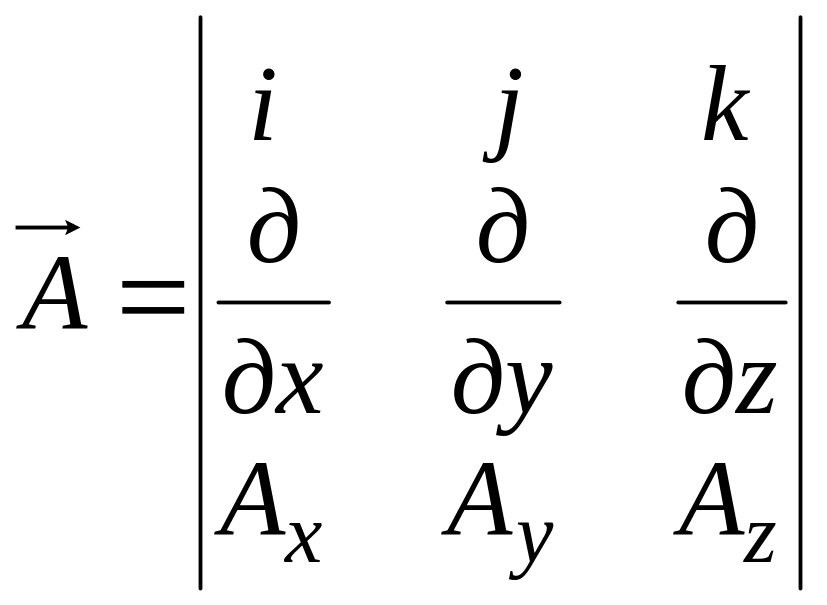 , (4)

S - площадь, ограниченная контуром L.

Уравнения Максвелла в интегральной форме выражают соотношения, справедливые для мысленно проведенных в электромагнитном поле неподвижных замкнутых контуров и поверхностей.

Уравнения Максвелла в дифференциальной форме показывают как связаны между собой характеристики электромагнитного поля и плотности зарядов и токов в каждой точке этого поля.