7.2.2. Расчет на прочность изгибаемых элементов прямоугольного поперечного сечения с одиночной арматурой

Под одиночной арматурой следует понимать всю арматуру (напряженную и ненапряженную), установленную только в растянутой от внешних нагрузок зоне изгибаемого элемента. При этом могут иметь место два расчетных случая, которые будут рассмотрены ниже.

7.2.2.1. Расчет элементов с одиночной ненапрягаемой или напрягаемой арматурой в растянутой зоне

Наиболее простой (и весьма распространенный) случай имеет место тогда, когда изгибаемый элемент не имеет предварительно напрягаемой арматуры (балки с ненапрягаемой арматурой, поперечные ребра ребристых плит и прочие).

Для рассматриваемого расчетного случая (проектируемый элемент имеет прямоугольное сечение шириной «в» и высотой «h» согласно рис.1.24)

и тогда уравнения (1.65 и 1.68) для предельного случая принимают вид:

С целью упрощения расчетов и подбора размеров поперечных сечений изгибаемых элементов нормы рекомендуют ввести безразмерные коэффициенты (α_m и ξ) в виде (с учетом 1.60):

(1.69)

откуда . (1.70)

Тогда уравнение (в) может быть преобразовано к виду

, (1.71)

где все составляющие (по нагрузкам, механическим характеристикам, размерам поперечного сечения и пр.) заданы по условиям проектирования.

Рассчитав значение (α_m) по уравнению (1.71), по формуле (1.70) определяют величину ξ. Затем по формуле (1.61) рассчитывают величину ξ_R с целью проверки условия нормальности армирования элемента.

Если окажется, что условие нормального армирования (ξ≤ξ_R) справедливо, то для определения величины A_s следует использовать уравнение (б), заменив в нем величину «х» на величину «ξh₀» согласно уравнению (1.60). То есть искомая площадь поперечного сечения арматуры в растянутой зоне элемента (А_s) может быть определена из уравнения (б) в виде:

, (1.72)

По вычисленному значению A_s производят подбор стержневой, проволочной или канатной арматуры.

Для уменьшения ширины раскрытия трещин (фактически для увеличения площади сцепления арматуры с бетоном) диаметры стержней, проволоки или канатов, согласно рекомендациям СП52-101-2003, следует принимать минимально возможными, руководствуясь технологическими требованиями по условию размещения арматуры в один ряд по ширине сечения, но не менее 12 мм для монолитных конструкций и не менее 16 мм для сборных конструкций.

Если окажется, что условие нормального армирования не соблюдается (ξ≥ξ_R), то размеры сечения при заданном классе бетона недостаточны. В этом случае необходимо повысить класс бетона на одну ступень нормированного ряда и повторить расчет. В качестве удовлетворительного выхода из создавшегося положения можно установить арматуру в сжатой от внешних нагрузок зоне изгибаемого элемента. Расчет такого элемента с двойной арматурой будет рассмотрен ниже.

Кроме сказанного, можно увеличить на один модуль (т.е. на 50 мм) высоту или ширину поперечного сечения, но эту меру применяют в последнюю очередь, поскольку это связано с изменением размеров технологической оснастки для изготовления элемента.

Заключительным видом проверки правильности расчета является проверка по минимальному проценту армирования с использованием зависимости (1.54). Если условие

A_smin<A_s , (1.73)

не выполняется, то принимают A_s=A_smin, поскольку такое значение A_s удовлетворяет и условию прочности, и условию нормального армирования, и условию минимального армирования. В заключение отметим, что при расчете элементов с ненапрягаемой арматурой в растянутой зоне следует принять

тогда формула (1.72) принимает вид

, (1.74)

где все составляющие (кроме A_sр, подлежащей определению) заданы по условиям проектирования.

После расчета A_sр дальнейшие проверки следует выполнять по такому же алгоритму, как и в случае с ненапряженной арматурой.

Расчет ведется в зависимости от высоты сжатой зоны X_R и от

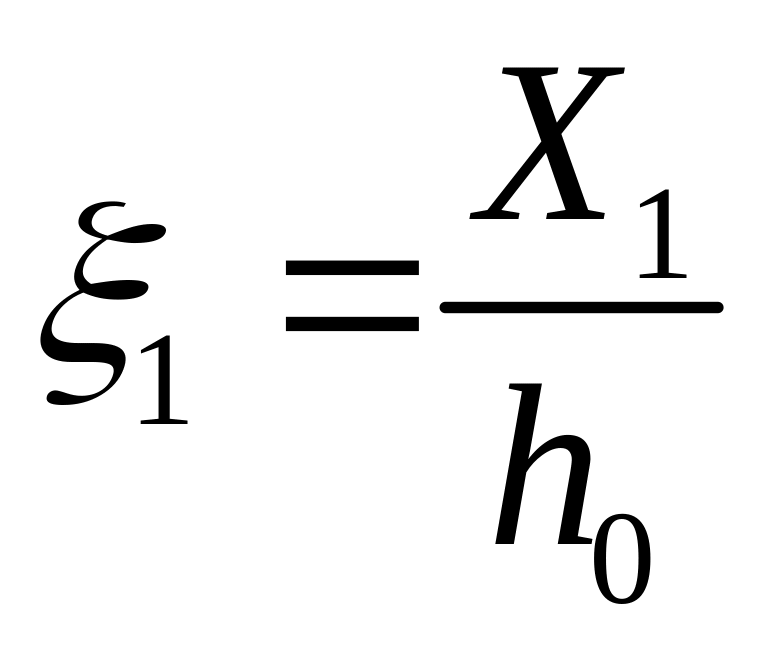
1 случай: , сечение не переармировано

2 случай: , сечение переармировано

Определение количества продольной арматуры.

Если условие выполняется, то нейтральная ось находится в пределах полки и арматура подбирается как для прямоугольного сечения b`_f = b

Если условие не выполняется, то нейтральная ось расположена в ребре, сечение рассчитывается как тавровое

Из условия можно выразить формулу для продольной арматуры.