§ 7. Характерные скорости распределения Максвелла

Найдем координаты максимума функции распределения молекул по абсолютным значениям скорости. Для этого вычислим производную функции (28) и приравняем ее к нулю. Значение коэффициента, стоящего перед экспонентой не повлияет на результат, то есть

. (29)

Вычислив производную (29), получим

, (30)

откуда находим скорость, на которую приходится максимум функции распределения молекул по скоростям, называемую наивероятнейшей скоростью:

(31)

Максимум функции распределения молекул по векторам скоростей (24) приходится на значения проекций скорости, равные нулю. Заметим, что в показателе экспоненты в функции распределения (28) стоит выражение, определяющее квадрат наивероятной скорости, и запишем функцию распределения молекул по модулям скорости в виде:

, (32)

а вероятность для частицы иметь скорость в интервале равна

(33)

Выполним в (33) замену переменной. Введем новую переменную  - относительную скорость молекулы - и получим выражение для нахождения вероятности обнаружения у частицы относительной скорости в интервале :

. (34)

Следовательно, функция распределения молекул по значениям относительной скорости Максвелла имеет вид

. (35)

В функцию распределения по относительным скоростям не входит ни одной характеристики отдельной молекулы, максимум этой функции приходится, очевидно на u=1. Таким образом, функция распределения (35) справедлива для любого идеального газа, находящегося в термодинамическом равновесии, то есть является универсальной зависимостью.

Функция распределения ‑ конечный результат описания вероятностной закономерности. Полученные выше функции распределения характеризуют систему в состоянии термодинамического равновесия, поэтому не зависят от времени, ни явно, ни неявно. Используя функции распределения, можно вычислять средние значения параметров состояния системы, которые, естественно могут быть определены и экспериментально.

Как тестовую задачу для метода, основанного на использовании функции распределения, рассмотрим вычисление среднего квадрата скорости молекул равновесного газа. Ответ этой задачи нам уже известен и получен, исходя из основного уравнения молекулярно-кинетической теории и определения температуры.

Итак, средний квадрат скорости равен интегралу от нуля до бесконечности от произведения квадрата скорости на функцию распределения:

. (36)

Интегрирование по частям последнего интеграла дает выражение для среднего квадрата скорости в виде

, (37)

что находится в полном соответствии с выражением для средней квадратичной скорости, полученным из основного уравнения МКТ.

Определим теперь по общему правилу нахождения средних значений выражение для средней скорости движения молекул идеального газа в состоянии термодинамического равновесия.

. (38)

Для вычисления интеграла выполним замену переменной b  v² тогда получим:

(39)

после интегрирования по частям и тождественных преобразований получаем

. (40)

Таким образом, можно показать характерные скорости функции распределения Максвелла молекул по абсолютным значениям скорости, что представлено на рис. 1.7.1.

С

Рис. 1.7.1. Характерные скорости функции распределения молекул Максвелла по абсолютным значениям скорости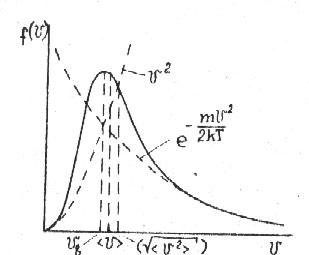

редняя скорость и средний квадрат скорости молекул больше наивероятнейшей скорости. Это ясно из того, что функция распределения несимметрична, причем площадь под графиком функции распределения Максвелла слева от максимума меньше площади под графиком справа от максимума. Это означает, что доля молекул, имеющих скорости большие наивероятнейшей превосходит долю молекул, скорости которых меньше нее, а следовательно и средняя, и средняя квадратичная скорости больше наивероятнейшей.

По описанной выше схеме можно найти выражения для средней относительной скорости, среднего квадрата относительной скорости, используя функцию распределения молекул по относительным скоростям (34). А так же определить вычисления средних значений квадрата скорости, относительной скорости, квадрата относительной скорости, кинетической энергии.

Экспериментальная проверка распределения молекул по абсолютным значениям скорости.

Первое экспериментальное исследование скоростей молекул было осуществлено О. Штерном в 1950 г. Прибор, использованный для этой цели, состоял из двух коаксиальных цилиндров (рис.___).

П

Рис. ___ . Экспериментальное исследование распределения молекул газа по скоростям.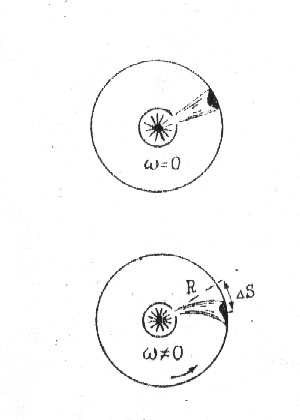

о оси прибора была н атянута платиновая нить; электрическим током с ее поверхности испарялись атомы серебра. Покинув нить, атомы серебра двигались по радиальным направлениям. Чтобы атомы серебра не отклонялись за счет соударения с молекулами воздуха, прибор поместили в вакуум. Внутренний цилиндр имел узкую щель, проходя через которую пучок атомов серебра попадал на внутреннюю поверхность второго цилиндра. Чтобы можно было говорить о том, что молекулы серебра, вылетающие из щели, характеризуют состояние молекул газа во внутреннем цилиндре (т.е., например, температура этого газа равна температуре нити), требуется выполнение соотношения , где – время свободного пробега (длина свободного пробега), – время пролета вблизи отверстия (d – ширина щели). Если это условие реализуется (т.е. d<< ), то говорят об эффузии газа.

Если цилиндры неподвижны, то на внутренней поверхности внешнего цилиндра получается узкая полоса серебра (рис.__).

Если же цилиндры привести во вращение (с угловой скоростью ), то положение следа сместится на расстояние , где . Отсюда следует что зная , можно найти . Если бы все атомы серебра имели одинаковую скорость, то след бы представлял собой узкую полоску. На самом же деле имеет место размытая полоса. Исследуя зависимость толщены следа от , можно оценить зависимость числа осажденных атомов серебра от скорости этих атомов. Эксперимент качественно согласуется с теоретическим прогнозом (хорошо согласуется с теорией экспериментальная оценка средней скорости атомов).

Более точно закон распределения Максвелла был проверен Ламмертом (1929г.), который использовал эффузные пучки и селектор скорости. В его опыте молекулярный пучок пропускался через два вращающихся диска с радиальными щелями, смещенными друг относительно друга (селектор скорости). Через второй диск пролетали только те атомы, которые подлетали в тот момент, когда на пути пучка вставала прорезь второго диска. Таким образом, это устройство позволяло выделить из пучка молекулы, обладающие определённым значением скорости ( , но ). Исследовалась величина в зависимости от вариации . Установлено полное согласие теории с экспериментальными данными. Следует подчеркнуть, что в опыте Ламмерта непосредственно исследовалась зависимость , т.к. количество молекул, пролетающих через отверстие в единицу времени, пропорционально и скорости молекулы.