2. Основы молекулярной физики и термодинамики

1. Основные формулы Количество вещества

,

где – число частиц (атомов, молекул, ионов); – постоянная Авогадро.

Молярная масса вещества

,

где – масса однородного тела; – количество вещества этого тела.

Уравнение Менделеева-Клапейрона (уравнение состояния идеального газа)

,

где m – масса газа, M – молярная масса газа, R – молярная газовая постоянная, – количество вещества, T – термодинамическая температура.

Опытные газовые законы:

а) изотермический процесс (закон Бойля-Мариотта, T=const, m=const):

pV=const

б) изобарный процесс (закон Гей-Люссака, p=const, m=const):

в) изохорный процесс (закон Шарля, V=const, m=const):

г) объединенный газовый закон (m=const):

.

Основное уравнение кинетической теории газов

,

где m₀ – масса одной молекулы, n – концентрация молекул, – средняя квадратичная скорость.

Средняя кинетическая энергия поступательного движения молекулы

,

где k – постоянная Больцмана.

Средняя полная кинетическая энергия молекулы

,

где i – число степеней свободы молекулы.

Зависимость давления газа от концентрации молекул и температуры:

p=nkT.

Скорости молекул:

– средняя квадратичная;

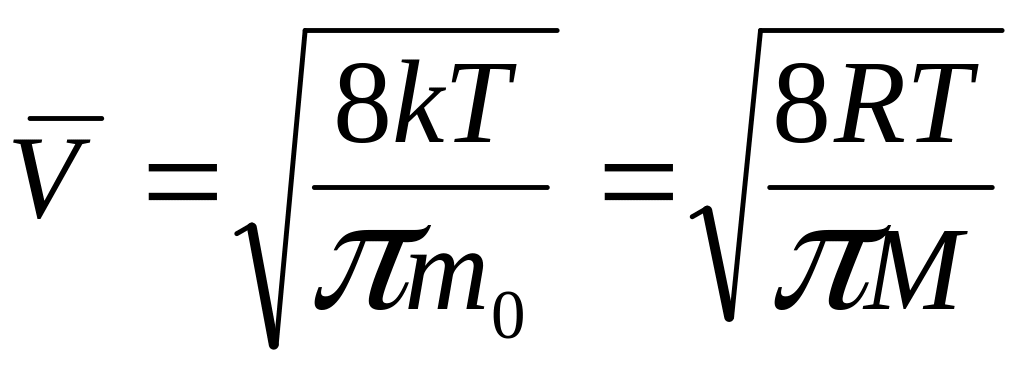– средняя арифметическая;

– наиболее вероятная,

где m₀ – масса одной молекулы.

Удельные теплоемкости газа при постоянном объеме (с_v) и постоянном давлении (с_p)

, .

Связь между удельной c и молярной C теплоемкостями

, .

Уравнение Майера:

.

Внутренняя энергия идеального газа

.

Первое начало термодинамики

,

где Q – теплота, сообщенная системе (газу); U – изменение внутренней энергии системы; A – работа, совершенная системой против внешних сил.

Работа расширения газа: в общем случае;

при изобарном процессе;

при изотермическом процессе;

или 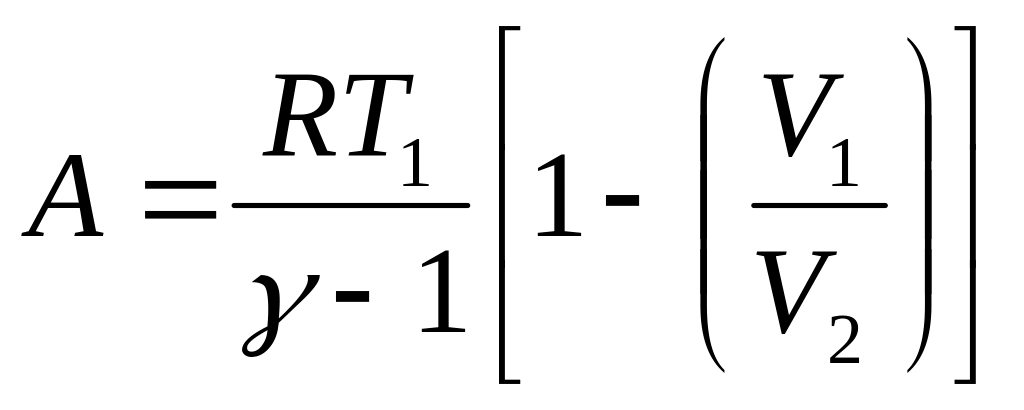при адиабатном процессе, где – показатель адиабаты.

Уравнение Пуассона, связывающие параметры идеального газа при адиабатном процессе:

, , ,

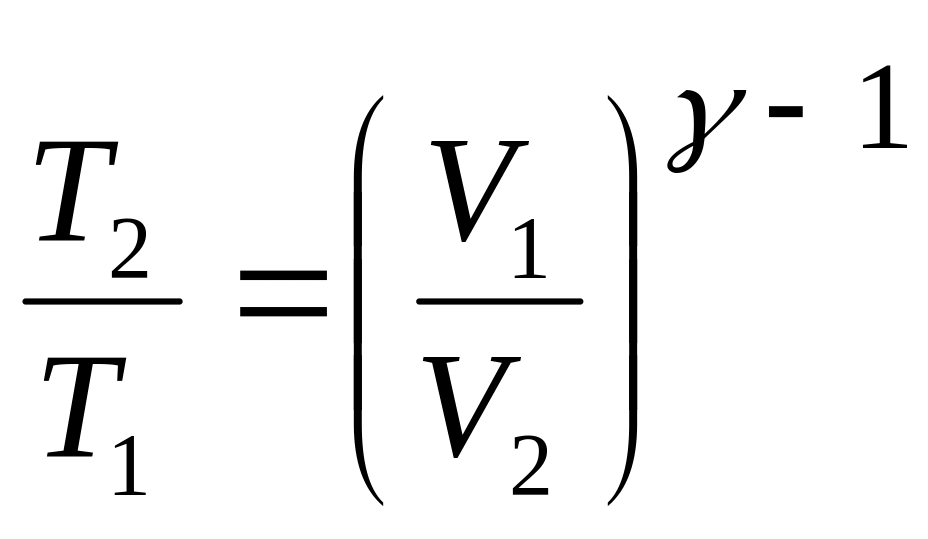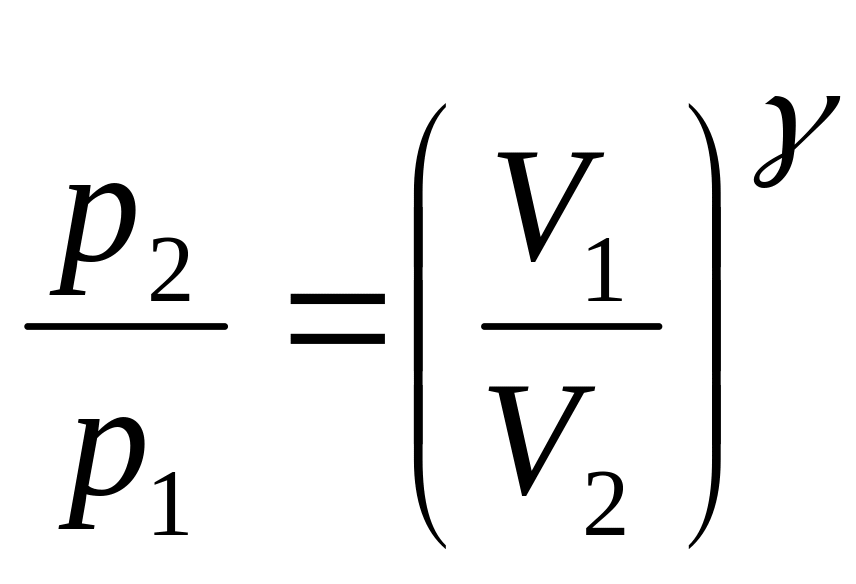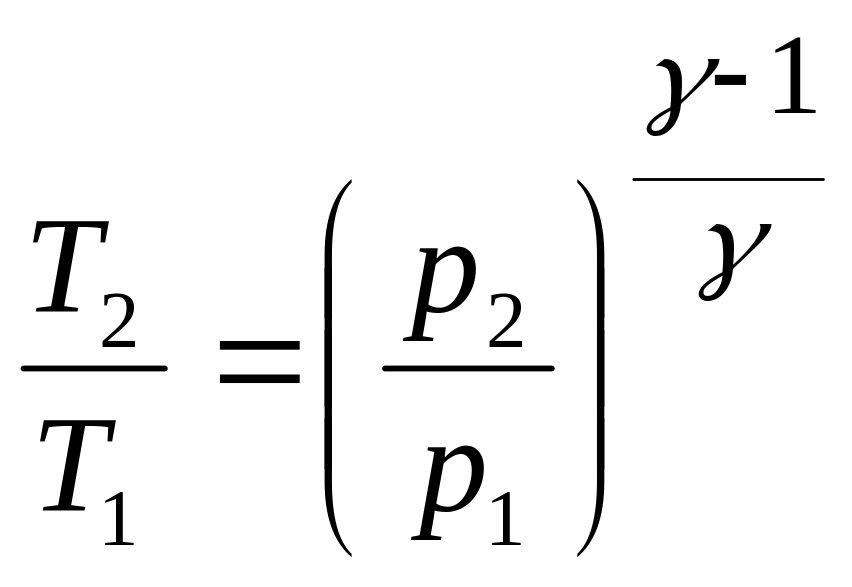
Коэффициент полезного действия (к.п.д.) тепловой машины:

Термический к.п.д. цикла

,

где – теплота, полученная рабочим телом от теплоотдатчика;

–теплота, переданная рабочим телом теплоприемнику.

Термический к.П.Д. Цикла Карно

,

где и – термодинамические температуры теплоотдатчика и теплоприемника.

2.2. Примеры решения задач.

Пример 1. Азот массой m =0,1 кг был изобарически нагрет от температуры = 200 К до температуры = 400 К. Определить работу А, совершенную газом, полученную им теплоту и изменение внутренней энергии азота.

Дано:

m = 0,1 кг

= 200 К

= 400 К

A = ?, Q = ?,

=?

Р ешение:

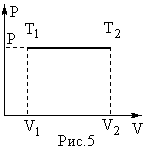
Изобразим процесс на PV – диаграмме (рис.5).

Работа газа при изобарическом расширении

.

Из уравнения Менделеева - Клапейрона:

, ,

поэтому: .

Размерность:

.

Изменение внутренней энергии газа определяется изменением его температуры:

,

где: – молярная теплоемкость газа при постоянном объеме, i – число степеней свободы молекулы (азот –двухатомный газ, поэтому i = 5). Тогда:

11

.

Размерность: .

На основании первого начала термодинамики определим теплоту, полученную газом:

.

Размерность: .

Ответ: A = 5,9· Дж, = 14,8· Дж, Q = 20,7· Дж.

Пример 2. В сосуде находится водород массой m = 10 г. При изотермическом расширении объем водорода увеличивается в два раза. Считая водород идеальным газом, найти приращение его энтропии.

Дано:

m = 10 г = кг

Решение:

Согласно второму началу термодинамики изменение энтропии определяется начальным и конечным состоянием системы. Если процесс перехода системы из начального состояния в конечное обратимый, то:

.

По первому началу термодинамики:

.

При изотермическом процессе (T = const) изменение внутренней энергии равно нулю (dU = 0), поэтому:

,

,

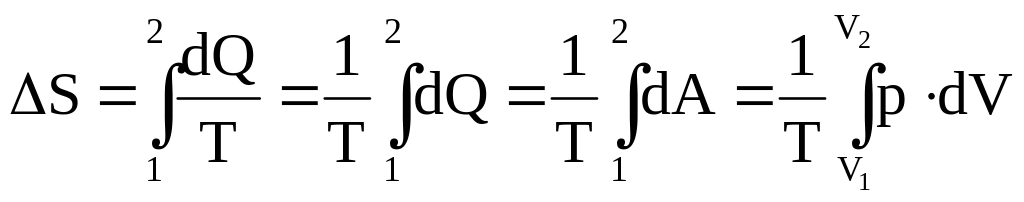Из уравнения Менделеева - Клапейрона: ,

12

,

.

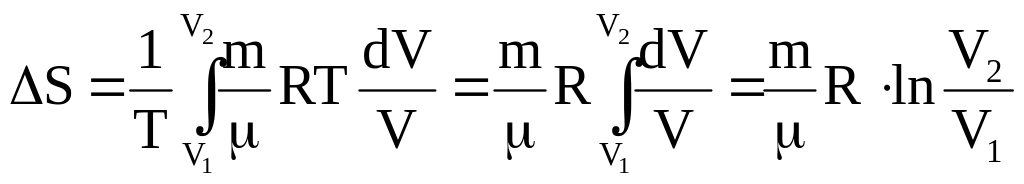Размерность: .

Ответ: .

Пример 3. Один моль идеального газа с показателем адиабаты γ совершает политропический процесс, в результате которого абсолютная температура газа Т возрастает в η раз. Показатель политропы равен n. Найти приращение энтропии газа ΔS.

Дано:

γ, n

ΔS = ?

Решение.

Приращение энтропии при обратимом процессе:

,

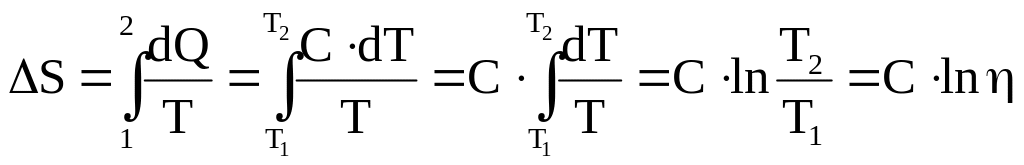где: С – молярная теплоемкость идеального газа в этом процессе.

Политропический процесс описывается уравнением:

,

где: n – показатель политропы, p – давление газа, V – объем, занимаемый газом.

Определим С из выражения для показателя политропы:

,

где: , – молярные теплоемкости при постоянном давлении и постоянном объеме соответственно. Тогда :

,

отсюда:

.

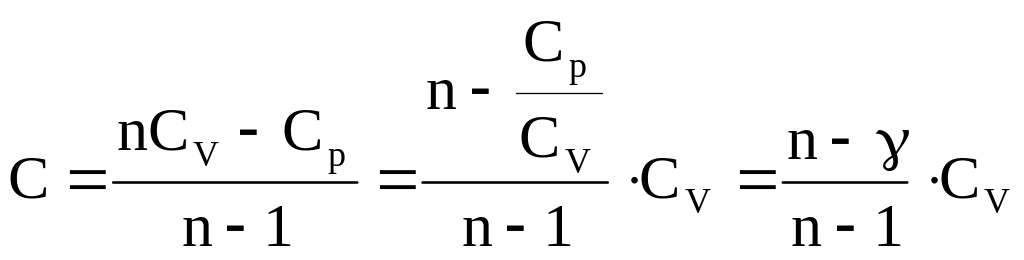Так как и , то

,

где: i – число степеней свободы,

R — универсальная газовая постоянная.

Определим i:

.

Тогда:

.

Следовательно, молярная теплоемкость С идеального газа в этом процессе:

.

Приращение энтропии:

.

Размерность: .

Ответ: .