52

Кинематика, глава 1. Кинематика точки 02.03.09, 17.01.2010, 10.03.10

§5. Задание движения материальной точки в криволинейных координатах.

1º. Понятие криволинейных (обобщенных) координат точки.

Определение 1.

Криволинейными или, иначе, обобщенными координатами материальной точки будем называть три независимые величины ,  ,  , которые обладают следующими свойствами.

1. Для любых значений ,  ,  из некоторой области 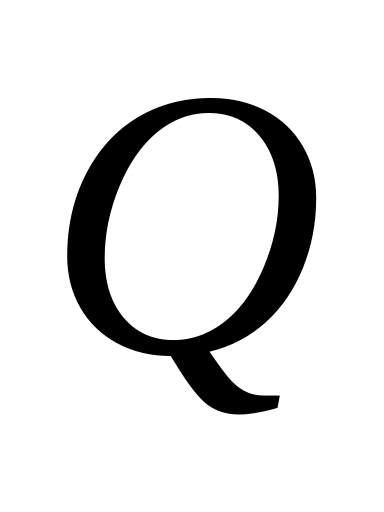 трехмерного пространства переменных ,  ,  определена однозначная, дважды непрерывно дифференцируемая вектор-функция , такая, что ее векторное значение

= (1)

задает положение материальной точки в абсолютном пространстве при .

2. Для любого положения материальной точки в абсолютном пространстве можно поставить в соответствие одно и только одно значение переменных ,  ,  .

3. При любых значениях ,  ,  из области  смешанное произведение векторов ,  ,  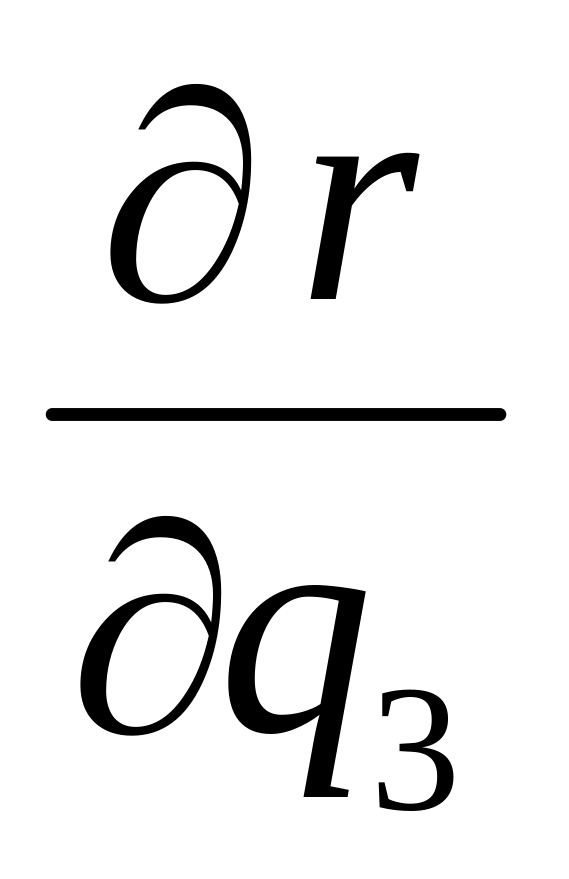не равно нулю, т.е.

, , . (2)

Если задана система отсчета  , то в скалярной форме соотношение (1) можно записать в виде

= , = , = . (3)

Из сформулированных выше свойств вытекает, что

• функции , , однозначны и дважды непрерывно дифференцируемы;

• система (3) разрешима относительно обобщенных координат ,  ,  , так что

= , = , = .

Разрешимость следует из теоремы о неявной функции, поскольку якобиан правой части системы (3) отличен от нуля при всех из области  . Действительно, матрица Якоби для системы (3) имеет вид:

.

Ее определитель совпадает с левой частью неравенства (2). А потому . Данное неравенство выполняется в любой точке из области  . Поэтому из определения 1 обобщенных координат ,  ,  следует, что справедливы условия теоремы о неявных функциях для системы уравнений (3), а из самой теоремы вытекает существование решений ,  ,  этой системы.

Замечания.

1. На практике иногда удается указать переменные ,  ,  , которые удовлетворяют описанным условиям не для любой точки абсолютного пространства, а лишь для некоторого множества из него. Если по предварительным прогнозам из каких-либо соображений известно, что на изучаемых моделях движения материальная точка не покинет указанное множество, то переменные ,  ,  могут быть приняты за обобщенные координаты для описания и исследования таких движений.

2. Если отсутствуют криволинейные координаты ,  ,  , для которых справедливы сформулированные выше свойства во всем абсолютном пространстве, то можно вводить криволинейные координаты ,  ,  для части пространства, в которой эти условия выполняются.

Для оставшейся части пространства можно подобрать другие переменные ,  ,  так, чтобы для них выполнялись указанные условия. Причем новые переменные ,  ,  вводятся так, чтобы не нарушались условия из определения криволинейных координат и в некоторой части пространства, где они справедливы и для переменных ,  ,  .

Общая часть пространства для переменных ,  ,  и ,  ,  позволяет при изучении движений осуществлять переход от криволинейных координат ,  ,  к криволинейным координатам ,  ,  , как только материальная точка окажется в этой общей части пространства.

Пример 1. Цилиндрическая система координат.

( )

( )

( )

Рис. 1.

Положение точки  задается переменными ,  ,  (см. рис.1), где — расстояние от полюса  до проекции точки  на плоскость  ; ; — угол в плоскости  , отсчитываемый от положительного направления оси  до луча  ( — это проекция точки  на плоскость  ); ; положительное направление отсчета угла  задается правилом правой руки; — проекция радиус-вектора точки  на ось  ; ( , — проекция точки  на ось  ); .

Связь декартовых прямоугольных координат ,  ,  точки  с цилиндрическими задается следующими формулами:

= , = , = .

Обратная зависимость ,  ,  от ,  ,  , т.е. связь цилиндрических координат с декартовыми, имеет вид:

= , , = .

Если , то аналогичным образом можно ввести цилиндрические координаты ,  ,  по отношению к системе координат , у которой, например, полюс смещен вдоль оси , ось совпадает с осью , а оси и коллинеарны осям и .

В тех случаях, когда движения точки могут приводить ее на ось  , следует переходить к описанию этих движений в переменных ,  ,  .

Пример 2. Сферическая система координат.

Положение точки  задается криволинейными координатами ,  ,  (см. рис.2). Они имеют следующий геометрический смысл.

Координата обозначает расстояние от полюса  декартовой прямоугольной системы координат до точки  . Она может принимать значения .

Координата обозначает угол в плоскости  , отсчитываемый от положительного направления оси  до проекции  вектора на плоскость  . Она может изменяться в диапазоне . Положительное направление отсчета угла задается правилом правой руки относительно орта  .

( )

Рис. 2.

Координата определяется значением угла между плоскостью  и радиус-вектором точки  . Угол  отсчитывается от плоскости  до радиус-вектора и может изменяться в диапазоне . Он принимает значение , если точка  находится на положительной полуоси  ; , если  находится на отрицательной полуоси , и , если  находится в плоскости  .

Угол  положителен, если точка  принадлежит положительному полупространству относительно плоскости  ; угол  отрицателен, если  находится в отрицательном полупространстве относительно плоскости .

На рисунке 2 точка  обозначает ортогональную проекцию точки  на плоскость  , а — ортогональную проекцию точки  на ось  .

Связь декартовых прямоугольных координат ,  ,  точки  со сферическими задается формулами:

, , .

Обратная зависимость, т.е. связь сферических координат с декартовыми, имеет вид:

, , .

Угол  не определен, если точка  находится на оси  . Угол  не определен, если точка  совпадает с точкой отсчета  .