5.4. Хвильове рівняння

Згідно з рівняннями (5.4) і (5.5) змінне з часом електричне поле породжує змінне магнітне поле. Це змінне магнітне поле породжує змінне електричне поле і т.д. Таким чином, якщо збудити змінне електричне або магнітне поле, в навколишньому середовищі виникає послідовність взаємних перетворень електричного і магнітного полів, які поширюються від точки до точки. Цей процес буде періодичним в часі і в просторі і, отже, являє собою хвилю. Висновок про можливість існування електромагнітних хвиль випливає із рівнянь Максвелла.

Запишемо рівняння Максвелла для однорідного (ε=const, μ=const) електронейтрального (ρ=0) непровідного (j=0) середовища. В цьому випадку

Отже, рівняння (5.19)—(5.22) набирають вигляду

(5.23)

(5.24)

(5.25)

(5.26)

Застосуємо до рівняння (5.23) операцію rot

(5.27)

Оскільки середовище є однорідним, то, змінивши порядок диференціювання за координатами та часом у правій частині рівняння (5.27) і враховуючи рівняння (5.24), отримаємо

(5.28)

Скориставшись правилом подвійного векторного добутку = — і зважаючи на те, що оператор має стояти перед функцією, на яку він діє, знаходимо

оскільки, згідно з (5.25) =0.

Враховуючи останнє співвідношення та (5.28), маємо

(5.29)

Тут — оператор Лапласа (лапласіан) [10].

Розпишемо у рівнянні (5.29):

(5.30)

Подібним чином рівнянню (5.24) можна надати вигляду

(5.31)

(5.32)

Зазначимо, що рівняння (5.29) і (5.31), а отже (5.30) і (5.32), нерозривно зв’язані між собою, оскільки вони отримані з рівнянь (5.23) і (5.24), кожне з яких вміщує і , і .

Рівняння вигляду

є хвильовим рівнянням (див. [11]). Будь-яка функція, що задовольняє такому рівнянню, описує деяку хвилю, причому корінь квадратний із величини, оберненої коефіцієнту при , дає фазову швидкість цієї хвилі. Отже, рівняння (5.30) та (5.32) є хвильовими і вказують на те, що електромагнітні поля можуть існувати у вигляді електромагнітних хвиль, фазова швидкість яких

(5.33)

Для вакууму і за формулою (5.33) швидкість електромагнітної хвилі

Обчислення і перевірку розмірностей пропонується читачеві виконати самостійно.

Таким чином, у вакуумі фазова швидкість електромагнітних хвиль співпадає зі швидкістю світла, а в середовищі

5.5 Плоска електромагнітна хвиля

Дослідимо плоску електромагнітну хвилю, що розповсюджується в однорідному непровідному середовищі ( і — сталі). Направимо вісь х перпендикулярно до хвильових поверхонь. Тоді і , а також їх складові не будуть залежати від координат у і z. Тому рівняння (5.15) – (5.18) спрощуються таким чином:

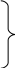
(5.34)

(5.35)

(5.36)

(5.37)

Перше з рівнянь (5.34) і рівняння (5.37) показують, що Ех не може залежати ні від t, ні від х. Перше з рівнянь (5.35) і рівняння (5.36) дають такий самий результат для Нх. Інші рівняння систем (5.34) і (5.35) свідчать про зміну векторів і у напрямках у і z.

Отже, поле електромагнітної хвилі не має складових вподовж осі х, тобто вектори і перпендикулярні до напрямку поширення хвилі – електромагнітні хвилі є поперечними.

При поширенні хвилі в напрямку х рівняння (5.30) і (5.32) у проекціях на координатні осі набирають вигляду

(5.38)

(5.39)

де — фазова швидкість хвилі.

Найпростішими рішеннями рівнянь (5.38) і (5.39) будуть рівняння

(5.40)

(5.41)

де k – хвильове число, що дорівнює і — початкові фази коливань в точках з координатою х=0, Н_о і Е_о — амплітудні значення змінних Н і Е.

Сумісний аналіз рівнянь (5.40) і (5.41) з системами (5.34) і (5.35) приводить до висновку, що фази коливань векторів і однакові (тобто = ), а співвідношення між амплітудами коливань виражається формулою:

Помноживши рівняння (5.40) і (5.41) на орти відповідних осей, отримаємо рівняння плоскої електромагнітної хвилі у векторній формі:

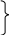
(5.42)

Н а рис. 5.3 показано „миттєва фотографія” плоскої електромагнітної хвилі з початковою фазою α=0.

За довільного напрямку поширення хвилі рівняння (5.42) матимуть вигляд:

Рис.5.3