
- •2)Аналітичне оцінювання методів визначення ефект застос комун-й.
- •3) Ануїтет. Майбутня вартість унуїтету
- •4) Багатопланові аналітичні методи
- •5) .Визначення ефективних категорій рекламо носіїв
- •7) Визначення стандартних відхилень розподілів імовірностей грошових надходжень інвестиційних проектів
- •8) Визначення управлінських рішень та їх ознаки
- •9) Визначення ціни ліцензії
- •11) Використання формули Ансоффа при оцінці інтелектуальної продукції
- •12) Використання формул Кіфера для оінки окремих факторів невизначеності
- •13). Використання формули Ольсена при оцінці інтелектуальної продукції, її модифікації
- •14) Витрати на тисячу переглядів та витрати на рейтинг при визначенні ефективності витрат на комунікації
- •15). Відбір критеріїв для планування нддкр
- •16) Внутрішня ставка прибутковості та її модифікована величина при обґрунтуванні доцільності інвестиційного проекту. Її переваги та недоліки
- •17) Дисконтування його суть
- •18) Ділові ігри як метод обґрунтування рішень
- •19) Евристичні моделі обґрунтування та прийняття рішень
- •16. Економіко-математичні моделі при оцінці комунікацій
- •20) Економічна оцінка інноваційного продукту
- •21) Експериментальна перевірка використання методу регресивно-кореляційного аналізу для оцінки економічної ефективності комунікацій.
- •22) Завдання визначення ефективності застосування комунікацій.
- •23) Загальні чинники ефективності комунікацій.
- •24) Інтелектуальна продукція, її специфіка та проблеми оцінки.
- •25) Класифікація інновацій.
- •26) Класифікація ризику.Абсолютні та відносні міри ризику.
- •27) Класифікація управл.Рішень
- •28) Концепція вартості грошей у часі
- •29) Концепція формування інвестиційних рішень
- •30) Маржинальний прибуток та його сутність
- •32) Математ.Методи в ек.Аналізі
- •33) Методи індексу прибутковості. При визначенні доцільності інвестиційного проекту
- •34) Метод періоду окупності при обгрунтувані доцільності інвестування. Переваги та недоліки
- •35) Метод чистої теперешньої вартості інвестиційного проекту. Переваги та недоліки
- •36) Методи групової роботи
- •40) Обєкти інтелектуальної власності к-я.
- •42) Основні етапи підготовки управлінського рішення.
- •46) Принципи інвестиційного менеджменту.
- •47) Проблеми оцінки економ ефективності інновацій.
- •48) Прості проценти
- •50) Регресійно-кореляційний аналіз при оцінці екон-ї ефект-ті комунікацій.
- •51) Ризик, його сутність та визначення.
- •52) Середня ставка прибутковості інвестицій. Її переваги та недоліки.
- •53) Складні проценти
- •54) Сукупність переглядів при визначенні ефективності комунікацій.
- •55) Сумарні рейтинги переглядів при визначенні ефект-ті комунікацій.
- •56) Сутність економічного аналізу.
- •57) Сутність методу еквівалентної певності при оцінці ризику
- •58) Сутність методу ставки дисконту з урахуванням ризику
- •59) Сутність, визначення, характеристика інновацій.
- •61) Теперішня в-сть ануїтету. Перпетуїтет
- •62) Тестування при оцінюванні ефективності комунікацій
- •63) Традиційні методи ек аналізу
- •64) Цілі визначення ефективності застосування комунікації.
- •66) Частота переглядів при визначенні ефективності витрат на комунікації.
48) Прості проценти
Простим процентом називається нарахування з теперішньої вартості вкладу в кінці одного періоду платежу, зумовленого умовами інвестування (місяць, квартал тощо).
Простий процент обчислюється за такою формулою (1.1): I = Pіt, (1.1)
де I — величина прибутку власника інвестицій;
i — процентна ставка;
t — період часу інвестування;
P — первісна сума інвестиції (вкладу).
Сутність методу нарахування за простими процентами зводиться до того, що проценти нараховуються впродовж усього терміну інвестицій (кредиту) на ту саму величину капіталу, що інвестується. Наприкінці періоду t сума, одержувана інвестором, дорівнює P + I. Тоді:
S = P + I = P + Pit = P(1 + it). (1.2)
Величина (1 + it) зветься множником нарощування простих процентів.
При використанні простих процентів, коли термін угоди не дорівнює цілому числу років, період нарахування процентів виражається дробовим числом, тобто як відношення числа днів функціонування угоди до числа днів у році (1.3):
t=n/K, (1.3)
де n — число днів функціонування угоди;
К — часова база (кількість днів у році).
В цьому разі формула (1.2) набуде такого вигляду:
S=1+i*n/K (1.4)
В ряді країн для зручності обчислень рік триває 360 днів. Це так звана «німецька практика». Проценти, що розраховані за часовою базою K = 360 днів, називаються звичайними чи комерційними.
Існує також «французька практика», коли тривалість року К = 360 днів, а тривалість місяців за днями відповідає календарному обчисленню. І, нарешті, в цілій низці країн використовується «англійська практика», що враховує тривалість року К = 365 днів, а тривалість місяців року — згідно з календарним обчисленням.
При математичному дисконтуванні розв’язується задача, зворотна визначенню нарощуваної суми. Сформулюємо її таким чином: яку суму необхідно інвестувати на t років, щоб при нарахуванні на неї процентів за ставкою і отримати суму, що дорівнює S.
Використовуючи формулу (1.2) розрахунку нарощуваної суми за простою процентною ставкою, отримаємо: P=S*1 / (1 + it)
де знаменник 1 / (1 + it) — дисконтний множник, що показує, в скільки разів первісна сума є меншою від нарощеної.
50) Регресійно-кореляційний аналіз при оцінці екон-ї ефект-ті комунікацій.
Зв'язок між факторами соц-ек явищ та ефект-тю комунікацій має причинно-наслідк хар-р. Ознаки, які хар-ють причини та умови зв’язку наз факторними (х), а ті, які хар-ть наслідки зв’язку – результативними (у).
Між ознаками х і у виникають різні за природою і хар-ром зв’язки, зокрема функціональні і стохаст.
При функц зв’язку кожному значенню х відповідає одне чітко визначене значення у.
При стохаст зв’язку кожному знач х відповідає певна множина значень у, які утворюють умовний розподіл.
Якщо
замінити умовний розподіл середньою
величиною
 ,
то утвориться різновид стохаст зв’язку
– кореляційний.
,
то утвориться різновид стохаст зв’язку
– кореляційний.
У
вип кореляційного зв’язку кожному
значенню ознаки х відповідає середнє
значення результативної ознаки
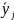 .
.
Оцінка щільності зв’язку грунт на правильності складання дисперсій.
У моделі аналітичного групування мірою щільності зв’язку є відношення міжгрупової дисперсії до загальної, яке наз кореляційним відношенням.
Загальна дисперсія вимірює варіацію результ ознаки у , тобто результат госп дія-ть підпр-ва, обумовлений впливом всіх можливих чинників впровадження комунікації по одному, а міжгрупова дисперсія вимірює варіацію рез ознаки у за рах впливу тільки групової ознаки х.
Кореляц відношення щільності зв’язку визнач за ф-лою:

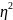 -
кореляційне відношення
-
кореляційне відношення
 -
міжгрупова дисперсія
-
міжгрупова дисперсія
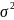 – загальна
дисперсія
– загальна
дисперсія
Кореляц відношення може коливатись від 0 (за умови відсутності зв’язку) до 1 (за умови функціонального зв’язку). Чим більше корел відношення наближ до 1, тим щільнішим є зв'язок.
Оск щільний зв'язок може виникн випадково, необх перевір його істотність, тобто довести невипадковість зв’язку:
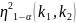
α – певний рівень істотності
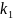 -
перше число ступенів свободи
-
перше число ступенів свободи

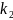 -
друг число ступенів свободи
-
друг число ступенів свободи
 ]
]
m – число груп
n – обсяг сукупності (вибірки)
Якщо > , то зв'язок визнеється істотним.
У моделі регресивного аналізу хар-кою кореляц звязку є теоретична лінія регресії, яка опис ф-єю: y=f(x) (у заг вигляді), частіше – лінійним рівнянням: y=a+bx.
При аналізі залежності показників госп дія-ть від показників застосування комунікацій складові формули мають такий екон зміст:
- коеф регресії показує на скільки зміняться показники госп дія-ті при зміні показників показників застосування комунікацій у кількісному виразі на одиницю;
- початковий рівень регресії показує яким би був рівень аналізованого показника госп дія-ті за відсутності застосування комунікації.
