13) Линейное неоднородное уравнение второго порядка с постоянными коэффициентами

Общее решение неоднородного уравнения есть сумма общего решения однородного уравнения   и некоторого частного решения   неоднородного.

14) Уравнения в полных дифференциалах. Интегрирующий множитель.

Уравнение

                                                                                                                           (1)

называется уравнением в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функции  , т.е.

.

Теорема. Для того, чтобы уравнение (1) являлось уравнением в полных дифференциалах, необходимо и достаточно, чтобы в некоторой односвязной области   изменения переменных   и   выполнялось условие

(2)

Общий интеграл уравнения (1) имеет вид 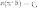  или

15) Ифференциальные уравнения высших порядков

3.1. Основные понятия

Дифференциальные уравнения порядка выше первого называются ДУ высших порядков. ДУ второго порядка в общем случае записывается в виде

или, если это возможно, в виде, разрешенном относительно старшей производной:

16) Числовой ряд — это числовая последовательность, рассматриваемая вместе с другой последовательностью, которая называется последовательностью частичных сумм (ряда).

Пусть   — числовая последовательность; рассмотрим наравне с данной последовательностью последовательность

каждый элемент которой представляет собой сумму некоторых членов исходной последовательности. В наиболее простом случае используются обычные частичные суммы вида

Вообще, для обозначения ряда используется символ

поскольку здесь указана исходная последовательность элементов ряда, а также правило суммирования.

В соответствии с этим говорится о сходимости числового ряда:

• числовой ряд сходится, если сходится последовательность его частичных сумм;

• числовой ряд расходится, если расходится последовательность его частичных сумм:

• числовой ряд сходится абсолютно, если сходится ряд из модулей его членов.

Если числовой ряд сходится, то предел S последовательности его частичных сумм носит название суммы ряда:

17) Признаки сходимости и расходимости рядов с неотрицательными членами.

Ряд с неотрицательными членами сходится тогда и только тогда, когда последовательность частичных сумм ограничена сверху.

18)Признак сравнения рядов с положительными членами. Пусть даны два ряда с неотрицательными членами   a_n и  b_n. Если существует натуральное число N такое, что неравенство a_n ≤ b_n выполнено для всех n ≥ N, то из сходимости ряда   b_n следует сходимость ряда   a_n, а из расходимости ряда   a_n -расходимость ряда   b_n.

19) Признак Коши.

а) Если существует натуральное число N такое, что для числовой последовательности { }, построенной из членов ряда   a_n, a_n ≥ 0, для всех n ≥ N выполняется неравенство   ≤ q < 1 (q — фиксированное число, не зависящее отn), то ряд сходится; если для всех n ≥ N выполняется неравенство   ≥ 1, то ряд расходится.

б) Если у последовательности { }, построенной из членов ряда   a_n, a_n ≥ 0, существует     = p, то ряд  a_n сходится при p < 1 и расходится при p > 1.

При p = 1 предельный признак Коши не дает ответа на вопрос, сходится данный ряд или расходится.

19) Интегральный признак (Коши, Маклорен).

Пусть данный ряд имеет вид   a_n =   f (n), причем f (n) есть значение в точке x = n некоторой функции f (x), определенной при x ≥ n₀. Если f (x) монотонно убывает и в области определения справедливо неравенство f (x) ≥ 0, то ряд   a_n сходится тогда и только тогда, когда сходится несобственный интеграл   f (x) dx.

20) Радикальный признак Коши — признак сходимости числового ряда:

Если для числового ряда с неотрицательными членами существует такое число d, 0 < d < 1, что, начиная с некоторого номера, выполняется неравенство 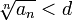 , то данный ряд сходится. 21) Признак Даламбера. а) Если существует натуральное число N такое, что для последовательности чисел qn =  , построенной из членов ряда   an, an > 0, для всех n ≥ N выполняется неравенство   ≤ q < 1 (q — фиксированное число, не зависящее отn), то ряд сходится; если для всех n ≥ N выполняется неравенство   ≥ 1, то ряд   an расходится. б) Если последовательность  , построенная из членов ряда   an, an > 0, имеет некоторый предел n,     =p, то при p < 1 ряд   an сходится, а при p > 1 расходится (предельный признак Даламбера). При p = 1 предельный признак Даламбера не дает ответа на вопрос, сходится данный ряд или расходится. 22) Ряд называется знакочередующимся, если его члены попеременно принимают значения противоположных знаков, т. 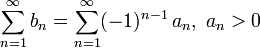е.: Признак Лейбница — признак сходимости знакочередующегося ряда, установлен Готфридом Лейбницем. Формулировка теоремы: Пусть для знакочередующегося ряда выполняются следующие условия: 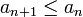 (монотонное невозрастание {an} по абсолютной величине)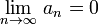 . Тогда этот ряд сходится.

23) Тейлора ряд, степенной ряд вида

 , (1)

где f (x) — функция, имеющая при х = а производные всех порядков. Во многих практически важных случаях этот ряд сходится к f (x) на некотором интервале с центром в точке а:

  (2)

(эта формула опубликована в 1715 Б. Тейлором). Разность R_n (x) = f (x) — S_n (x), где S_n (x) — сумма первых n + 1 членов ряда (1), называется остаточным членом Т. р. Формула (2) справедлива, если  . 

24) Маклорена ряд, исторически неправильное название (по имени К. Маклорена) степенного ряда вида:

 ,

где f(0), f’(0), f”(0), ..., f⁽ⁿ⁾(0),... – значения заданной функции f(x) и её последовательных производных при х = 0.Этот ряд был получен ранее Маклорена английским математиком Б. Тейлором (опубликовал 1715), что было известно и самому Маклорену. М. р. есть частный случай Тейлора ряда.