
- •Матрицы
- •А лгебра матриц
- •Вычисление обратной матрицы
- •Ранг матрицы
- •Системы линейных уравнений
- •Аналитическая геометрия
- •5 Видов уравнения на плоскости прямой.
- •Второй замечательный предел
- •Предел функции непрерывного аргумента
- •Первый замечательный предел
- •Непрерывность
- •Теорема о достаточном условии выпуклости функции
- •Теорема о необходимых условиях перегиба Теорема о достаточном условии точек перегиба
Линейная алгебра.
Определители (детерминант)
Назовем определителем число, записанное в виде квадратной таблицы чисел.
Ч![]()
![]()
![]()
![]() исло
элементов в строке (колонке) называют
порядком определителя.
исло
элементов в строке (колонке) называют
порядком определителя.
Для определителя справедливы 2 правила:
Это правило эквивалентных преобразований.
Правило раскрытия по строке (колонке).
Правило эквивалентных преобразований:
Если в определителе какую-то строку умножить на число не равное нулю (столбец) прибавить к другой строке (столбцу), то мы получим определитель эквивалентный данному.
П ример:


![]()
Правило раскрытия по строке:
Каждый определитель порядка n может быть представлен в виде суммы произведений элементов какой-либо строки (столбца) на их алгебраические дополнения.
![]()
![]()
А
![]()
![]() лгебраическим
дополнением Aij
к элементу aij
назовем
произведение (-1)i+jMij,
где M-
минор.
лгебраическим
дополнением Aij
к элементу aij
назовем
произведение (-1)i+jMij,
где M-
минор.
Минором, построенным по элементу aij , называется определитель порядка (n-1), полученный из исходного путем вычеркивания i строки и j столбца.
![]()
![]()
П![]()
 ример:
ример:
M
 11=|1|
11=|1|
Если в каком-то определителе есть строка (колонка), состоящая из нулей, то определитель равен нулю.
Определитель 2-го порядка равен разности произведений к элементу главной диагонали (СЗ, ЮВ) и элементов побочной диагонали (СВ, ЮЗ)
П римеры:
римеры:



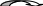


Матрицы
Матрицой называют прямоугольную таблицу чисел.
![]()

А лгебра матриц
![]()
![]()
![]()
Сложение:

Умножение:
![]()
![]()
![]()
Правило согласованности размерности матриц при умножении:
Количество столбцов 1-го сомножителя равняется количеству строк 2-го.
Чтобы получить элемент произведения двух матриц ij мы должны умножить i строчку 1-го сомножителя на j столбец 2-го и результаты сложить.
П ример:
ример:
![]()
Е - единичная матрица
Э то
квадратная матрица, у которой по главной
диагонали стоят единицы, а остальные
нули.
то
квадратная матрица, у которой по главной
диагонали стоят единицы, а остальные
нули.
![]()
![]() 1
1=1+1+1=3
1
1=1+1+1=3
12=3
21=0
22=0
Для всякой квадратной матрицы можно посчитать определитель.
Е сли
главный определитель квадратной матрицы
ноль, то матрица называется выражденной.
сли
главный определитель квадратной матрицы
ноль, то матрица называется выражденной.
Чтобы умножить матрицу на число, надо каждый элемент этой матрицы умножить на это число.
Вычисление обратной матрицы
![]()

Доказательство:


![]()
![]()
![]()
A 11=(-1)1+1*3=3
A12=-2
A21=-1
A22=1
Ранг матрицы
![]()
Р анг (rang) А- размерность наибольшего отличного от нуля определителя, содержащегося в матрице А.
Min (m,n)- максимально возможный порядок определителя.
П ример:

![]()
![]()
![]()
![]()
Системы линейных уравнений
Это система, у которой m уравнений и n неизвестных
О![]() бщий
вид
системы линейных уравнений
бщий
вид
системы линейных уравнений
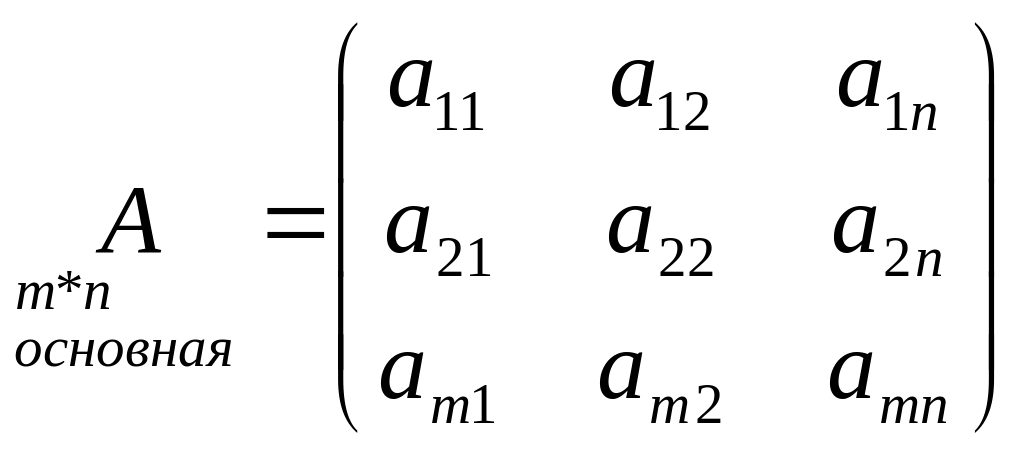



Матричная запись системы (10)
![]()
Д опущения:
А- квадратная, невырожденная
А-1Ax=A-1B x=A-1B (11) (решение системы 10)
Если количество неизвестных больше числа уравнений, то последнее (лишнее неизвестное) переходит в разряд параметров и переносится в правую часть.
Если основная матрица вырожденная, то отбрасывается последнее уравнение до тех пор, пока она не станет невырожденной.
Теорема Кронекера- Капелли:
С истема
(10)
имеет решения тогда и только тогда,
когда ранг основной матрицы системы
совпадает с рангом расширенной матрицы
(rang
A=
rang
A),
если при этом эти ранги совпадают с
числом неизвестных n,
то решение единственно. Если меньше n,
то решений бесконечно много.
истема
(10)
имеет решения тогда и только тогда,
когда ранг основной матрицы системы
совпадает с рангом расширенной матрицы
(rang
A=
rang
A),
если при этом эти ранги совпадают с
числом неизвестных n,
то решение единственно. Если меньше n,
то решений бесконечно много.

![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Векторная алгебра
![]()
Y



 a2
a2

 a
a

 0
a1
X
0
a1
X
Умножение вектора на число:
![]()
С
![]()
![]() ложение
и вычитание:
ложение
и вычитание:
![]()
![]()
![]()
Умножение векторов:
а) Скалярное произведение:
![]()
к оммутативно
![]()
б) Векторное произведение (3-х мерное):
![]()
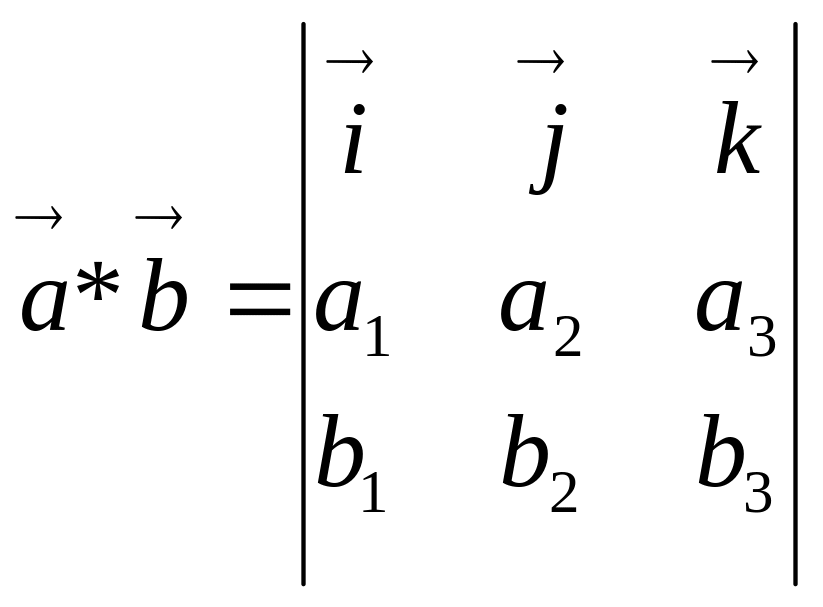
![]()
![]() i
i![]() ,j,k-
орты осей координат
,j,k-
орты осей координат

![]()
![]()

![]()
![]()



![]()

![]()
![]()
![]()
С войство антикоммутативности
![]()
Геометрический определитель второго порядка равен длине векторного произведения векторов, составленных из строк данного определителя.

Геометрическое смешенное произведение:
О но
равно объему параллелепипеда, построенного
на исходных векторах.
но
равно объему параллелепипеда, построенного
на исходных векторах.
