6. Линия с распределенными параметрами без искажений

Сигналы, передаваемые по линиям связи, являются несинусоидальными функциями времени и состоят из суммы гармоник различных частот. Если в ли­нии созданы неодинако­вые условия для различных гармоник, то в конце линии гармонический состав сигнала будет отличаться от гармонического состава этого же сигнала в начале линии, т.е. сигнал будет ис­кажен. Для линий связи очень важным условием является создание такого режима работы, при котором отсутствовало бы искажение сигнала.

Различают два вида искажений сигнала амплитудные и фазовые. Ампли­тудные иска­жения имеют место в том случае, когда коэффициент затухания α зависит от частоты, при этом амплитуды отдельных гармоник затухают с не­одинаковой скоростью, что приводит к искажению формы сигнала. Фазовые ис­кажения возникают в том случае, когда фазовая ско­рость υ зависит от частоты, при этом происходит сдвиг отдельных гармоник по фазе, что приводит к иска­жению формы сигнала. Итак, искажение сигнала будет отсутствовать при по­стоянстве двух параметров: α = const, υ = const.

Вторичные параметры линии и зависят от частоты, что в общем слу­чае создает в линии неодинаковые условия для прохождения волн напряжения и тока различных частот и такая линия является искажающей.

Отсутствие искажений в линии наблюдается только при определенном соотношении между ее первичными параметрами.

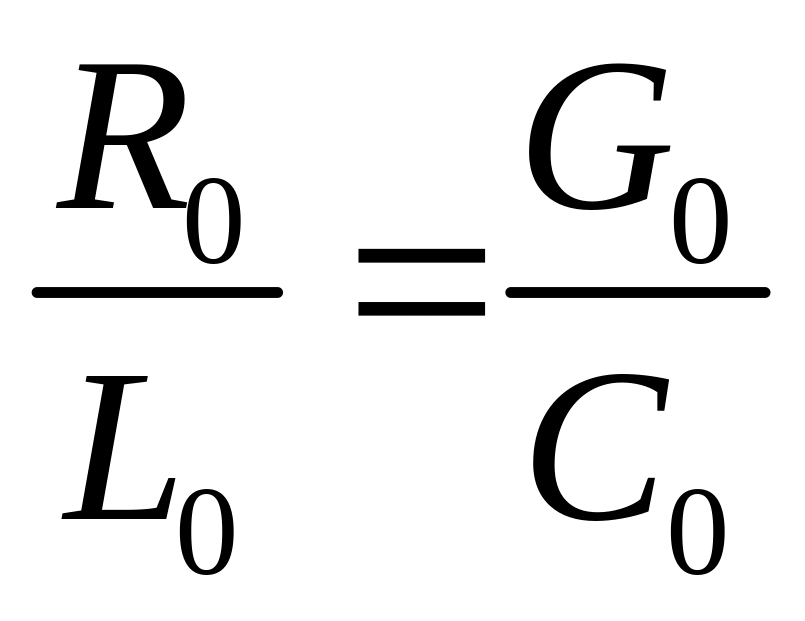или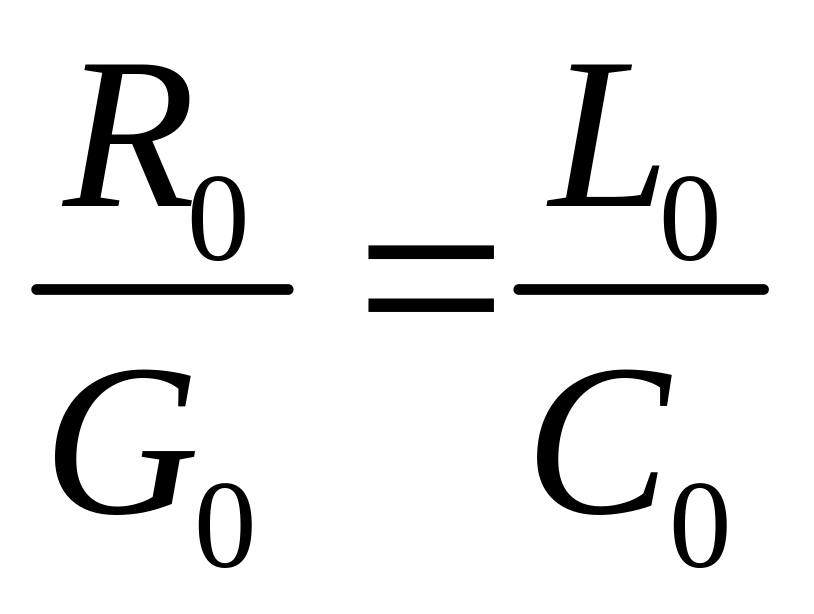

При соблюдении этого условия получим:

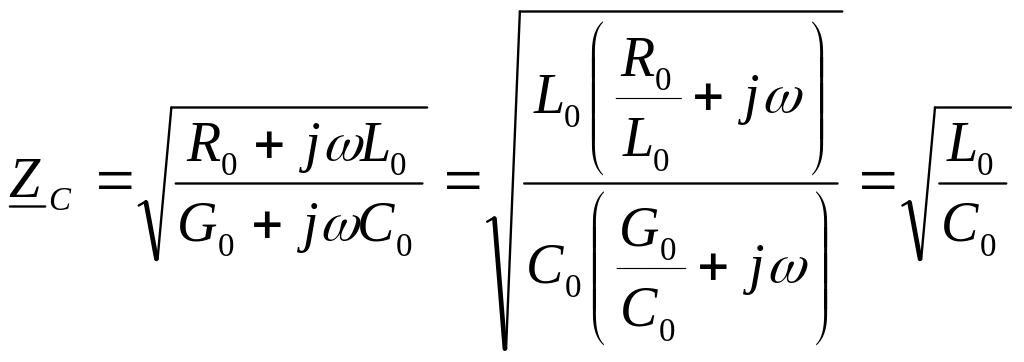
 волновое сопротивление линии является чисто активным и не зависит от час­тоты;

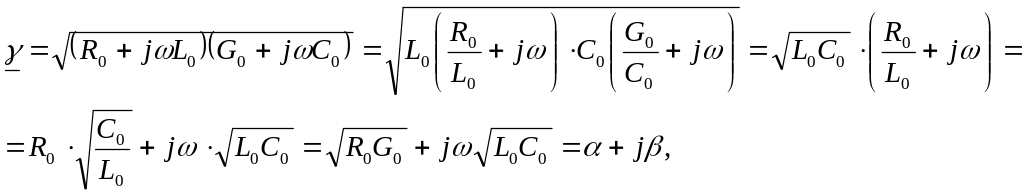
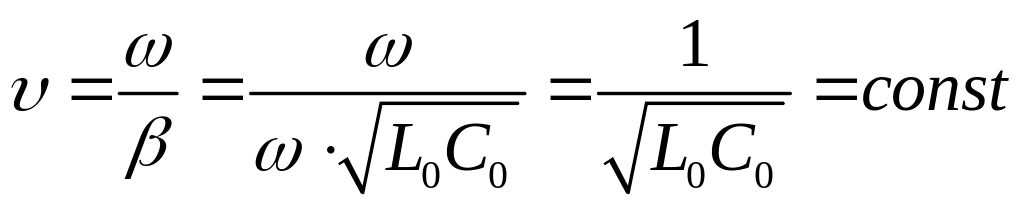
где  коэффициент затухания не зависит от частоты,  ко­эффициент фазы,  фазовая скорость не зависит от час­тоты.

В реальных кабельных линиях связи соотношение между первичными па­раметрами 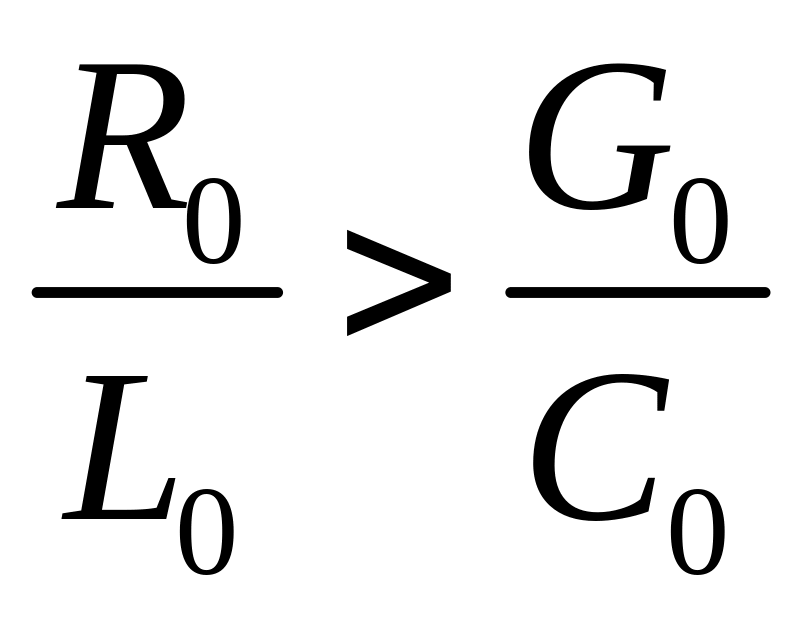, так как вследствие совершенства изоляции активная про­водимость G₀ очень мала. Режим без искажений может быть получен искусст­венно путем включения в рассечку линии через определенные интервалы до­полнительных катушек индуктивности L_д из условия 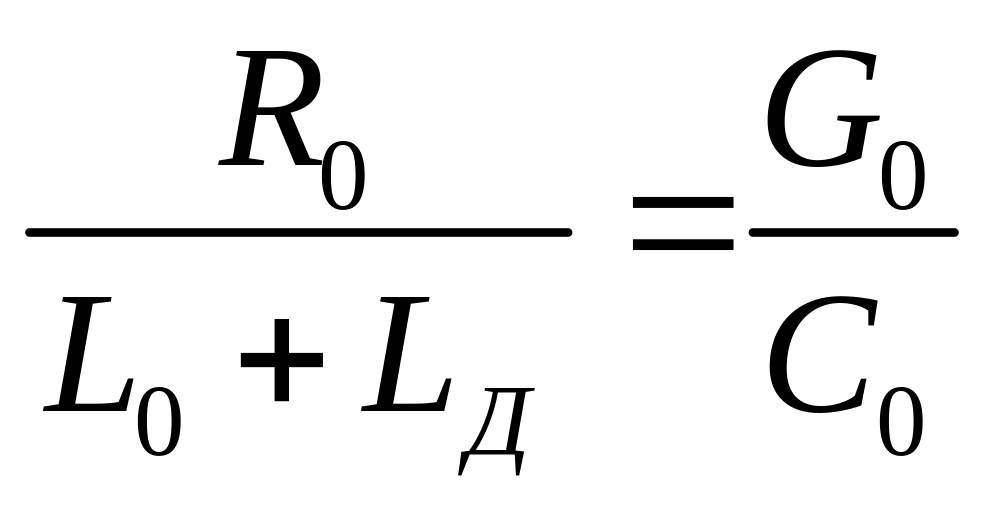. Однако с уве­личением эквивалентной индуктивности снижается фазовая ско­рость υ, в результате чего увеличивается общее время прохождения сигнала Т, которое по техническим нормам не должно превышать определенную вели­чину.

Реальные линии связи в своем большинстве являются искажающими, а искажения сигналов на приемных концах линии устраняются с помощью специ­альных корректирующих устройств.

7. Линия с распределенными параметрами без потерь

Для кабельных линий с распределенными параметрами, работающих на высоких час­тотах (линии связи), реактивные параметры значительно превосхо­дят активные и . При расчете режимов таких линий можно без особого ущерба для точности рас­чета пренебречь активными параметрами и принять их равными нулю . В таком случае линия становится иде­альной или без потерь.

Волновое сопротивление линии без потерь:



является чисто активным и не зависит от частоты.

Постоянная распространения линии без потерь:

,

где

В линии без потерь отсутствует затухание сигнала , а фазовая ско­рость v не зависит от частоты, следовательно, линия без потерь является неис­кажающей.

Учитывая математические соотношения, что , и

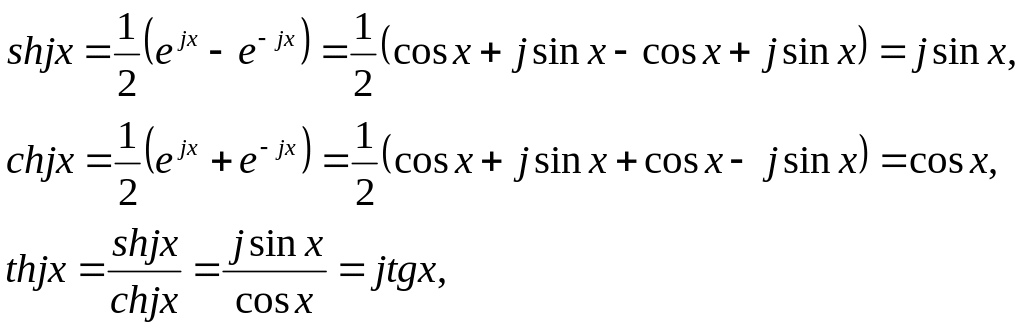
преобразуем комплексные уравнения установившегося синусоидального режима ли­нии:

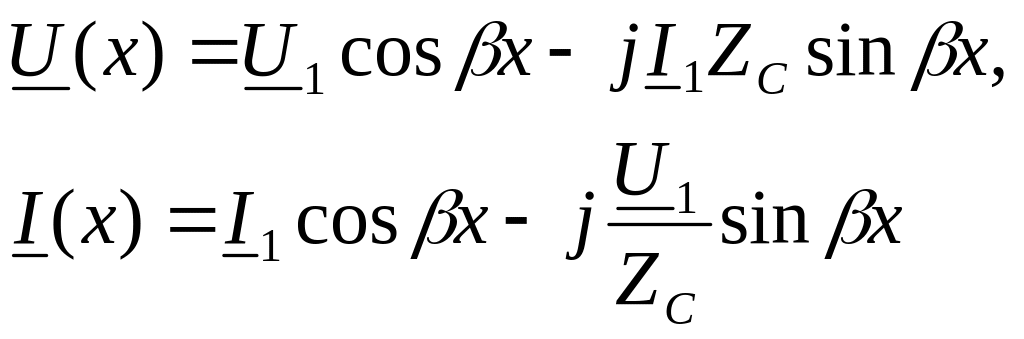
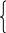 при отсчете координаты х от начала ли­нии,

 при отсчете координаты y от конца ли­нии,

 входное сопротивление линии.

Режим линии без потерь определяется свойствами (параметрами) самой линии и ве­личиной и характером нагрузки на ее конце. Исследуем работу линии в различ­ных режимах нагрузки.

1.Режим согласованной нагрузки: .

Учитывая, что , комплексные уравнения линии получат следую­щий вид:

 при отсчете координаты y от конца линии,

 входное сопротивление линии.

В режим согласованной нагрузки напряжение u(t,y) и ток i(t,y) состоят только из па­дающих волн, которые распространяются от начала линии к ее концу без затухания. Дейст­вующие значения напряжения U(y) и тока I(y) не за­висят от координаты у и во всех точках линии имеют одинаковые значения.

Входное сопротивление линии равно волновому и не зави­сит от длины линии. Графические диаграммы названных функций пока­заны на рис. 157

2.Режим холостого хода: Комплексные уравнения ре­жима линии при отсчете координаты y от конца ли­нии получат вид:

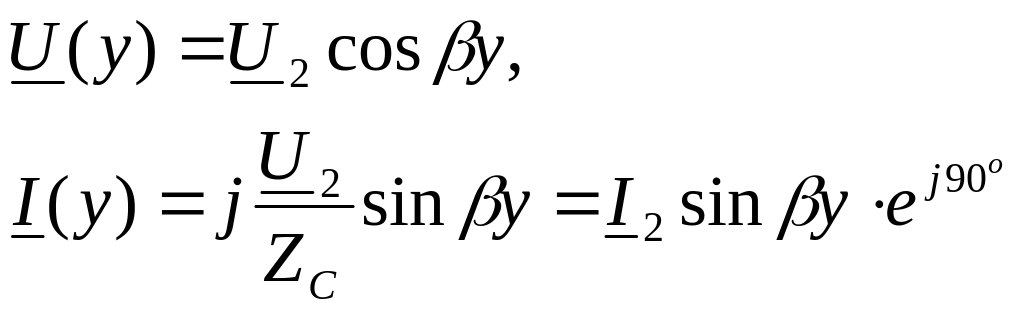
Входное сопротивление ли­нии:

Входное сопротивление линии Z₁(у) является чисто реактивным, его ве­личина и ха­рактер зависят от длины линии.