18. Биномиальное, геометрическое, гипергеометрическое распределение, их среднее и дисперсия.

Пусть имеются n испытаний Бернулли с вероятностью успеха p и неуспеха q, р + q = 1.

Дискретная СВ Х – число успехов имеет распределение

p_k= Р(Х = k) = , k =0,1, 2,…,n.

Это распределение называется биномиальным с параметрами p и q. Заметим, что сумма вероятностей

=(p+q)ⁿ=1

Математическое ожидание и дисперcия CВ Х:

МХ = nр, DX = npq.

Максимум вероятностей р_k дocтигaется при k = [nр - q]+1

Дискретная СВ Х имеет геометрические распределение, если она принимает значения k=1,2,3,…(счетное множество значений) с вероятностями

p_k= Р(Х = k)=pq^k-1, k=1,2,3,…,

где 0<p<1, q=1-p

Определение является корректным, так как сумма вероятностей

СВ Х, имеющая геом распред, представляет собой число испытаний Бернулли до первого успеха.

Мат ожидание и дисперсия Х: MX=1/p, DX=q/p².

Дискретная СВ Х имеет гипергеометрические распределение, если она принимает значения m с вероятностями

где m=1,2,…,k; k=min(n,M); M≤N; n≤N. Вероятность p_m явл вероятность выбора m объектов, обладающих заданным свойством, из множества n объектов, случайно извлеченных(без возврата) из совокупности N объектов, среди которых M объектов обладают заданным свойством.

Мат ожидание и дисперсия случайной величины, имеющей гипергеометрическое распределение с параметрами n,M,N:

MX=nM/N; DX=n

19 Распределение Пуассона

CВ Х распределена по закону Пуассона, если она принимает целые значения 0,1,2,… с вероятностями

p_k= Р(Х = k) =

где λ> 0 – параметр распределения. При этом

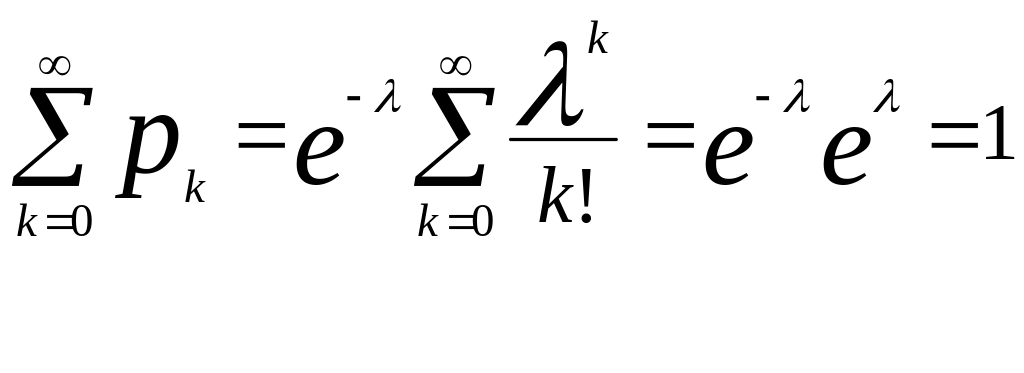
Мат ожидание идисперсия пуассоновской СВ равны параметру распределения:

MX= λ;DX=λ.

20.Непрерывные случайные величины, функция распределения и функция плотности вероятностей

X, Fx(X)=P(X<x)

X-непрерывная; Fx-непрерывная

X имеет плотность распределение вероятности если сущ-ет на отрезке числовая фун-ция p(x), такая что

Fx(X)=

P(a≤x<b)=F(b)-F(a)

Св-ва непрер СВ:

1. P(X=x_o)=0

Через предел

Lim x_{o →}a

P(a≤x<х_о)=F(х_о)-F(a) x_{o →}a

P(a≤x<b)=

21. Равномерное распределение и его характеристики.

Непрерывная СВ Х распределена равномерно на отрезке [a;b], если ее плотность вероятности р(х) постоянна на этом отрезке и равна нулю вне его, т.е. р(х)= ,,,1-𝑏−𝑎. , 𝑎≤𝑥≤𝑏-0, 𝑥<𝑎, 𝑥>𝑏.. (время ожидания транспорта, кот. приходит случайно на остановку)

Ф-ия распределения СВ, распределенной по равномерному закону, имеет вид: f(x)=

Мат. ожидание и дисперсия равномерной СВ:

МХ= ; DX=

22. Переход от непрерывной СВ к дискретной, έ-сеть.

X -сеть >0

закидываем сеть

считаем вероятности

получаем таблицу

23. Показательное распределение.

Непрерывная СВ Х имеет показательное распределение с параметром λ, если ее плотность вероятности имеет вид p(x)= , где λ 0 (время непрерывн. работы прибора). Ф-ия распределения СВ, распределенной по показательному закону, равна F(x)= Графики ф-ии распределения и плотности вероятности:

Мат. ожидание и дисперсия показательно распределенной СВ Х: MX= ; DX=

24. Нормальная СВ.

если есть СВ, которая имеет много факторов и ни один из которых не превалирует, то эта величина будет нормальной (пример: рост человека). Непрерывная СВ Х имеет нормальное распределение (закон Гаусса) с параметрами a и (сигма), если ее плотность вероятности имеет вид: p(x)= , где 0. Ф-ия распределения нормальной СВ Х:

MX=a; DX=

график плотности вероятности нормального распределения:

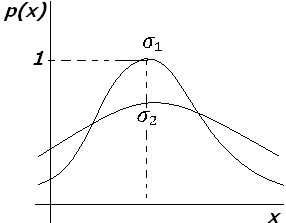
Выделяется стандартнаянормальная СВ при a=0 и =1. Для стандартного распределения плотность равна

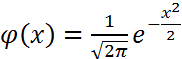, а ф-ия распределения