
- •Дополнительные вопросы к устному собеседованию
- •6. Что называется бинарным отношением в множестве а? Сформулируйте определение и приведите пример бинарного отношения в множестве.
- •Любой элемент х, принадлежащий классу эквивалентности [a], называется представителем этого класса.
- •10. Что называется разбиением множества а? Сформулируйте определение и приведите пример разбиения множества.
- •26. Закончите определение «Упорядоченное множество называется вполне упорядоченным, если ...». Приведите примеры вполне упорядоченного множества и множества, не являющегося таковым.
- •27. Закончите определение «Множество а называется равномощным множеству в, если ...». Приведите примеры равномощных и неравномощных множеств.
- •28. Закончите определение «Множество а называется счетным, если ...». Приведите примеры счетных и несчетных множеств.
- •30. Что такое булеан множества а, и что Вы знаете о его мощности?
- •31. Сформулируйте аксиому метода полной математической индукции.
- •1. Полная математическая индукция
- •32. Какой метод рассуждений называется неполной индукцией?
- •33. Какой метод рассуждений называется полной индукцией?
- •34. Сформулируйте правило суммы для конечных непересекающихся множеств а и Булеанам множества а называется совакупность всех его подмножеств, включая пустое множество и само множество а.
- •44. Выпишите треугольник Паскаля и объясните смысл входящих в него чисел.
- •45. Чему равно число всех подмножеств n-элементного множества?
Дополнительные вопросы к устному собеседованию
Что называется объединением множеств А и В? Сформулируйте определение и проиллюстрируйте его с помощью кругов Эйлера.
Объединением
множеств Х и У называется множество
Х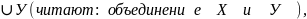 состоящее
из элементов, принадлежащих хотя
бы одному из множеств Х или У.
состоящее
из элементов, принадлежащих хотя
бы одному из множеств Х или У.
2.Что называется пересечением множеств А и В? Сформулируйте определение и проиллюстрируйте его с помощью кругов Эйлера.
Пересечением
множеств
Х и У называется множество Х состоящее
из элементов, принадлежащих как
множеству
Х, так и
множеству У.
состоящее
из элементов, принадлежащих как
множеству
Х, так и
множеству У.
3.Что называется разностью множеств А и В? Сформулируйте определение и проиллюстрируйте его с помощью кругов Эйлера.
Разностью множеств Х и У называется множество Х \ У, состоящее из элементов множества Х, не принадлежащих множеству У.
4. Что называется дополнением множества А до множества В? Сформулируйте определение и проиллюстрируйте его с помощью кругов Эйлера.
Если множесто Х – подмножество множества У (Х ⊂ У), то разность У \ Х называют дополнением множества Х до множества У и обозначают символом СУХ.
Итак, СУХ = У \ Х.
Операцию нахождения дополнения подмножества до множества также называют дополнением.
5. Что называется прямым (декартовым) произведением множества А на множество В? Сформулируйте определение и проиллюстрируйте его на примере
Декартовым
(прямым) произведением
множеств А1,
А2,
… , Аn
называется множество А1 А2
…
Аn
, состоящее из упорядоченных наборов
(а1,
а2,
… , аn)
их элементов, взятых по одному из каждого
множества: а1
А2
…
Аn
, состоящее из упорядоченных наборов
(а1,
а2,
… , аn)
их элементов, взятых по одному из каждого
множества: а1
 А1,
а2
А2,
… , аn
Аn.
А1,
а2
А2,
… , аn
Аn.
Кратко: А1 А2 … Аn = {(а1, а2, … , аn) | а1 А1, а2 А2, … , аn Аn}.
В частности, А В = {(x, y) | x А, y В}.
По
определению принимают, что А
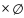 =
=
 А
=
=
.
А
=
=
.
Декартово
произведение А
 называют декартовым
квадратом
или просто квадратом
множества
А и обозначают символом А2.
Т.о.,
называют декартовым
квадратом
или просто квадратом
множества
А и обозначают символом А2.
Т.о.,
А2
= А
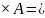 {(x,
y)
| x
А, y
А}.
{(x,
y)
| x
А, y
А}.
Операцию нахождения декартового произведения множеств называют декартовым умножением множеств.
6. Что называется бинарным отношением в множестве а? Сформулируйте определение и приведите пример бинарного отношения в множестве.
Определение 1. Бинарное отношение во множестве А – это правило, позволяющее составлять упорядоченные пары (х, у) из элементов х, у множества А.
Другое, близкое по смыслу, но не идентичное данному, определение таково:
Определение 2. Бинарным отношением в множестве А называют любое подмножество Р декартова произведения А А (декартова квадрата А2).
Согласно этому определению
Р ⊂ А А.
Пример 1. Пусть А = {1, 2, 3}. Зададим в множестве А бинарное отношение Р правилом:
«хРу (элемент х находится в отношении Р с элементом у) тогда и только тогда, когда х ≤ у».
(с точки зрения логики правило задано в форме двуместного предиката).
В данном случае, бинарное отношение Р задано словесным правилом. Его естественно назвать отношением «не больше». Символ ≤ также можно было бы принять в качестве обозначения данного бинарного отношения.
Очевидно, этому правилу удовлетворяют только следующие упорядоченные пары элементов множества А:
(1, 1), (1, 2), (1, 3), (2, 2), (2, 3), (3, 3).
7. Что называется отношением эквивалентности в множестве А? Сформулируйте определение и приведите пример отношения эквивалентности в множестве.
Отношение Р в множестве А называется отношением эквивалентности, если оно удовлетворяет трем условиям:
1) аРа, а А (рефлексивность);
2)
аРв
 вРа, а, в
А (симметричность);
вРа, а, в
А (симметричность);
3) аРв, вРс ⇒ аРс, а, в, с А (транзитивность).
Пример 1. Отношение ⇈ сонаправленности лучей во множестве А ориентированных лучей на плоскости (в пространстве).
В самом деле, во-первых, это – бинарное отношение на А, т.к. позволяет пары лучей по указанному принципу.
Во-вторых, выполняются условия 1) – 3):
1) а ⇈ а, а А;
2) а ⇈ в в ⇈ а, а, в А;
3) а ⇈ в, в ⇈ с ⇒ а ⇈ с, а, в, с А.
Пример 2.Отношение = равенства фигур на плоскости (в пространстве).
В самом деле, во-первых, это – бинарное отношение в А, т.к. позволяет пары лучей по указанному принципу.
Во-вторых, выполняются условия 1) – 3):
1) а = а, а А;
2) а = в в = а, а, в А;
3) а = в, в = с ⇒ а = с, а, в, с А.
8. Что называется классом эквивалентности элемента а множества А, относительно заданного в нем отношения эквивалентности? Сформулируйте определение и приведите пример класса эквивалентности элемента множества.
Классом
эквивалентности элемента
а множества А по отношению
 называется множество [a]
, состоящее из элементов этого множества,
эквивалентных элементу а:
называется множество [a]
, состоящее из элементов этого множества,
эквивалентных элементу а:
[a] = {x A | x а}.
