
- •Двойной интеграл
- •2. Двойной интеграл
- •4. Тройной интеграл
- •5. Тройной интеграл
- •6. Тройной интеграл
- •7. Замена переменных в тройном интеграле
- •9. Приложения тройного интеграла
- •10. Криволинейный интеграл первого рода
- •11. Вычисление криволинейного интеграла первого рода.
- •12. Криволинейный интеграл 2-го рода
- •18. Ряды.
- •19Ряды.Св-ва рядов
- •20. Необх. Признак сходимости
- •25. Знакочередующийся ряд.
- •26. Знакопеременный числовой ряд.
- •30. Разложение функции в степенной ряд. Формулы Тейлора и Маклорена.
18. Ряды.
Пусть
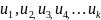 ,
где
,
где
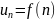 -
бесконечная числовая последовательность.
Выражение
-
бесконечная числовая последовательность.
Выражение
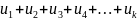 - бесконечный числовой ряд, а
,
- члены ряда.
- бесконечный числовой ряд, а
,
- члены ряда.
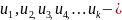 числовая
последовательность nЄN
числовая
последовательность nЄN
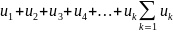
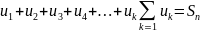 -
n-ая
частичная сумма ряда nЄN
-
n-ая
частичная сумма ряда nЄN
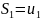
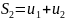
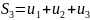
…

 последовательность
n-ых
частичных сумм ряда
последовательность
n-ых
частичных сумм ряда

Числовой
ряд называется сходящимся, если
существует предел
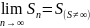
 для расходящихся
рядов эта запись не имеет смысла
для расходящихся
рядов эта запись не имеет смысла
 общий член ряда,
задается формулой
общий член ряда,
задается формулой

 не существует
не существует ряд
расходится!
ряд
расходится!
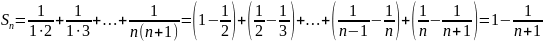
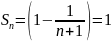 - сумма ряда→ряд
сходится
- сумма ряда→ряд
сходится
Эталонные
ряды:
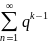 /q/≥1-расходящийся;
/q/<1
– ряд сходящийся.
/q/≥1-расходящийся;
/q/<1
– ряд сходящийся.
 гармонический
ряд, расходящийся!
гармонический
ряд, расходящийся!
 /q/≤1-расходящийся;
/q/>1
– ряд сходящийся.
/q/≤1-расходящийся;
/q/>1
– ряд сходящийся.
Осн. Виды рядов: положительные, знакочередующиеся, знакопеременные, степенные, функциональные.
19Ряды.Св-ва рядов
Пусть , где - бесконечная числовая последовательность. Выражение - бесконечный числовой ряд, а , - члены ряда.
Числовой ряд называется сходящимся, если существует предел
для расходящихся рядов эта запись не имеет смысла
Свойства сходящихся рядов:
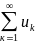 сход-ся→
сход-ся→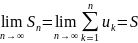 сумма ряда
сумма ряда
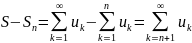 остаток ряда Rn
остаток ряда Rn
Св-во
1. Если ряд сходится, то последовательность
Rn
является бесконечно малой
последовательностью. Док-во :Rn=
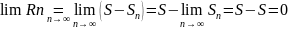 Св-во 2: Н.у. если ряд сходится, то предел
Св-во 2: Н.у. если ряд сходится, то предел
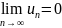 Док-во : сущ-ет
Док-во : сущ-ет
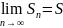
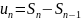
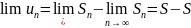 =0
=0
Если
ряд сходится, то предел
,
но обратное не верно, но достаточное
условие для расходимости:
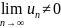 - ряд расходится.
- ряд расходится.
Св-во
3: отбрасывание или добавление сколько
угодно n
первых членов ряда не влияет на
сходимость.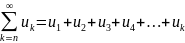 ;
;
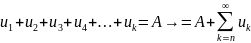

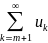

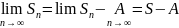
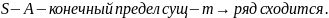
Св-во
4: если каждый член ряда умножить на
какое-либо число, то это не влияет на
сходимость.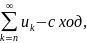
 - сход, =
- сход, =
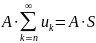
20. Необх. Признак сходимости
Пусть , где - бесконечная числовая последовательность. Выражение - бесконечный числовой ряд, а , - члены ряда.
Числовой ряд называется сходящимся, если существует предел
для расходящихся рядов эта запись не имеет смысла
Если ряд сходится, то последовательность Rn является бесконечно малой последовательностью. Док-во :Rn= Св-во 2: Н.у. если ряд сходится, то предел Док-во : сущ-ет =0
Если ряд сходится, то предел , но обратное не верно, но достаточное условие для расходимости: - ряд расходится.
21.
Числовой ряд
– знакополож.
 (1), если все
>0
(1), если все
>0
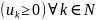
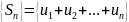
Если
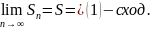
для (1) будет неубывающ. Или возраст. Последовательно
1) если
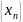 сходится, то она ограничена.
сходится, то она ограничена.
2) если монотонна, ограничена, то она сходится
Т1(признак сравнения)
Пусть даны 2 знакоположит. Числ. Ряда
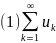
(2)
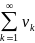 пусть
пусть
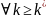 :
:
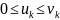 :
:
1)
из сходимости ряда 2
2) из расходимости ряда 1 следует расходимость ряда 2
1) докажем: Пусть дано что сходится(2):

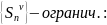
(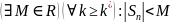
Тогда
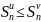 из нер-ва следует ограниченность
последовательности ряда (1) и это значит
что (1) сходится
из нер-ва следует ограниченность
последовательности ряда (1) и это значит
что (1) сходится
2)
ряд (1) расходится
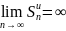
 (2)
расх.
(2)
расх.
Признак
сравнения применяется для рядов, у
которых постоянная степень:
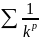 ….эти
ряды нужно сравнивать с эталонным
рядом.
….эти
ряды нужно сравнивать с эталонным
рядом.
Т2( признак сравнения в предельной форме)
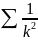 –сход.
–сход.
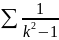
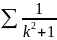 - ряд сход. Из Т1
- ряд сход. Из Т1
 =>
сход.
=>
сход.
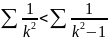 =>
ряд может сход. И расход.
=>
ряд может сход. И расход.
Пусть
:
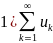
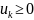 знакоположительные
знакоположительные
2)
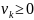
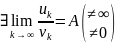 ,тогда 1 и 2 сходятся
или расходятся одновременно
,тогда 1 и 2 сходятся
или расходятся одновременно
 =1 =>ряд
=1 =>ряд

22. Числовой ряд – знакополож. (1), если все >0
Если
для (1) будет неубывающ. Или возраст. Последовательно
1) если сходится, то она ограничена.
2) если монотонна, ограничена, то она сходится
Признак Даламбера
Пусть
;

Тогда q>1 ряд расходится ; q<1 ряд сходится
Док-во:
 начиная
с
начиная
с
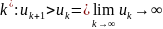 не выполнено необходимое условие
сходимости ряда, а если оно не выполнено
=> ряд расход-ся
не выполнено необходимое условие
сходимости ряда, а если оно не выполнено
=> ряд расход-ся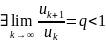 (
(
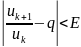
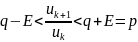 ,
но р <1
,
но р <1
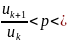 1
1
 р
р
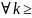 1
u2<p*u1;
u3<p*u2<p^2*u1; u4<p*u3<p^3*u1…..
1
u2<p*u1;
u3<p*u2<p^2*u1; u4<p*u3<p^3*u1…..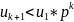 ,
,
тогда , р<1
ср.
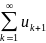 с р
с р
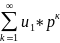 -
сход.=>
тоже сход-ся.
-
сход.=>
тоже сход-ся.
Замечание к признаку Даламбера
Если
в пр. Даламбера
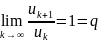 ,
то признак не дает ответа.
,
то признак не дает ответа.
Признак
применяется если (к! или
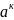 )
)
23. Числовой ряд – знакополож. (1), если все >0
Если
для (1) будет неубывающ. Или возраст. Последовательно
1) если сходится, то она ограничена.
2) если монотонна, ограничена, то она сходится
Радикальный признак Коши
(1)
Если
 =
q
=
q
При q>1 расход
q<1 сход
Док-во
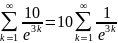

 <1
сход
<1
сход
Замечание 1: q=1, признак Коши не дает ответа на вопросы сходимости ряда
Замечание
2: Док-во: если
=q,
то
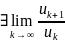 =q
=q
Признак Коши сильнее Даламбера, если Даламбер не работает, применяют Коши.
Замечание 3: ( )
Замечание
4: известный
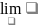
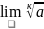 =1
(а>0)
=1
(а>0)
 =1
=1
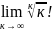 =
=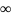
 =0
=0
24. Числовой ряд – знакополож. (1), если все >0
Если
для (1) будет неубывающ. Или возраст. Последовательно
1) если сходится, то она ограничена.
2) если монотонна, ограничена, то она сходится
Интегральный признак Коши - Макларена
Рассмотрим ряд (1),
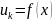 ;
f(x)
x
;
f(x)
x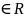
T: если фун-я f(x) –невозраст.
 с
несобственным интегралом
с
несобственным интегралом

Sвход

f(2)+f(3)+…f(n)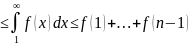
u2+u3+…+

Sn-n1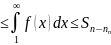
1)Пусть
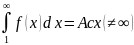
Sn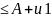 – огр.(по кр. Ряд сходится)
– огр.(по кр. Ряд сходится)
2)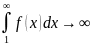 -
расх.
-
расх.
Sn

Если
интеграл расх. то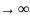 и сумма тоже стремится к
=>
интеграл расход.
и сумма тоже стремится к
=>
интеграл расход.
 ;
f(x) =
;
f(x) =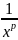
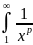 dx
=
dx
=

 –расх.
–расх.

 (
p>1
– сход. р<1 – расх. ) эталонный ряд
(
p>1
– сход. р<1 – расх. ) эталонный ряд
