
- •Глава1. Сущность прогнозирования
- •Глава2.Пример построения прогноза по эконометрической модели
- •Глава 1. Сущность прогнозирования
- •Понятие прогнозирования и его особенности
- •Точечное и интервальное прогнозирование
- •1.3 Условное и безусловное прогнозирование
- •1.4 Прогнозирование при наличии авторегрессии ошибок
- •Глава2. Пример построения прогноза по эконометрической модели
- •2.1. Точечное и интервальное прогнозирование, основанное на модели линейной регрессии
Точечное и интервальное прогнозирование
В
прогнозных расчетах по уравнению
регрессии определяется предсказываемое
(уp)
значение как точечный прогноз
 при хp=хk,
т. е. путем подстановки в уравнение
регрессии
при хp=хk,
т. е. путем подстановки в уравнение
регрессии
 соответствующего
значения х. Однако точечный прогноз
явно не реален. Поэтому он дополняется
расчетом стандартной ошибки
,
т. е.
соответствующего
значения х. Однако точечный прогноз
явно не реален. Поэтому он дополняется
расчетом стандартной ошибки
,
т. е.
 и
соответственно интервальной оценкой
прогнозного значения (у*)
и
соответственно интервальной оценкой
прогнозного значения (у*)
- <у*< + (1.1)
Чтобы понять, как строится формула для определения величин стандартной ошибки , обратимся к уравнению линейной регрессии:
 (1.2)
(1.2)
Подставим в это уравнение выражение параметра b1:
b1= -b0
-b0
тогда уравнение регрессии примет вид:
= -b0 +b0 x= +b0(x- ) (1.3)
Отсюда вытекает, что стандартная ошибка зависит от ошибки и ошибки коэффициента регрессии b0, т. е.
2
= (1.4)
(1.4)
Из
теории выборки известно, что
 .
Используя в качестве оценки σ2
остаточную
дисперсию на одну степень свободы S2,
получим формулу расчета ошибки среднего
значения переменной у:
.
Используя в качестве оценки σ2
остаточную
дисперсию на одну степень свободы S2,
получим формулу расчета ошибки среднего
значения переменной у:
 (1.5)
(1.5)
Ошибка коэффициента регрессии, как уже было показано, определяется формулой
 ∑
∑ (1.6)
(1.6)
Считая, что прогнозное значение фактора хp=хk, получим следующую формулу расчета стандартной ошибки предсказываемого по линии регрессии значения, т. е.
 ∑
∑ =
= (1.7)
(1.7)
Соответственно имеет выражение:
 (1.8)
(1.8)
Рассмотренная
формула стандартной ошибки предсказываемого
среднего значения у при заданном значении
хk
характеризует ошибку положения линии
регрессии. Величина стандартной ошибки
как
видно из формулы, достигает минимума
при хк
= ,
и возрастает по мере того, как «удаляется»
от
в любом направлении. Иными словами, чем
больше разность между хк
и х, тем больше ошибка
с которой предсказывается среднее
значение у для заданного значения хk.
Можно ожидать наилучшие результаты
прогноза, если признак- фактор х находится
в центре области наблюдений х и нельзя
ожидать хороших результатов прогноза
при удалении хк
от
.
Если же значение хк
оказывается
за пределами наблюдаемых значений х,
используемых при построении линейной
регрессии, то результаты прогноза
ухудшаются в зависимости от того,
насколько хк
отклоняется
от области наблюдаемых значений фактора
х.
,
и возрастает по мере того, как «удаляется»
от
в любом направлении. Иными словами, чем
больше разность между хк
и х, тем больше ошибка
с которой предсказывается среднее
значение у для заданного значения хk.
Можно ожидать наилучшие результаты
прогноза, если признак- фактор х находится
в центре области наблюдений х и нельзя
ожидать хороших результатов прогноза
при удалении хк
от
.
Если же значение хк
оказывается
за пределами наблюдаемых значений х,
используемых при построении линейной
регрессии, то результаты прогноза
ухудшаются в зависимости от того,
насколько хк
отклоняется
от области наблюдаемых значений фактора
х.
Фактические
значения у варьируют около среднего
значения
Индивидуальные
значения у могут отклоняться от
на величину случайной ошибки ε , дисперсия
которой оценивается как остаточная
дисперсия на одну степень свободы S2.
Поэтому ошибка предсказываемого
индивидуального значения у должна
включать не только стандартную ошибку
 ,
но и случайную ошибку S.
,
но и случайную ошибку S.
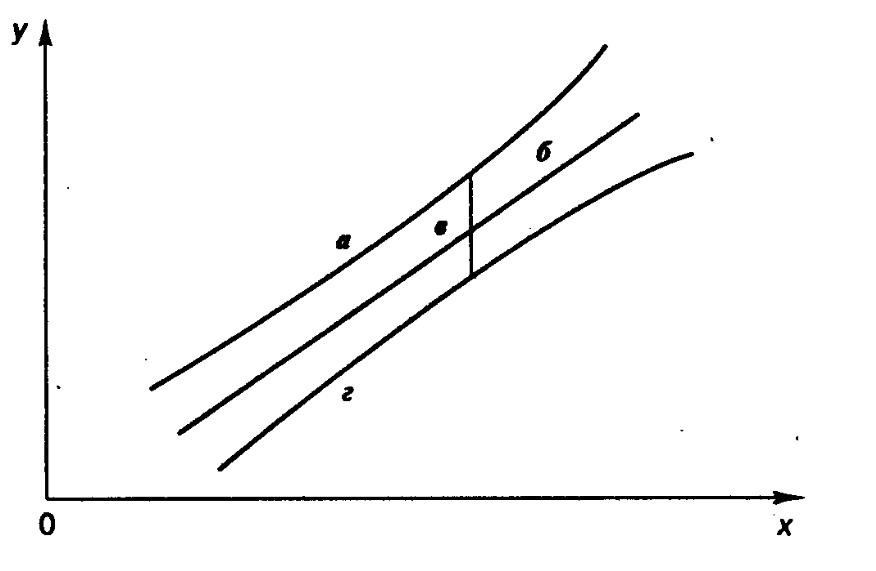
Рис. 1 Доверительный интервал линии регрессии: а — верхняя доверительная граница; б — линия регрессии; в — доверительный интервал для при хк; г — нижняя доверительная граница
Средняя
ошибка прогнозируемого индивидуального
значения у
 составит:
составит:
 (1.9)
(1.9)
При прогнозировании на основе уравнения регрессии следует помнить, что величина прогноза зависит не только от стандартной ошибки индивидуального значения у, но и от точности прогноза значения фактора х. Его величина может задаваться на основе анализа других моделей исходя из конкретной ситуации, а также из анализа динамики данного фактора. Рассмотренная формула средней ошибки индивидуального значения признака у( ) может быть использована также для оценки существенности различия предсказываемого значения исходя из регрессионной модели.[6]
