4. Эллиптическая, круговая и линейная поляризация гармонических волн. Степень поляризации.

Поляриза́ция волн — явление нарушения симметрии распределения возмущений в поперечной волне (например, напряжённостей электрического и магнитного полей в электромагнитных волнах) относительно направления её распространения. В продольной волне поляризация возникнуть не может, так как возмущения в этом типе волн всегда совпадают с направлением распространения.^[1]

Поперечная волна характеризуется двумя направлениями: волновым вектором и вектором амплитуды, всегда перпендикулярным к волновому вектору. Так что в трёхмерном пространстве имеется ещё одна степень свободы — вращение вокруг волнового вектора.

Рассмотрим электромагнитное поле в той области пространства, где отсутствуют источники 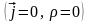, - свободное электромагнитное поле. В этом случае электрическое и магнитное поля подчиняются однородной системе уравнений Максвелла: .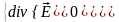

Вычисляя 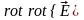и используя выражение для 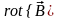, получим волновое уравнение: .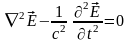

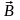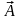Аналогичное уравнение получается и для магнитного поля . Если потенциалы и подчинить условию Лоренца (4.6), то уравнения (4.7) для потенциалов электромагнитного поля превращаются в волновые уравнения вида (9.2). Таким образом, все характеристики свободного электромагнитного поля подчиняются волновым уравнениям. 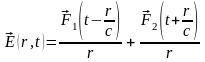, (9.3)

где - произвольные функции. Первое слагаемое описывает электромагнитную волну, которая распространяется со скоростью 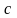вдоль радиус-вектора 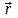, и амплитуда которой убывает с расстоянием по закону (расходящаяся сферическая волна). Второе слагаемое описывает волну, распространяющуюся в противоположном направлении (сходящаяся сферическая волна). Электрическое и магнитное поля в плоской электромагнитной волне изменяются в пространстве и во времени синфазно. Электромагнитная волна является поперечной волной: векторы 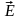и лежат в плоскости перпендикулярной направлению распространения волны, перпендикулярны друг другу и их модули равны.

Все данные свойства справедливы и для сферических волн.

• линейная — колебания возмущения происходит в какой-то одной плоскости. В таком случае говорят о «плоско-поляризованной волне»;

• круговая — конец вектора амплитуды описывает окружность в плоскости колебаний. В зависимости от направления вращения вектора может быть правой или левой.

На основе этих двух или только круговой можно сформировать и другие, более сложные виды поляризации. Например, эллиптическая. В общем случае, круговая поляризация — вещь теоретическая, на практике же говорят об эллиптической поляризации — с левым или правым направлением вращения.

Гармонической волной называется линейная монохроматическая волна Степенью поляризации называется величина

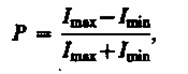   где I_max и I_min, - соответственно максимальная и минимальная интенсивности частично поляризованного света, пропускаемого анализатором. Для естественного света I_max = I_min и Р = 0, для плоскополяризованного I_min = 0 и Р = 1.