1) Определение

Базовыми элементами, которыми оперирует алгебра логики, являются высказывания. Высказывания строятся над множеством {B,  ,  ,  , 0, 1}, где B — непустое множество, над элементами которого определены триоперации:

 отрицание (унарная операция),

 конъюнкция (бинарная),

 дизъюнкция (бинарная),

а также константы — логический ноль 0 и логическая единица 1.

Дизъю́нкт — пропозициональная формула, являющаяся дизъюнкцией одного или более литералов (например  ). Конъюнкт — пропозициональная формула, являющаяся конъюнкцией одного или более литералов (например  ).

[Править]Аксиомы

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

[Править]Логические операции

Простейшим и наиболее широко применяемым примером такой алгебраической системы является множество B, состоящее всего из двух элементов:

B = { Ложь, Истина }

Как правило, в математических выражениях Ложь отождествляется с логическим нулём, а Истина — с логической единицей, а операции отрицания (НЕ), конъюнкции (И) и дизъюнкции (ИЛИ) определяются в привычном нам понимании. Легко показать, что на данном множестве B можно задать четыре унарные и шестнадцать бинарных отношений и все они могут быть получены через суперпозицию трёх выбранных операций.

Опираясь на этот математический инструментарий, логика высказываний изучает высказывания и предикаты. Также вводятся дополнительные операции, такие как эквивалентность   («тогда и только тогда, когда»), импликация   («следовательно»), сложение по модулю два   («исключающее или»), штрих Шеффера  , стрелка Пирса   и другие.

Логика высказываний послужила основным математическим инструментом при создании компьютеров. Она легко преобразуется в битовую логику: истинность высказывания обозначается одним битом (0 — ЛОЖЬ, 1 — ИСТИНА); тогда операция   приобретает смысл вычитания из единицы;   — немодульного сложения; & — умножения;   — равенства;   — в буквальном смысле сложения по модулю 2 (исключающее Или — XOR);   — непревосходства суммы над 1 (то есть A   B = (A + B) <= 1).

Впоследствии булева алгебра была обобщена от логики высказываний путём введения характерных для логики высказываний аксиом. Это позволило рассматривать, например, логику кубитов, тройственную логику (когда есть три варианта истинности высказывания: «истина», «ложь» и «не определено») и др.

[Править]Свойства логических операций

1. Коммутативность: x y = y x,  {&,  }.

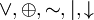2. Идемпотентность: x x = x,  {&,  }.

3. Ассоциативность: (x y) z = x (y z),  {&,  }.

4. Дистрибутивность конъюнкций и дизъюнкции относительно дизъюнкции, конъюнкции и суммы по модулю два соответственно:

   • ,

   • ,

   • .

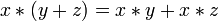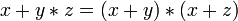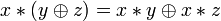5. Законы де Мо́ргана:

   • ,

   • .

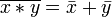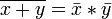6. Законы поглощения:

   • ,

   • .

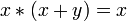7. Другие (1):

   • .

   • .

   • .

   • .

   • .

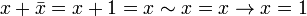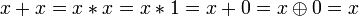8. Другие (2):

   • .

   • .

   • .

   • 

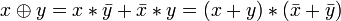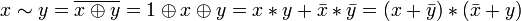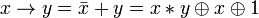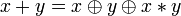
9. Другие (3) (Дополнение законов де Мо́ргана):

   • .

   • .

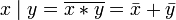Существуют методы упрощения логической функции: например, Карта Карно, метод Куайна - Мак-Класки

2) Понятие системы охватывает комплекс взаимосвязанных элементов, действующих как единое целое. Система включает в себя следующие компоненты:

Свойства информационных систем.

Свойство относительности устанавливает, что состав элементов, взаимосвязей, выходов, входов, целей и ограничений зависит от целей исследования. Реальный мир на много богаче проектируемой системы, поэтому исследователю требуется определить, какие из сторон реального мира будут охватывать его система. При выделении системы некоторые элементы, взаимосвязи, входы, выходы не включаются в систему из-за слабого влияния на остающиеся элементы, из-за самостоятельных целей, которые могут плохо согласовываться со всей системой. Они образуют внешнюю среду ИС.

Делимость означает, что систему можно представить состоящей из относительно самостоятельных частей (подсистем), каждая из которых может рассматриваться как система. Возможность выделения подсистем или декомпозиция системы упрощает ее анализ, т. к. число взаимосвязей между подсистемами и внутри них обычно меньше, чем число связей непосредственно между всеми элементами системы. См. рис. 2, где 1— учет кредиторов, 2 — учет кредитов, 3 — учет денежных средств. Деление на подсистемы условно и не всегда обязательно. Декомпозиция производится по желанию исследователя.

Свойство целостности. Подразумевает согласованность целей функционирования всей системы с целями функционирования ее подсистем и элементов. Также нельзя забывать, что при декомпозиции системы она теряет ряд своих свойств.

Системы информационного обеспечения.

12

1) Понятие алгоритма — одно из основных в программировании и информатике^[1]. Это последовательность команд, предназначенная исполнителю, в результате выполнения которой он должен решить поставленную задачу. Алгоритм должен описываться на формальном языке, исключающем неоднозначность толкования. Исполнитель может быть человеком или машиной. Исполнитель должен уметь выполнять все команды, составляющие алгоритм. Множество возможных команд конечно и изначально строго задано. Действия, выполняемые по этим командам, называются элементарными.

Запись алгоритма на формальном языке называется программой. Иногда само понятие алгоритма отождествляется с его записью, так что слова «алгоритм» и «программа» — почти синонимы. Небольшое различие заключается в том, что под алгоритмом, как правило, понимают основную идею его построения. Программа же всегда связана с записью алгоритма на конкретном формальном языке.

2) Информационная система — это взаимосвязанная совокупность средств, методов и персонала, используемых для хранения, обработки и выдачи информации для достижения цели управления. В современных условиях основным техническим средством обработки информации является персональный компьютер. Большинство современных информационных систем преобразуют не информацию, а данные. Поэтому часто их называют системами обработки данных.

По степени механизации процедур преобразования информации системы обработки данных делятся на системы ручной обработки, механизированные, автоматизированные и системы автоматической обработки данных.

Важнейшими принципами построения эффективных информационных систем являются следующие.

Принцип интеграции, заключающийся в том, что обрабатываемые данные, однажды введенные в систему, многократно используются для решения большого числа задач.

Принцип системности, заключающийся в обработке данных в различных аспектах, чтобы получить информацию, необходимую для принятия решений на всех уровнях управления.

Принцип комплексности, заключающийся в механизации и автоматизации процедур преобразования данных на всех этапах функционирования информационной системы.

Информационные системы также классифицируются:

по функциональному назначению: производственные, коммерческие, финансовые, маркетинговые и др.;

по объектам управления: информационные системы автоматизированного проектирования, управления технологическими процессами, управления предприятием (офисом, фирмой, корпорацией, организацией) и т. п.;

по характеру использования результатной информации: информационно-поисковые, предназначенные для сбора, хранения и выдачи информации по запросу пользователя; информационно-советующие, предлагающие пользователю определенные рекомендации для принятия решений (системы поддержки принятия решений); информационно-управляющие, результатная информация которых непосредственно участвует в формировании управляющих воздействий.

Структуру информационных систем составляет совокупность отдельных ее частей, называемых подсистемами.

Функциональные подсистемы реализуют и поддерживают модели, методы и алгоритмы получения управляющей информации. Состав функциональных подсистем весьма разнообразен и зависит от предметной области использования информационной системы, специфики хозяйственной деятельности объекта, управления.

В состав обеспечивающих подсистем обычно входят:

информационное обеспечение — методы и средства построения информационной базы системы, включающее системы классификации и кодирования информации, унифицированные системы документов, схемы информационных потоков, принципы и методы создания баз данных;

техническое обеспечение — комплекс технических средств, задействованных в технологическом процессе преобразования информации в системе. В первую очередь это вычислительные машины, периферийное оборудование, аппаратура и каналы передачи данных;

программное обеспечение включает в себя совокупность программ регулярного применения, необходимых для решения функциональных задач, и программ, позволяющих наиболее эффективно использовать вычислительную технику, обеспечивая пользователям наибольшие удобства в работе;

математическое обеспечение — совокупность математических методов, моделей и алгоритмов обработки информации, используемых в системе;

лингвистическое обеспечение — совокупность языковых средств, используемых в системе с целью повышения качества ее разработки и облегчения общения человека с машиной.

Организационные подсистемы по существу относятся также к обеспечивающим подсистемам, но направлены в первую очередь на обеспечение эффективной работы персонала, и поэтому они могут быть выделены отдельно. К ним относятся:

кадровое обеспечение — состав специалистов, участвующих в создании и работе системы, штатное расписание и функциональные .обязанности;

эргономическое обеспечение — совокупность методов и средств, используемых при разработке и функционировании информационной системы, создающих оптимальные условия для деятельности персонала, для быстрейшего освоения системы;

правовое обеспечение — совокупность правовых норм, регламентирующих создание и функционирование информационной системы, порядок получения, преобразования и использования информации;

организационное обеспечение — комплекс решений, регламентирующих процессы создания и функционирования как системы в целом, так и ее персонала.

13

1) Из многообразия всевозможных алгоритмов выделяются три основных типовых структуры:

линейная,

разветвляющаяся,

циклическая.

Линейным называется алгоритм, в котором всегда выполняются все действия строго последовательно.

Как правило, алгоритмы линейной структуры состоят из трех частей: ввод исходных данных, вычисления результатов по формулам, вывод значений результатов. Это самые простые алгоритмы.

ПРИМЕР 1. Найти сторону и диагональ квадрата, если известна его площадь.

Разветвляющимся называется алгоритм, при выполнении которого каждый раз последовательность действий может быть разная, т.е. каждый раз выбирается один из нескольких путей прохождения схемы алгоритма. Конкретный путь прохождения алгоритма называется ветвью алгоритма. Схема подобного алгоритма обязательно содержит хотя бы один блок (символ) "решение", который и обеспечивает разветвление вычислительного процесса.

ПРИМЕР 2. Вычислить значение функции y по формуле

 .

Циклическим называется алгоритм, который содержит участок, выполняющийся многократно, каждый раз с новыми значениями переменных, изменяющихся по одним и тем же законам. По способу организации циклы делятся на два основных вида:

• циклы с известным заранее числом повторений (классические);

• циклы с неизвестным числом повторений (итерационные).

Классический цикл организуется с помощью специальной переменной, которая называется параметром цикла.  Параметр цикла - это числовая переменная, которая управляет работой цикла. Она изменяется по закону арифметической прогрессии, что обеспечивает повторение цикла нужное количество раз. Для этого заранее должны быть известны:

начальное значение параметра (обозначим его    );

конечное значение параметра (обозначим его    );

• шаг изменения параметра (обозначим его   ).

 

Зная эти 3 величины, можно вычислить количество повторений цикла по формуле:          

2) Из всех позиционных систем особенно проста двоичная система счисления. Рассмотрим выполнение основных арифметических действий над двоичными числами. 

     Все позиционные системы счисления "одинаковы”, а именно, во всех них выполняются арифметические операции по одним и тем же правилам:

• справедливы одни и те же законы арифметики: коммутативный, ассоциативный, дистрибутивный;

• справедливы правила сложения, вычитания и умножения столбиком;

• правила выполнения арифметических операций опираются на таблицы сложения и умножения.

Сложение

 

Рассмотрим примеры на сложение. 

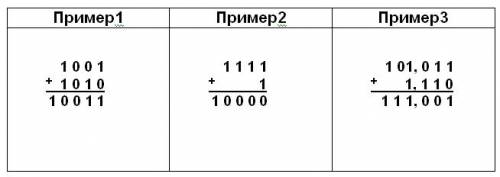
     При сложении столбиком двух цифр справа налево в двоичной системе счисления, как в любой позиционной системе, в следующий разряд может переходить только единица.

     Результат сложения двух положительных чисел имеет либо столько же цифр, сколько у максимального из двух слагаемых, либо на одну цифру больше, но этой цифрой может быть только единица.

Вычитание

 

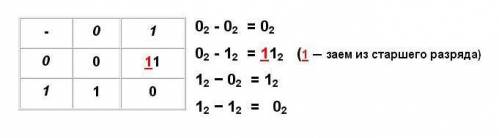
     Рассмотрим примеры  на вычитание.        При выполнении операции вычитания всегда из большего по абсолютной величине числа вычитается меньшее и у результата ставится соответствующий знак. Умножение       Рассмотрим примеры  на умножение.      Операция умножения выполняется с использованием таблицы умножения по обычной схеме (применяемой в десятичной системе счисления) с последовательным умножением множимого на очередную цифру множителя. Рассмотрим примеры  на умножение.      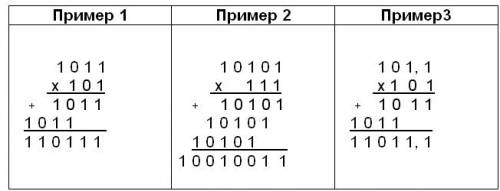При выполнении умножения в примере 2 складываются три единицы 1+1+1=11 в соответствующем разряде пишется 1, а другая единица переносится в старший разряд. В двоичной системе счисления операция умножения сводится к сдвигам множимого и сложению промежуточных результатов. Деление      Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной системе счисления.      Рассмотрим примеры на деление

14