10. Вычисление криволинейного интеграла I рода: явное представление кривой, параметрическое представление кривой, полярное представление кривой.

2.2. Вычисления криволинейного интеграла I рода

Вычисление КРИ-I может быть сведено к вычислению определенного интеграла. Приведем без доказательства формулы вычисления КРИ-I в случаях, если кривая задана явным образом, параметрически и в полярных координатах.

Явное представление кривой

Если плоская кривая задана непрерывной и непрерывно дифференцируемой на функцией , где и  соответственно абсциссы точек и , то

. (2.3)

Параметрическое представление кривой

Если кривая задана параметрически уравнениями , где и  непрерывно дифференцируемые функции параметра , причем точке соответствует значение , а точке  значение , то

. (2.4)

В случае если гладкая кривая задана в пространстве параметрическими уравнениями , то

.

Полярное представление кривой

Если плоская кривая задана уравнением , причем функция и ее производная непрерывны, то имеет место следующая формула

. (2.5)

Пример 2.1. Вычислить интеграл , где  отрезок прямой, заключенный между точками и .

Решение. Составляем уравнение по двум точкам. Получаем .

Находим

.

Следовательно,

.

Пример 2.2. Вычислить интеграл , где  лепесток лемнискаты расположенный в первом координатном углу.

Решение. Находим .

.

16. Приложения кри-I кри-2.

Некоторые приложения криволинейного интеграла I рода

Криволинейный интеграл I рода имеет разнообразные приложения в математике и механике.

Длина кривой

Длина кривой , плоской или пространственной линии, вычисляется по следующей формуле

.

Площадь цилиндрической поверхности

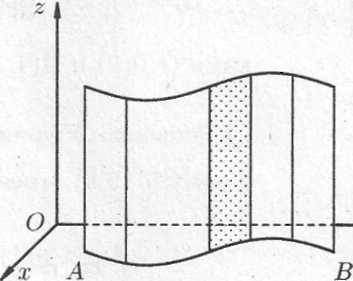
Если направляющей цилиндрической поверхности служит кривая , лежащая в плоскости , а образующая параллельная оси (см. рисунок), то площадь поверхности, заданной функцией , находится по формуле:

Масса кривой

Если  плотность материальной кривой (провод, цепь, трос, …), то ее масса вычисляется по формуле:

.

Координаты центра масс

Координаты центра масс материальной дуги , имеющей плотность , определяются по формулам:

; ; .

Моменты инерции

Моменты инерции относительно начала координат , осей координат и , и координатных плоскостей и материальной дуги , имеющей плотность , определяются по формулам:

;

, , ;

, , .

Пример 2.3. Вычислить массу и координаты центра масс плоской материальной дуги , плотность которой .

Решение. Согласно формуле (2.3) и формуле массы кривой, для случая плоской дуги имеем:

.

Согласно формулам координат центра масс, получаем:

.

.

Некоторые приложения криволинейного интеграла II рода

Площадь плоской фигуры

Площадь плоской фигуры, расположенной в плоскости и ограниченной замкнутой линией , можно найти по формуле

,

при этом кривая , делает обход против часовой стрелки.

Работа переменной силы

Переменная сила на криволинейном участке производит работу, которая находится по формуле

.

Пример 2.6. Найти работу силы вдоль кривой от точки до точки .

Решение. По формуле работы переменной силы находим

.