7.Механические приложения двойного интеграла.

Масса плоской фигуры

Согласно физическому смыслу двойного интеграла, масса плоской пластины находится по формуле:

,

где  плотность этой пластины.

Статистические моменты плоской фигуры

Статистические моменты плоской фигуры относительно осей и могут быть вычислены по формулам:

;

.

Координаты центра масс

Координаты плоской фигуры вычисляются по следующим формулам:

;

.

Моменты инерции плоской фигуры

Моментом инерции материальной точки массы относительно оси называется произведение массы на квадрат расстояния точки до оси, т.е. .

Моменты инерции плоской фигуры относительно осей и могут быть вычислены по формулам:

;

.

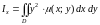Момент инерции плоской фигуры относительно начала координат вычисляется по следующей формуле:

.

Пример 1.5. Дана неоднородная пластина , ограниченная линиями , , с поверхностной плотностью . Вычислить:

1) массу плоской пластины;

2) статистические моменты и пластины относительно осей координат;

3) координаты центра масс пластины;

4) моменты инерции относительно начало координат и осей координат .

8 Вычисление и свойство тройного интеграла.

Теория тройного интеграла аналогична теории двойного интеграла.

Рассмотрим в пространстве замкнутую область . Пусть в области задана непрерывная функция .

Схема получения тройного интеграла

1) Разбиваем область на «элементарных областей» .

2) Объем «элементарной области» обозначим , а диаметр (наибольшее расстояние между двумя точками области) – через .

3) Возьмем произвольную точку .

4) Находим .

5) Составляем интегральную сумму

.

6) Обозначим через длину наибольшего из диаметров «элементарных областей», т.е. , . Найдем предел интегральной суммы, когда так, что .

.

Предел интегральной суммы, когда число «элементарных областей» неограниченно возрастает, а длина наибольшего диаметра стремится к нулю, называется тройным интегралом от на замкнутой областью .

Таким образом, тройным интегралом от по замкнутой областью называется предел интегральной суммы , когда число «элементарных областей» неограниченно возрастает, а длина наибольшего диаметра стремится к нулю:

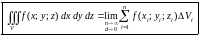. (1.7)

 интегрируемая функция в области ;

 область интегрирования;

, и  переменные интегрирования;

или  элемент объема.

Основные свойства тройного интеграла

Тройной интеграл обладает теми же свойствами, что и двойной интеграл.

1. Если в области f(xyz) =_, То 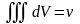, где v- объём области V

2. В случае, когда подынтегральная функция f(xyz) задаёт плотность δ(x,y,z) тела, занимающего область V, тройной интеграл выражает массу этого тела:

m= δ(x,y,z)dV

9.Вычисление тройного интегралав декартовых координатах

В декартовых координатах вычисление тройного интеграла водится к последовательному вычислению трех определенных интегралов.

прямая, параллельная оси , пересекает границу области не более чем в двух точках.

Для правильной области справедливы следующие неравенства:

, , .

Тогда тройной интеграл в декартовых координатах вычисляется по следующей формуле:

. (1.8)

Таким образом, при вычислении тройного интеграла в случае простейшей правильной области вначале интегрируют функцию по одной из переменных (например, ) при условии, что оставшиеся две переменные принимают любые постоянные значения в области интегрирования, затем результат интегрируют по второй переменной (например, ) при любом постоянном значении третьей переменной в и, наконец, выполняют интегрирование по третьей переменной (например, ) в максимальном диапазоне ее изменения в . Надо отметить, что порядок интегрирования в формуле (1.8), при определенных условиях, может быть другим.

Если область более сложная, чем рассматриваемая, то ее следует разбить на конечное число таких областей (правильных), к которым можно применить формулу (1.8).

Пример 1.6. Вычислить тройной интеграл

,

где область ограничена поверхностями: .

Решение. По заданным поверхностям строим область интегрирования:  плоскости,  эллиптический параболоид.

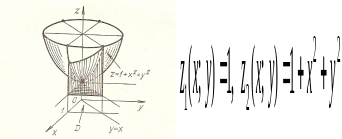
Тогда

.

,
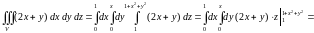
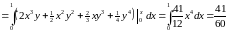