3 Вычисление двойного интеграла в полярных координатах

4 Двойной интеграл в криволинейных координатах.

При вычислении определенного интеграла важную роль играет правило замены переменной, согласно которому при соблюдении соответствующих условий получаем

.

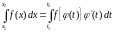Обычно функция монотонна. Она осуществляет взаимно однозначное соответствие между точками промежутка изменения переменной и точками промежутка изменения переменной . Делая замену по формуле , необходимо заменить на и вместо старых пределов и по переменной взять им соответствующие новые пределы и по переменной .

Для упрощенного вычисления двойного интеграла также применяется метод подстановки. Но правило замены переменной в двойном интеграле значительно сложнее, чем в определенном интеграле. Приведем только окончательную формулу замены переменных в двойном интеграле и разъясним ее на примере преобразования к полярным координатам.

Определим преобразование независимых переменных и как

и .

Если функции и имеют в некоторой области плоскости непрерывные частные производные первого порядка и отличный от нуля определитель

,

а функция непрерывна в области , то справедлива формула замены переменной в двойном интеграле:

. (1.4)

Сами новые переменные и называются криволинейными координатами. Различные системы криволинейных координат играют важную роль в математике и ее приложениях.

Функциональный определитель называется определителем Якоби или якобианом (Г. Якоби (1804 – 1851) – немецкий математик).

Рассмотрим частный случай замены переменных, часто используемый при вычислении двойного интеграла, а именно замену декартовых координат и полярными координатами и .

В качестве переменных и возьмем полярные координаты и . Они связаны с декартовыми координатами формулами , .

Правые части в этих равенствах – непрерывно дифференцируемые функции. Якобиан преобразования определяется как

Формула замены переменных (1.4) принимает вид:

, (1.5)

где  область в полярной системе координат, соответствующая области в декартовой системе координат.

пересекает ее границу не более чем в двух точках. Тогда правую часть формулы (1.5) можно записать в виде повторного интеграла

. (1.6)

Внутренний интеграл берется при постоянном . Формула (1.6) применяется, если полюс 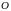полярной системы координат находится вне области . В отдельных случаях формула (1.6) упрощается.

Пример 1.2. Вычислить , если область  круг .

Решение. Если область  круг или его часть, то интеграл проще вычислить в полярных координатах. Вводим замену: , . Тогда , . Область так же запишем в полярных координатах: или . Поскольку полюс находится внутри области , то , , 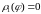и . Согласно формуле (1.6) имеем .

5 Вычисление объёмов тел площадей плоских фигур с помощью двойного интеграла.

Объем тела

Согласно геометрическому смыслу двойного интеграла, объем цилиндрического тела находится по формуле:

,

где  уравнение поверхности, ограничивающей тело сверху.

Площадь плоской фигуры

Согласно свойству 6 двойного интеграла, если , то цилиндрическое тело «превращается» в прямой цилиндр с высотой, равной 1. Объем такого цилиндра численно равен площади основания , т.е. площади области интегрирования . Тогда для вычисления площади плоской фигуры получаем формулы:

1. для вычисления в декартовой системе координат: ;

2. для вычисления в полярной системе координат: .

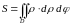Пример 1.3. Найти площадь фигуры, ограниченной линиям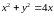и , , и .

Решение. Построим в декартовой системе координат фигуру .

, а прямая  .

Согласно формуле (1.6) имеем

.

,

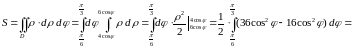
Пример 1.4. С помощью двойного интеграла найти объем тела, ограниченного данными поверхностями: .

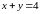Решение. Данное тело сверху ограничено поверхностью  параболическим цилиндром, снизу плоскостью , с боков плоскостями и . Чтобы найти объем тела, изобразим область в плоскости .

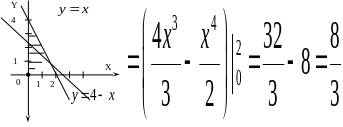
6. Вычисление площадей поверхностей с помощью двойного интеграла.

Вычисление площади плоской фигурыПлощадь плоской фигуры, ограниченной областью D, находится по формуле . (105)Если область определена в прямоугольной системе координат неравенством  , то из (105) имеем . (106)Если область D определена в полярных координатах неравенством  ,  , то . (107)

Вычисление площади пространственных поверхностейЕсли гладкая однозначная поверхность задана уравнением z = f (x,y),то площадь этой поверхности выражается формулой , (108)где D есть проекция данной поверхности на плоскость хОу.Если поверхность задана уравнением x = f (y, z),то для вычисления площади имеем аналогичную формулу . (109)Однако здесь D есть проекция поверхности на плоскость yOz.Аналогично, если поверхность задана уравнением y = f (x, z), , (110)где D – проекция поверхности на плоскость xOz.

,