РГР

Национальный исследовательский университет

«Московский институт электронной техники»

Кафедра: ВМ-1

Дисциплина: Численные методы

Расчётно-графическая работа

«Интерполяция многочленами Эрмита»

Руководитель:

Ярошевич Владимир Александрович

Выполнила

студентка группы МП-22А

Шкурко Мария Алексеевна

Москва

2018

Теоретические сведения

Постановка задачи и основные понятия

В узлах 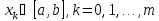, среди которых нет совпадающих узлов, заданы значения функции и её производных 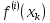до порядка 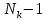включительно, i = 1, 2, …, 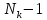. Таким образом, в каждой точке 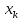, k = 0, 1, …, m, известны

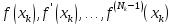
и, следовательно, всего известно 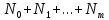величин. Требуется алгебраический многочлен 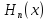степени n =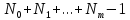, для которого

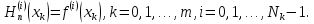(1)

Многочлен 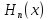, удовлетворяющий условиям (1), называется интерполяционным многочленом Эрмита для функции f(x). Число 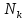называется кратностью узла .

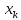(2)

Алгоритм

Даны несовпадающие узлы 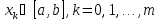и их кратности 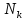. Задана функция f(x).

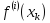1. Находим значения функции и её производных до порядка 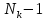включительно, i = 1, 2, …, .

2. Вычисляем 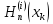по формуле (1).

3. Составляем систему из n уравнений по формуле (2) и её производным до 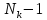порядка, подставляя узлы 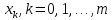и вычисленные на втором шаге .

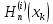4. Находим из системы коэффициенты .

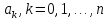5. Подставляем найденные коэффициенты в (1).

Реализация алгоритма в среде Matlab

function [a,p] = Hermit(X,N)

%X - вектор узлов

%N - вектор кратностей узлов

%p - степень многочлена Эрмита

k = length(X);

n = sum(N);

p = n - 1;

F = fun(X);

m = max(N)-1;

%оптимальный шаг

x = X(1)-10^-3:10^-3:X(k)+10^-3;

f = fun(x);

d2f = diff(f,m)/(10^-3)^m;

h = m*sqrt(2^(-52)/max(abs(d2f)));

df = zeros(1,n-k);

A1 = ones(k,n);

A2 = zeros(n-k,n);

for i = 2:1:n

A1(:,i) = X'.^(i-1);

end

index = 1;

str = 1;

for i = 1:1:k

if (N(i) ~= 1)

for j = 2:1:N(i)

df(index) = DF_X(X(i),h,j-1);

index = index + 1;

st = 0;

for t = j:1:n

if (j == 2)

A2(str,t) = (st+1)*X(i)^st;

st = st + 1;

else

A2(str,t) = (st+1)*A2(str-1,t)/X(i);

st = st + 1;

end

end

str = str + 1;

end

end

end

A = [A1; A2];

H1 = [F'; df'];

a = A\H1;

end

function df = DF_X(x0,h,n)

X = zeros(1,n+1);

X(1) = x0;

for i = 2:1:n+1

X(i) = X(i-1)+h;

end

F = fun(X);

df = diff(F,n)/h^n;

end

function f = fun(x)

f = 3*x.^3 - 4*x.^2 + x - 5;

end

>> X = [-1, 0, 1];

>> N = [1,2,1];

>> [a,p]=Hermit(X,N)

a =

-5.0000

1.0000

-4.0000

3.0000

p = 3