2. Преобразование Фурье. Ряд Фурье

Бесконечный периодический сигнал , удовлетворяющий заданным требованиям, можно разложить в ряд Фурье.

Ряд Фурье позволяет вычислить дискретные значения спектра сигнала, называемые гармониками сигнала: , , . Под спектром сигнала подразумевается совокупность амплитуд и фаз гармонических сигналов в разложении исходного сигнала в ряд Фурье. Таким образом, спектр сигнала является функцией амплитуды и фазы от частоты. На практике различают амплитудный и фазовый спектры.

Ряд Фурье представляется в следующем виде:

.

Коэффициенты ряда , и вычисляются по следующим формулам:

,

,

.

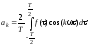Частные суммы ряда могут быть представлены в виде

,

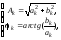
где - амплитуда гармоники с номером k в спектре сигнала; - фаза гармоники с номером k в спектре сигнала. При этом спектр сигнала является дискретным.

3. Интеграл Фурье

Если сигнал непериодический, то для вычисления спектра сигнала используется интеграл Фурье:

;

Коэффициенты 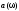и вычисляются по следующим формулам:

;

;

При этом спектр сигнала является непрерывным.

4. Расширение непериодического сигнала конечной длительности до периодического сигнала бесконечной длительности

Рассмотрим функцию с периодом , . Построим непериодическую функцию:

Заметим, что .

При , выполняется равенство:

, (1)

где 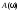значение спектра функции 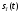, амплитуда гармоники с номером в спектре .

5. Логарифмические единицы для измерения амплитуды и мощности

На практике для измерения амплитуды и мощности 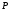сигналов принято использовать логарифмические единицы:

, (2)

,

где 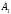- амплитуда гармонического сигнала, принимаемого за единицу отсчета.

При использовании логарифмических единиц отношение амплитуд или мощностей двух сигналов, выраженное в децибелах, может быть вычислено как разность амплитуд или мощностей сигналов, выраженных в децибелах:

;

В практике частотного анализа сигналов распространены единицы, производные от децибел: децибел-вольты () - единицы измерения, численно равные значению сигнала в децибелах по отношению к сигналу, имеющему действующее значение 1В.

Таким образом, амплитуда синусоидального сигнала, выраженная в децибел-вольтах, равна .

6. Взаимосвязь спектра конечного непериодического и расширенного бесконечного периодического сигнала

Комбинируя выражения (1) и (2) получаем следующее равенство:

Таким образом, можно использовать разложение функции в ряд Фурье для вычисления значений спектра функции при .

7. Быстрое преобразование Фурье

Быстрое преобразование Фурье (БПФ) - это алгоритм вычисления дискретного преобразования Фурье при количестве отсчетов сигнала, равном степени двойки.

Дискретное преобразование Фурье (ДПФ) - дискретизованная функция непрерывного преобразования Фурье, которая вычисляется для дискретизованного по времени сигнала.

Одной из дополнительных возможностей современных цифровых осциллографов является возможность вычисления спектра сигнала. В цифровом осциллографе спектр сигнала вычисляется для той части сигнала, которая изображается на экране осциллографа. Для вычисления спектра сигнала цифровой осциллограф использует алгоритм БПФ.

1. Частота спектра, расположенная по центральной линии;

2. Вертикальная шкала в дБ на деление (0 дБ = 1/ В)

3. Горизонтальная шкала по частоте на деление;

4. Частота выборки;

5. Тип используемого окна в алгоритме БПФ.