Курсовая работа онх

Российский химико-технологический университет

имени Д. И. Менделеева

Кафедра общей и неорганической химии

Курсовая работа

Нахождение физико-химических величин на основе

методов сравнительного расчёта М. Х. Карапетьянца

Подготовила: Новикова Полина

Группа ПР – 11, курс 1

Факультет ИПУР

Преподаватель: Ахапкина Т. Е.

При выполнении полученного задания постройте график линейной зависимости y=a+bx. Используя один из методов сравнительного расчёта М. Х. Карапетьянца, определите искомую величину графическим способом и аналитическим.

Задание 19.

Определить молярную теплоёмкость кристаллического нитрата стронция при 298,15К С_{р, 298} если нитраты элементов IIА-подгруппы Периодической системы элементов Д. И. Менделеева характеризуются следующими значениями С_{р, 298} (у) и стандартной энтропии S°₂₉₈ (х):

Ме(NO3)2	Mg(NO3)2	Ca(NO3)2	Sr(NO3)2	Ba(NO3)2
Cp, 298к, Дж/(моль × К)	143	149	?	152
S0298k, Дж/(моль × К)	167	194	195	213

1 метод:

На Рис. 1 представлен график зависимости молярной теплоемкости от стандартной энтропии нитратов металлов IIА-подгруппы Периодической системы элементов Д. И. Менделеева. С помощью линии тренда определено уравнение линейной зависимости - y = 0,1974x + 110,22

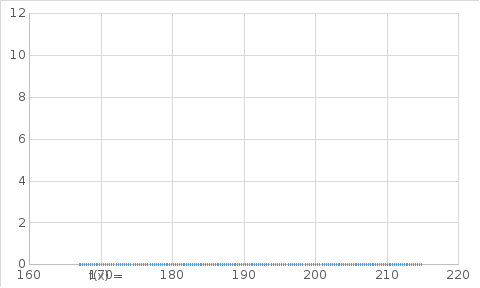Рис. 1

Подставив известное нам значение x в уравнение, находим значение y.

Y=0,1974×195 + 110,22 = 148,713 ≈ 149

Ответ: 149 Дж/(моль × К)

2 метод(метод наименьших квадратов):

Этот метод дает возможность при заданном типе зависимости функции 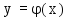так выбрать ее числовые параметры, чтобы кривая графика функции наилучшим образом отображала экспериментальные данные. Часто из физических соображений, связанных с существом решаемой задачи, вид зависимости(в нашем случае – линейный) бывает известен; из опыта требуется только установить числовые параметры этой зависимости.

Когда вид функции сглаживания выбран, задача сводится к нахождению параметров выбранной функции сглаживания, чтобы она наилучшим образом изображала зависимость, полученную в результате эксперимента. Решение этой задачи зависит от того, что именно мы условимся считать «наилучшим». При использовании метода наименьших квадратов требование наилучшего согласия выбранной аппроксимацией кривой 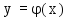экспериментальными данными сводится к тому, чтобы сумма квадратов отклонений экспериментальных точек от сглаживающей кривой обращалась в минимум

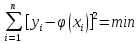
Функция 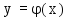– функция не только аргумента x, но и числовых параметров a, b, c… Таким образом, нам нужно, чтобы выполнялось следующее условие:

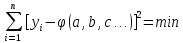
Найдем значения переменных параметров, обратив левую часть уравнения в минимум. Для это продифференцируем выражение по данным переменным и приравняем производную к нулю.

Где 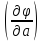– значение частной производной функции y=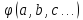 по параметру a в точке x₁ и так далее. Система уравнений содержит столько уравнений, сколько существует неизвестных параметров. Систему в общем виде решить нельзя, для ее решения необходимо задать конкретный вид функции

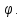
Если функция, для которой осуществляется подбор параметров, линейная, то она имеет вид:

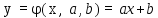
В таком случае можно получить аналитические выражения для параметров :

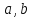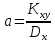
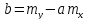
Где основные числовые характеристики анализируемого распределения выражаются:

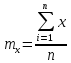– математическое ожидание значения величины x

- математическое ожидание значения величины y

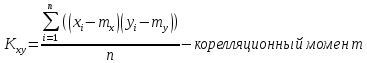
Для определения известной величины С_р,298К для нитрата стронция необходимо найти коэффициенты a и b в уравнении вида:

С_р,298К = a×S⁰_298K + b

Для этого воспользуемся данными таблицы и аналитическим методом наименьших квадратов.

С_р,298К (средняя) =

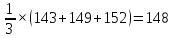
S⁰_298K (средняя) =

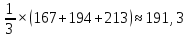
К_{Ср, 298К; S}⁰_298K =

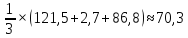
D_x =

a=

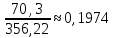
b=

Следовательно, исходное уравнение будет иметь вид:

С_р,298К = 0,1974× S⁰_298K + 110,23

Подставим известную величину для нитрата стронция в уравнение:

С_р,298К = 148, 723 ≈ 149

Ответ: 149 Дж/(моль × К)

3 метод: Построение графической зависимости с помощью миллиметровой бумаги. Нахождение неизвестной величины методом графической экстраполяции. (см. стр 5)

Выводы:

1) Аналитическим и графическим методами была определена стандартная энтропия образования нитрата стронция с помощью методов сравнительного расчета Карапетьянца.

2) Самым точным я считаю метод наименьших квадратов, так как именно этот метод позволяет найти значения коэффициентов с точностью до десяти тысячных долей, а результат – с точностью до тысячных. Однако, в этом методе проводится множество расчетов, при которых возрастает шанс случайной ошибки. Метод графической экстраполяции считаю наименее точным, так как здесь имеет место быть человеческий фактор и другие приборные погрешности(толщина стержня карандаша и т.д.). Таким, образом метод построения графика в Excel считаю самым точным для проведения сравнительного анализа.

Москва 2019