7. Расчет привода с ременной передачей и коническо-цилиндрическим редуктором

7.1.Расчет конической передачи

По кинематической схеме привода определить параметры коническо-цилиндрического редуктора (рис. 9).

Материал зубчатых колес Сталь 40ХН, термообработка – улучшение и закалка ТВЧ до твердости HRC 48....53 [2].

Время работы передачи при коэффициенте суточного использования К_сут = 0,7 и годового использования К_год =0,8.

Время работы передачи:

,

где k – срок службы привода.

Число циклов перемены напряжений для колеса:

,

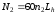для шестерни: .

Число циклов напряжений при расчете по контактным напряжениям:

Коэффициенты долговечности по контактным напряжениям.

N₁N_HO,тоK_HL1=1; N₂N_HO,тоK_HL2=1

Рис. 9. Кинематическая схема привода

с коническо-цилиндрическим редуктором: 1 – электродвигатель;

2 – ременная передача; 3 – коническо-цилиндрический редуктор;

4 – муфта фрикционная

Базовое контактное напряжение:

– для шестерни;

– для колеса.

Допускаемое контактное напряжение:

.

Базовое число циклов перемены напряжений при изгибе:

N_FO=410⁶.

Коэффициенты долговечности при расчете по изгибу:

N₁N_FO,тоK_FL1=1,

N₂N_FO, тоK_FL2=1.

Допускаемые напряжения при изгибе:

.

7.1.1 Расчет геометрических параметров колес

Геометрические параметры передачи показаны на рис.11.

Пример вал шестерни конической приведен в приложении 16.

Рис.10. Геометрические параметры передачи

Диаметр внешней делительной окружности колеса:

,

где v_H= 1 – для прямозубых колес;

v_H=1,85 – для колес с круговым зубом;

K_Hv=1,2 – коэффициент, учитывающий внутреннюю динамику нагрузки для прямозубых колес с твердостью больше 350HB;

K_Hβ=1+2_bd/S – коэффициент неравномерности распределения нагрузки по длине контактных линий, а – коэффициент ширины, S=2 – индекс схемы (см. рис. 12).

Углы делительные конусов:

,

.

Конусное расстояние:

.

Ширина колес:

.

Модуль передачи:

,

где K_Fβ= 1 – коэффициент неравномерности распределения нагрузки по длине контактных линий при изгибе для прямозубых колес;

K_Fβ=1,08 – для колес с круговым зубом;

v_F=0,85 – для прямозубых колес;

v_F= 1 – для колес с круговым зубом.

Число зубьев:

колеса ; шестерни .

Фактическое передаточное число

.

Отклонение от заданного числа не должно быть больше 4 %

Окончательные значения размеров колес.

Углы делительных конусов колеса и шестерни:

;.

Делительные диаметры колес:

,

.

Внешние диаметры колес:

,

.

По расчетным значениям выполнить эскизы конической шестерни и колес (рис.11).

Толщина обода ;

фаска f=(0,5....0,6)m_te;

ширина овода ₀ =2,5m_te+2;

толщина диска С=(0,35)b;

длина ступицы l_cт=(1....1,2)d_к;

диаметр ступицы d_ст=1,55d_к;

литейные уклоны 7; радиусы R=6 мм

Рис. 11. Эскиз конического колеса

7.1.2 Расчет сил в зацеплении (рис. 12).

Силы в зацеплении для колес с прямым зубом:

Рис.12. Силы в зацеплении

Окружная сила на среднем диаметре колеса

,

где d_m2= 0,857d_e2 – средний диаметр колеса.

Осевая сила на шестерни

,

где =20 –угол зацепления, tg 20=0,364.

Радиальная сила на шестерне

.

Осевая сила на колесе

F_a2=F_r1.

Силы в зацеплении для колес с круговым зубом:

Окружная сила на среднем диаметре колеса

,

где d_m2= 0,857d_e2 – средний диаметр колеса.

Осевая сила на колесе

F_a2=F_r1=F_t2(0,44 cos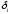– 0,7sin).

Радиальная сила на колесе

F_r2=F_a1=F_t2(0,44 sin + 0,7 cos).

7.1.3 Проверка зубьев колес по напряжениям изгиба.

Напряжения изгиба в зубьях колеса

.

Напряжение изгиба в зубьях шестерни

.

Значения коэффициентов Y_FS1и Y_FS2, учитывающих форму зуба и концентрацию напряжений.

Для колес изготовленных без смещения

Z 17 20 25 30 40 50 60 80 100 180

Y_F 4,27 4,07 3,9 3,8 3,7 3,65 3,63 3,61 3,6 3,62

Проверка зубьев колес по контактным напряжениям

,

где – выбирается по табл. 14.

Расчетное контактное напряжение лежит в интервале: