∆x = ∆X ; ∆y

= ∆Y .

2

2

Для рассматриваемого примера имеем

∆x = ∆X

= 2,4

=1,2 А; ∆y = ∆Y

=17,5

=8,57 ≈9 В.

2

2

2

2

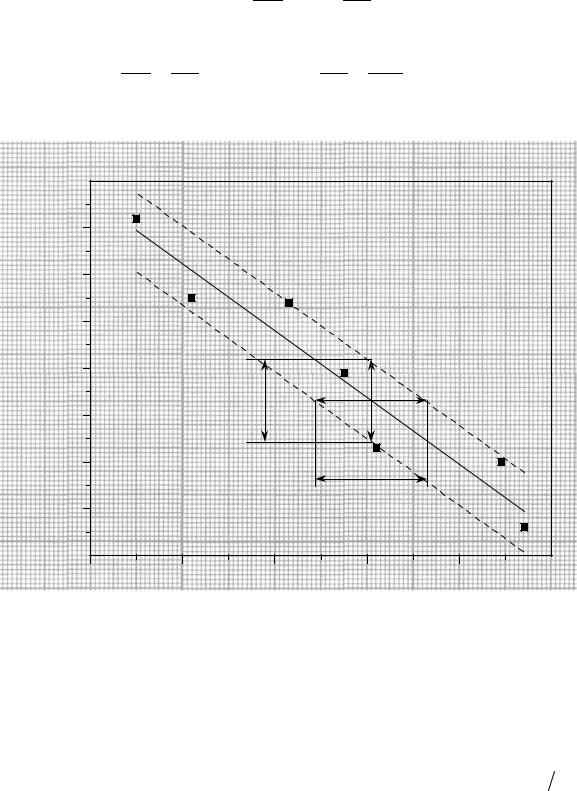
Относительные погрешности εx и εy оцениваем по формуле (3.1).

y, В

70

60

50

40

•C

30

∆Y

20

∆X

10

0

2

4

6

8

x, А

Рис. 9.2

9.5. Графическое дифференцирование

Графическое дифференцирование может понадобиться, напри-

мер, при вычислении дифференциального сопротивления Rd диода.

Вольт–амперная характеристика диода нелинейная, поэтому его со-

противление зависит от приложенного напряжения. Понятие статиче-

ского сопротивления (сопротивления постоянному току

R =U I ) в

данном случае лишено физического смысла, поэтому определяют

дифференциальное сопротивление Rd

при заданном напряжении. В

51

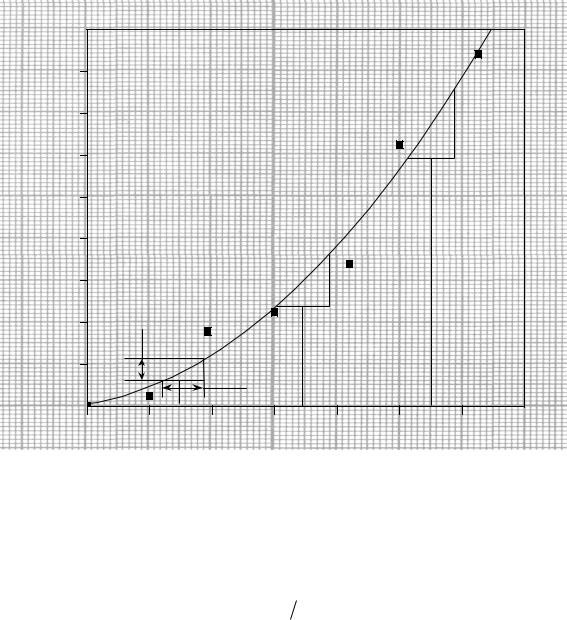
качестве примера рассмотрим экспериментальную вольт-амперную

характеристику

полупроводникового

диода,

представленную

на

рис. 9.3.

I, А

16

14

∆I3

12

∆U3

10

8

6

∆I2

4

∆U2

∆I1

2

∆U1

0

1 U1 2

3 U2 4

5 U3 6 U , В

Рис. 9.3

Величина

Rd

находится путем дифференцирования вольт-

амперной характеристики. Известно, что производная от функции

y(x) равна угловому коэффициенту касательной, построенной к кри-

вой y(x). Поэтому

после графического отображения эксперимен-

тальной кривой для вычисления dy dx в некоторой точке достаточно

провести на графике касательную в той же точке и вычислить ее уг-

ловой коэффициент. Однако, данный прием весьма чувствителен к

точности построения кривой – даже небольшая неточность, допу-

щенная при вычерчивании, может привести к ощутимым ошибкам в

расчетах.

По этой причине, при выполнении графического дифференци-

рования в рамках лабораторного практикума по физике применяется

следующий способ.

Вначале определяются значения аргументов, в

52